stron 17 (24.05.1995)
Spis treści
1. Wektory i rachunek wektorowy
2. Analiza wymiarowa
2.1. Zmiana wartości wielkości fizycznych wywołana zmianą jednostek miar
2.2. Rozwiązywanie zadań za pomocą analizy wymiarowej
2.2.1. Dynamika
2.2.2. Drgania i fale
2.2.3. Termodynamika
2.2.4. Elektromagnetyzm
2.2.5. Fizyka mikroświata
2.3. Naturalne układy jednostek miar
3. Inercyjne i nieinercyjne układy odniesienia
3.1.Kinematyka ruchu obrotowego
3.2. Siła Coriolisa
4. Pole grawitacyjne
4.1. Przyśpieszenie grawitacyjne
4.2. Energia potencjalna i potencjał grawitacyjny
4.3. Przyśpieszenie ziemskie
1. Wektory i rachunek
wektorowy
1.1. Dane są dwa wektory: a 3 i 4 j 2 k
i b 8 i 3 j 12 k . Obliczyć
a) sumę a b ,
b) różnicę a b ,
c) iloczyn skalarny a b ,
d) iloczyn wektorowy a b ,
e) wektory jednostkowe wzdłuż wektorów a i b
r
r
Ponadto rozłożyć wektor a na dwa wektory a p i a r takie, że a p jest prostopadłe do
b
wektora r , zaś a
r
jest
równoległe
do
wektora
.
b
r
1.2. Dany jest wektor r 7 i 3 j 12 k . Obliczyć:
a) długość tego wektora,
b) kąty, jaki tworzy on z osiami x, y i z
c) jego cosinusy kierunkowe.
1.3.
Obliczyć,
między
sobą
dwa
wektory
r
r jaki r kąt r tworzą
r
r
r
r
a 5 i 2 j 7 k i b 3 i 6 j 2 k .
r
1.4. Obliczyć współrzędne wektora a , prostopadłego do wektora b 2 i 3 j 5 k .
Założyć, że wektor ma długość 15, a jego składowa x-owa jest równa 2.
1.5. Jaki kąt tworzy wektor a 3 i 5 j 12 k z prostą leżącą w płaszczyźnie zy i
tworzącą z osią y kąt 35 ?
2. Analiza wymiarowa
Międynarodowy Układ Jednostek Miar SI
( Systeme International d'Unitees )
Układ jednostek to zbiór jednostek miar uznanych za podstawowe oraz innych jednostek,
które nazywa się pochodnymi, które przez te podstawowe się wyrażają. Tak np w układzie
międzynarodowym SI jednostki długości, czasu i masy są traktowane jako jednostki
podstawowe, natomiast jednostki siły, pędu i energii jako jednostki pochodne. Ta sama
wielkość fizyczna może być w jednym układzie jednostką podstawową, a w innym jednostką
pochodną. Jednostki pochodne tworzy się z jednostek podstawowych na podstawie praw
fizycznych wiążących rozpatrywane wielkości. Przykładowo, jednostka siły niuton jako
jednostka pochodna wyraża się poprzez jednostki podstawowe w postaci N=kgm/s2 dlatego,
że istnieje prawo fizyczne ( II zasada dynamiki Newtona ) wiążące rozpatrywane wielkości.
Istnieje możliwość utworzenia wielu układów jednostek miar, które różniłyby się ilością i
rodzajem podstawowych jednostek miar. Do pomyślenia jest zarówno układ, w którym byłaby
tylko jedna jednostka podstawowa (pozostałe byłyby pochodnymi, otrzymanymi za pomocą
praw fizycznych i wyrażonymi poprzez tą jedyną), jak i sytuacja odwrotna, gdy w układzie
występowałyby jedynie jednostki podstawowe. Praktyczna stosowalność układu nakłada
jednakże silne ograniczenia na ilość jednostek podstawowych.
Obowiązującym obecnie jest układ SI, bazujący na następujących siedmiu podstawowych
jednostkach miar (obok nazwa danej jednostki i jej skrót):
L - jednostka długości ;
metr - m
M - jednostka masy:
kilogram - kg
T - jednostka czasu:
sekunda - s
I - jednostka natężenia prądu:
amper - A
- jednostka temperatury termodynamicznej: kelwin - K
J - jednostka światłości:
kandela - cd
N - jednostka ilości materii.
mol - mol
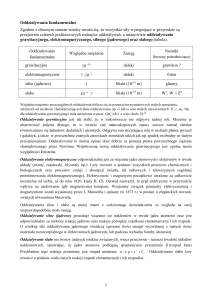
Każda wielkość fizyczna może być wyrażone jedynie poprzez te siedem jednostek miar.
Przykładowo dla energii E, współczynnika przewodnictwa cieplnego , pojemności
elektrycznej C i strumienia magnetycznego mamy w układzie SI następujące wyrażenia
wymiarowe:
[ E ] L M T
[ C ] L M T I
2
[ ] L M T
[ ] L M T I
2
2
1
4
3
2
2
2
1
1
Nawias kwadratowy informuje, ze rzecz dotyczy wymiaru wielkości, zaś wykładniki
potegowe informują o wymiarach danej wielkości względem odpowiednich jednostek miar.
Możemy zatem powiedzieć, że np. energia E ma wymiar 2 względem jednostki długości,
wymiar 1 względem jednostki masy i wymiar -2 względem jednostki czasu.
Jedną z zalet układu SI jest obecność w nim jednostek miar, które od dawna stosuje się w
praktyce. Wadą jest natomiast konieczność wprowadzenia dwu stałych - stałej elektrycznej 0
i stałej magnetycznej 0 - w celu dopasowania jednostek mechanicznych z
elektromagnetycznymi.
Zmiana wartości liczbowych wielkości fizycznych wywołana
zmianą podstawowych jednostek miar w danym układzie.
Zmiana wartości podstawowych jednostek miar powoduje zmianę wartości liczbowej
danej wielkości fizycznej. Przykładowo, w układzie SI, gdzie jednostką długości jest metr, a
czasu sekunda, wartość przyśpieszenia ziemskiego wynosi g=9,81. Jaka będzie ta wartość w
układzie, w którym za jednostkę długość uznamy np. cal, zaś za jednostkę czasu np. minutę ?
Spróbujmy rozwiązać zadanie przeliczania wartości z jednego układu jednostek miar do
drugiego w sposób ogólny.
Niech przykładowo wielkość fizyczna A wyraża się w następujący sposób poprzez
podstawowe jednostki miar tego układu
[ A ] L T M
p
r
s
(1)
gdzie L,T i M oznaczają, jak wyżej, uogólnione oznaczenia jednostki, odpowiednio,
długości, czasu i masy,
Jeżeli zmienimy (zwiększymy) w danym układzie jednostkę długości n1 razy, jednostkę
czasu n2 razy, jednostkę masy n3 razy, to wartość liczbowa danej wielkości ,zgodnie z (1)
zmieni się 1/k razy, gdzie
k ( n1 ) ( n2 ) ( n3 )
p
r
s
Powróćmy zatem dla naszego wcześniejszego przykładu. Ponieważ 1 cal=2,54 cm, zaś 1
minuta =60 sekund, to n1=2,54/100=0,0254 , natomiast n2=60/1. Dlatego
k 0,0254 60 7,05555 10
2
6
Zatem wartość przyśpieszenia ziemskiego w nowym układzie
9,81(1/k)=9,81141732,28=1390393,6668 cali/minutę, czyli g=1,39 Mcali/min.
wynosi
Analiza wymiarowa jako sposób rozwiązywania zadań
Równania wiążące wielkości fizyczne muszą mieć taką postać, aby wymiary występujące przy
odpowiednich podstawowych jednostkach miar po lewej i prawej strony danej równości były
takie same . Przykładowo, równanie wyrażające okres drgań wahadła matematycznego ma
postać:
l
2
g
(2)
gdzie jest okresem drgań, l jest długością wahadła, zaś g jest przyśpieszeniem
grawitacyjnym. Jak łatwo sprawdzić w równaniu (2), po odpowiednich przekształceniach, po
obiu stronach równości występuje jedynie czas w potędze pierwszej. Równanie (2)
przepiszmy w postaci
2l g
1/ 2
które w najogólniejszej formie można zapisać tak:
1/ 2
c l g
(3)
gdzie c=2, =1/2, =-1/2.
Analiza wymiarowa opiera się na założeniu, że tak jak w równaniu (3), dana wielkość
fizyczna może być przedstawiona jako jednomian potęgowy innych, zależnych wielkości
fizycznych. Niejednokrotnie daje się jednoznacznie wyznaczyć wykładniki potęgowe w
postulowanej równości typu (3). W jaki sposób działa ta metoda zostanie zademonstrowane
na przykładzie wyznaczenia okresu drgań wahadła matematycznego.
Etap I: wypisanie wielkości fizycznych, od których - jak przypuszczamy - może zależeć
okres drgań T. Niech będą to: m - masa kulki, l -długość nici , g - przyśpieszenie
grawitacyjne. Dwie pierwsze wielkości zostały wybrane dlatego, że charakteryzują one samo
wahadło, natomiast trzecia wielkość charakteryzuje pole grawitacyjne, bez którego nie byłoby
drgań. Mamy zatem N=4 wielkości, pomiędzy którymi szukamy związku (, m, l, g ) oraz
K=3 jednostki miar, przez które się one wyrażają ( L, T, M).
Etap II: Postulujemy następujący kształt równania wiążącego te cztery wielkości:
c l g m
(4)
W powyższym równaniu c jest liczbą, której wartości metoda analizy wymiarowej nie
potrafi wyznaczyć. Postulujemy, co znajduje uzasadnienie w wielu przykładach, że wartość c
zbliżona jest do jedyności.
Równanie (4) zapiszemy dla jednostek miar w następujący sposób:
2
(5)
T
L L T
M
Równanie (5) jest równoważne trzem równaniom, zapisanym dla każdej jednostki miary
oddzielnie:
T:
1 2
L:
0
M:
0
(6)
Zatem równania (6) wynikają z przyrównania wykładników potęgowych przy
odpowiednich jednostkach miar.
Rozwiązując (6) otrzymamy:
1
1
2
2
Ostatecznie równanie (4) będzie miało postać
c l g
1/ 2
1 / 2
0
m c
0
l
g
(7)
Otrzymaliśmy zatem równanie, które poprawnie oddaje funkcyjną zależność okresu drgań
od długości wahadła i przyśpieszenia grawitacyjnego.
Zauważmy, że układ równań (6) potrafiliśmy rozwiązać dlatego, że ilość równań była
równa ilości niewiadomych. Zatem, gdy ilość rozpatrywanych wielkości przewyższa o jeden
ilość wykładników potęgowych (N=K+1 ), to wartości tych ostatnich będzie można
wyznaczyć. Gdyby natomiast N>K+1, wtedy należałoby zrobić dodatkowe założenia
dotyczące rozpatrywanego problemu. Ilustruje to poniższy przykład.
W cylindrycznym naczyniu o polu przekroju poprzecznego S1 znajduje się ciecz
nielepka o gęstości , wypełniająca naczynie do wysokości h. W dnie naczynia znajduje
się otwór o powierzchni S2, przez który ciecz wypływa. Oszacować czas wypływu cieczy
z naczynia.
Ponieważ wypływ odbywa się pod wpływem siły ciężkości, dlatego czas wypływu oprócz wielkości występujących w treści zadania - będzie zależał od przyśpieszenia
grawitacyjnego g. Zatem
t c h g S S
1
2
(8)
Równanie to zapisane za pomocą jednostek miar przyjmie postać:
T M L 3 L L T 2 L2 L2
Jest to równoważne następującemu kładowi równań
T:
1 2
Jak łatwo sprawdzić
M:
0
L:
0 3 2 2
0
1 / 2
czyli czas wypływu nie zależy od gęstości. Trzech pozostałych wykładników nie można
obliczyć nie czyniąc dodatkowych założeń. Zróbmy więc następujące założenie: prędkość
wypływu nie zależy od powierzchni otworu. Oznacz to, że czas wypływu jest odwrotnie
proporcjonalny do powierzchni otworu S2 ( = 1 ), oraz że jest on wprost proporcjonalny do
ilości cieczy w naczyniu, co dla ustalonego h oznacza, że także do S1 ( =1 ). To założenie
umożliwia obliczenie ostatniego wykładnika. Dostajemy, że =1/2. Zatem ostatecznie
h S 1
t c
g S 2
Inny sposób umożliwiający zwiększenie ilości równań polega na tym, że zwieksza się
ilość jednostek miar, dodając jednostki pochodne. Rozpatrzmy poniższy przykład.
W cieczy o gęstości i współczynniku lepkości wypływa pęcherzyk zapełniony
gazem o pomijalnej gęstości i promieniu r. Jaka ustali się prędkość v wypływu tego
pęcherzyka ?
Ponieważ ruch pęcherzyka odbywa się w polu grawitacyjnym, to oprócz wielkości
wymienionych w zadaniu, rozpatrzyć także trzeba zależność prędkości od przyśpieszenia
grawitacyjne g. Zatem
v c r g
(9)
Równanie powyższe przepisane dla podstawowych jednostek miar przyjmie postać
1
2
3
1 1
(10)
LT
L LT M L M L
T
Jak łatwo zauważyć mamy cztery niewiadome wykładniki potęgowe i jedynie trzy
równania ( dla M, T, i L ) z których możemy je wyznaczyć.
Spróbujmy zwiększyć ilość równań wprowadzając dodatkową jednostkę miary - siłę.
Oznaczmy jednostkę tej miary jako F. Wtedy równanie (10) przybierze postać
LT
1
L
M
F M 1
TF L
L3
2
Rozpisując je dla poszczególnych jednostek miar dostaniemy
T: 1
M:
0
L:
1 3 2
F:
0
(11)
Rozwiązując układ (11) otrzymamy
2
1
1
1
Zatem dla prędkości wypływu pęcherzyka uzyskaliśmy następujące równanie
v
c gr
2
.
Analizę wymiarową można także stosować w zadaniach dotyczących modelowania
zjawisk. Modelowanie to zamiana badania interesującego nas zjawiska występującego w
naturze badaniem analogicznego zjawiska na modelu wykonanego w większej lub mniejszej
skali.. Rozpatrzymy jako przykład poniższe zadanie.
Śmigłowiec i jego model w skali 1:10 wykonane są z tych samych materiałów. Jaką
moc musi mieć silnik zdolny utrzymać w powietrzu śmigłowiec, jeżeli model
utrzymywany jest w powietrzu przez silnik o mocy Pm=10 W ?
Śmigłowiec utrzymuje się w powietrzu dzięki temu, że odrzuca w dół pewną masę
powietrza. Jeżeli w czasie t śmigło zakreśli powierzchnię S, nadając powietrzu prędkość v,
to uzyska ono pęd p równy
p=mv=Vv=Svtv=v2St
Zgodnie z trzecią zasadą dynamiki Newtona powietrze nada przeciwnie skierowany pęd
śmigłowcu. Zatem siła, z jaką powietrze działa na śmigłowiec jest równa
F=(pt)=v2S
Aby śmigłowiec utrzymał się w powietrzu, siła ta musi być równa sile grawitacji
działającej na niego
v2Sg
gdzie M jest masą śmigłowca. Z powyższego równania możemy wyznaczyć prędkość v
strumienia powietrza:
M g
v
S
Moc silnika śmigłowca obliczymy z równania P=Fv. Dlatego
M g 3
P=v3S=
S
Oznaczając indeksem m wielkości dotyczące modelu śmigłowca dostajemy
3
3
M Sm
V S
P
= m
Pm
Mm S
Vm S
Zwiększając n razy rozmiar L powodujemy zwiększenie powierzchni n2 razy oraz
zwiększenie objętości n3 razy. Dlatego
9
L Lm
P
1
n9 n7 / 2
Pm
n
Lm L
2
2
W naszym przypadku n=10. Dla wartości podanych w zadaniu
P=30107/2=94,868 kW.
Zadania
2.1. Zmiana wartości wielkości fizycznych wywołana zmianą jednostek miar
2.1.1. Obliczyć wartość stałej grawitacji G w takim układzie jednostek miar , w
którym jednostką masy jest masa Słońca ( Ms= 1,98891030kg), jednostką odległości jest
parsek (1 ps= 3,085677561016 m), zaś jednostką czasu jest jeden rok ( 1 rok = 31556925,97 s
).
2.1.2. Wartość ciepła właściwego miedzi, równą 0,038 J/(kgK) w układzie SI,
przetransformować do układu, w którym jednostką energii jest elektronowolt, a jednostką
masy jest atomowa jednostka masy.
2.1.3. Atmosfera fizyczna, pozaukładową jednostka ciśnienia, zdefiniowana jest jako
takie ciśnienie, które równoważne jest ciśnieniu słupa rtęci o gęstości 13,595 g/cm3 i o
wysokości 76 cm, w polu grawitacyjnym g=980,665 cm/s2 . Ilu paskalom odpowiada jedna
atmosfera?
2.1.4. Jaka jest równowartość w układzie SI nadal używanej pozaukładowej jednostki
mocy 1 kcal/godzinę ? Przyjąć, że 1 cal=4,1868 J.
2.1.5. W układzie SI jednostką modułu Younga jest paskal. Wartość modułu Younga
dla miedzi wynosi 121010 Pa. Jaka będzie ta wartość wyrażona w pozaukładowych
jednostkach kgs/mm2 ?. Wskazówka: 1 kgs=9,81 N.
2.1.6. Obliczyć, jaki będzie przelicznik pozwalający zamieniać jednostkę
współczynnika przewodnictwa cieplnego w układzie SI w pozaukładową jednostkę
kcal/(godzinam2K).
2.1.7. Jaki jest związek pomiędzy jednostką natężenia głosu w układzie SI a
pozaukładową jednostka erg/(cm2s) ?
2.1.8. Ile razy zmieniłaby się wartość liczbowa oporu elektrycznego pewnego metalu,
gdyby jednostkę długości zwiększyć 10 razy, jednostkę masy zmniejszyć 1000 razy, jednostkę
czasu zwiększyć 3600 razy, a jednostkę natężenia prądu zmniejszyć 100 razy.
2.1.9. Jednostka spektralnej gęstości strumienia energii przypadająca na jednostkową
długości fali wyraża się w układzie SI w W/m, zaś w układzie CGS w ergach/(scm). Jaki jest
współczynnik przeliczeniowy pomiędzy tymi układami ?
2.1.10. Wartość stałej Stefana-Boltzmanna w układzie SI wynosi 5,6710-8 W/(m2K4).
Jaka jest wartość tej stałej, wyrażonej w erg/(scm2K4) ?
2.2 Rozwiązywanie zadań za pomocą analizy wymiarowej
2.2.1. Dynamika
2.2.1.1. Satelita porusza się swobodnie wokół pewnej planety, w pobliżu jej
powierzchni. Oszacować jego prędkość orbitalną oraz okres obiegu planety. Obliczenia
wykonać dla Ziemi.
2.2.1.2. Oszacować przyśpieszenie grawitacyjne na powierzchni zadanej planety lub
gwiazdy. Obliczenia wykonać dla Ziemi i Słońca.
2.2.1.3. Oszacować czas swobodnego spadku ciała z pewnej wysokości na zadanej
planecie. Obliczenia wykonać dla Ziemi.
2.2.1.4. Oszacować czas swobodnego przelotu kamienia przez tunel przewiercony
wzdłuż średnicy Ziemi.
2.2.1.5. Oszacować ciśnienie panujące we wnętrzu ciała o dużych rozmiarach.
Obliczenia wykonać dla Ziemi i Słońca.
2.2.1.6. Otrzymać wyrażenie na siłę przyciągania grawitacyjnego dwu mas
punktowych oddalonych od siebie, zakładając, że wykładniki potęgowe przy obu masach mają
taką samą wartość.
2.2.1.7. Otrzymać wyrażenie na siłę przyciągania elektrycznego dwu ładunków
punktowych oddalonych od siebie, zakładając, że wykładniki potęgowe przy obu ładunkach
mają taką samą wartość.
2.2.1.8. Otrzymać wyrażenie na energię kinetyczną cząstki swobodnej o masie m i
prędkości v.
2.2.1.9. W gazowym ośrodku o gęstości porusza się ze stałą prędkością ciało o
poprzecznym rozmiarze R. Oszacować siłę oporu działającą na to ciało. Obliczenia wykonać
dla poruszającego się samochodu.
2.2.1.10. Siła Coriolisa działa na ciała poruszające się z pewną prędkością w układzie
odniesienia, który sam się obraca z zadaną prędkością kątową. Otrzymać wyrażenie na
wartość tej siły. Wykonać obliczenia dla samolotu poruszającego się nad równikiem
ziemskim.
2.2.1.11. Ciało o pewnej masie, zaczepione na końcu nici o zadanej długości, wiruje
dookoła ustalonej osi. Otrzymać wyrażenie na siłę naciągu nici.
2.2.1.12. Na ciało o pewnej masie działa na ustalonej drodze stała siła. Jaka będzie
prędkość i energia kinetyczna tego ciała na końcu tej drogi ?
2.2.1.13. Promień światła przebiegając w pobliżu dużej masy na skutek oddziaływania
grawitacyjnego zmienia nieco swój kierunek o kąt . Zakładając, że ugięcie to jest
proporcjonalne do stałej grawitacji, otrzymać wyrażenie na jego wielkość. Obliczenia
wykonać dla promienia przebiegającego w pobliżu powierzchni Słońca.
2.2.1.14. Czarna dziura jest obiektem, który powstaje w rezultacie grawitacyjnego
zapadania się gwiazdy lub galaktyki. Promień czarnej dziury określa się jako odległość od jej
centrum, gdzie prędkość ucieczki jest równa prędkości światła. Otrzymać wyrażenie na
promień grawitacyjny danego obiektu. Oszacować go dla Ziemi i dla Słońca.
2.2.1.15. W rurze o średnicy D płynie ciecz o współczynniku lepkości . Ruch cieczy
wywołany jest zadanym gradientem ciśnienia wzdłuż długości rury dp/dl. Otrzymać wyrażenie
na objętość cieczy Q, przepływającą przez tą rurę w jednostce czasu. Wskazówka: Jako
niezależne przyjć jednostki długości, czasu i lepkości.
2.2.1.16. Bezwymiarowa wielkość zwana stałą Reynoldsa R występuje wtedy, gdy
rozważamy ruch ciała o rozmiarze l, poruszającego się z prędkością v w cieczy o gęstości i
współczynniku lepkości . Otrzymać wyrażenie na tą stałą R.
2.2.1.17. Bezwymiarowy parametr hydrodynamiczny, zwany liczbą Strouhala, służy między innymi - do opisu efektywności pływania ryb. Ryby machają ogonami na boki w celu
wytworzenia wirów, które wywołują strumień o dużej efektywności napędowej. Wyprowadzić
wyrażenie na liczbę Strouhala wiedząc, że zależy ona od częstotliwości uderzeń ogona ryby,
szerokości strumienia wytworzonych wirów i prędkości ryby.
Uwaga: Prędkość ryby występuje w mianowniku. Pływanie jest najefektywniejsze, gdy liczba
Strouhala przyjmuje wartości w zakresie od 0,25 do 0,35.
2.2.1.18. Piłka o masie m, promieniu r i nadwyżce ciśnienia p nad ciśnieniem
zewnętrznym zderza się z betonową ścianą. Oszacować czas tego zderzenia. Przyjąć m=400 g,
r=10 cm, p=1 atm.
2.2.1.19. Rozważmy planetę składającą się z materiału mającego gęstości i granicę
wytrzymałości na siły ścinające m .Otrzymać wzór na minimalną wartość promienia Rm i
masy Mm planety, której kształt będzie kulisty. Obliczenia wykonać dla planet złożonych z
lodu (g/cm3, m=3 MPa), z granitu (g/cm3, m=100 MPa) i z żelaza (g/cm3,
m=1 GPa).
2.2.1.20. Mały meteoryt uderza w powierzchnię planety, tworząc krater o promieniu R.
Zakładając, że cała energia kinetyczna meteorytu Ek zostaje zużyta na rozdrobnienie materiału
planety (mającego gęstość i granicę wytrzymałości na ścinanie m ) z objętości krateru,
znaleźć związek pomiędzy tymi wielkościami.
2.2.1.21. Niewielki meteoryt o masie m uderza z prędkością v w powierzchnię planety,
zbudowanej z materiału o gęstości i granicy wytrzymałości na ścinanie m. W rezultacie
zderzenia tworzy się krater. Otrzymać wyrażenie na promień R tego krateru. Obliczenia
wykonać dla meteorytu o masie m=1000 kg spadającego z drugą prędkością kosmiczną
v=11,2 km/s na skały osadowe (m=10 MPa).
2.2.1.22. Jakiej energii trzeba użyć, aby na powierzchni planety o gęstości , gdzie
przyśpieszenie grawitacyjne jest równe g, wykopać dół o rozmiarze R ?
2.2.1.23. W wyniku uderzenia dużego meteorytu w powierzchnię planety powstaje
krater o promieniu R. Zakładając, że energia kinetyczna meteorytu zostaje zużyta głównie na
wyrzucenie skał z objętości krateru, otrzymać związek pomiędzy energią kinetyczną
meteorytu Ek a promieniem krateru R. Obliczenia wykonać dla meteorytu o masie m=50 mln
kg spadającego z drugą prędkością kosmiczną v=11,2 km/s na skały granitowe (=2,7 g/cm3)
na Ziemi.
2.2.1.24. Wiatrak o średnicy skrzydeł D znajduje sie w strumieniu powietrza o gęstości
, mającego prędkość v względem niego. Otrzymać wyrażenie na maksymalną moc energii,
która otrzymać można z tego wiatraka.
2.2.2. Drgania i fale
2.2.2.1. Otrzymać wyrażenie na okres drgań prostego wahadła matematycznego.
2.2.2.2. Otrzymać wyrażenie na okres drgań kuleczki zawieszonej na sprężynie.
2.2.2.3. W gazie o gęstości wybuchł pocisk, wyzwalając energię E. Otrzymać
czasową zależność r(t) rozchodzenia się czoła powstałej fali uderzeniowej.
2.2.2.4. W ośrodku sprężystym o gęstości i o module Younga E rozchodzą się fale
podłużne. Otrzymać wyrażenie na ich prędkość. Obliczenia wykonać dla żelaza.
2.2.2.5. W konkretnym gazie rozchodzą się fale dźwiękowe. Otrzymać wzór
wyrażający temperaturową zależność ich prędkości. Obliczyć prędkość fal dźwiękowych dla
powietrza w temperaturze pokojowej.
2.2.2.6. Sznur zaczepiony jest jednym końcem na stałe do ściany, zaś drugi jego
swobodny koniec naciągany jest siłą N. Poruszając swobodnym końcem w kierunku
pionowym wzbudzamy w sznurze fale biegnące. Oszacować ich prędkość.
2.2.2.7. Kropelka cieczy o napięciu powierzchniowym została początkowo
nieznacznie odkształcona od swojej formy sferycznej, a następnie pozostawiona swobodnie.
W rezultacie odkształcenia zaczeły się drgania jej kształtu. Oszacować ich okres.
2.2.2.8. Cefeidy to gwiazdy, które pulsują, zmieniając okresowo swoją jasność i
rozmiary. Otrzymać równanie na okres tych drgań, zakładając że jest on funkcją masy
gwiazdy, jej średniego promienia i stałej grawitacyjnej. Obliczenia wykonać dla gwiazdy
takiej jak Słońce.
2.2.2.9. Na powierzchni wody rozchodzą się krótkie fale kapilarne, czyli takie, w
których decydującą rolę odgrywa siła napięcia powierzchniowego wody. Otrzymać zależność
ich prędkości od długości fali. Obliczenia wykonać dla fal o długości =1 mm.
2.2.2.10. Na powierzchni wody rozchodzą się długie fale grawitacyjne, czyli takie, w
których decydującą rolę odgrywa siła grawitacyjna. Otrzymać zależność ich prędkości od
długości fali. Obliczenia wykonać dla fal o długości =1 m.
2.2.2.11. Próżnia charakteryzuje się przenikalnością elektryczną 0 i przenikalnością
magnetyczną 0 . Otrzymać równanie na prędkość fali elektromagnetycznej w próżni.
2.2.3. Termodynamika
2.2.3.1. Stan gazu doskonałego opisany jest przez trzy parametry: ciśnienie, objętość i
temperaturę. Otrzymać zależność pomiędzy tymi parametrami.
2.2.3.2. Otrzymać wyrażenie na prędkość ruch cząstki gazu, którego temperatura jest
równa T. Obliczenia wykonać dla molekuły azotu w powietrzu o temperaturze pokojowej.
2.2.3.3. Oszacować minimalny promień planety Rmin, która potrafi utrzymać atmosferę
złożoną z gazu o masie cząsteczkowej . Średnia gęstość planety wynosi , zaś temperatura
na jej powierzchni Tp. Obliczenia wykonać dla Ziemi.
2.2.3.4. Ściana o powierzchni S i grubości h, wykonana z materiału o współczynniku
przewodnictwa cieplnego k, oddziela dwa pomieszczenia, różniące się temperaturą T.
Otrzymać wyrażenie na moc strumienia ciepła płynącego przez tą ścianę.
2.2.4. Elektromagnetyzm
2.2.4.1.Wyrazić poprzez podstawowe jednostki miar przenikalność elektryczną próżni
0, występującą w prawie Coulomba.
2.2.4.2. Wyrazić poprzez podstawowe jednostki miar przenikalność magnetyczną
próżni 0, występującą w równaniu otrzymanym w zadaniu 2.11.
2.2.4.3. Oszacować energię zawartą w kondensatorze o zadanej pojemności, do
którego przyłożono konkretne napięcie.
2.2.4.4. Oszacować gęstość objętościową energii [energia/objętość] w miejscu, w
którym istnieje pole elektryczne o natężeniu E.
2.2.4.5. Oszacować gęstość objętościową energii [energia/objętość] w miejscu, w
którym istnieje pole magnetyczne o indukcji B.
2.2.4.6. Otrzymać wyrażenie na indukcję pola magnetycznego B wytworzonego w
odległości x od przewodnika w którym płynie prąd o natężeniu I.
2.2.4.7. Cząstka o pewnym ładunku elektrycznym krąży po orbicie kołowej ze stałą
prędkością w stałym polu magnetycznym. Oszacować promień orbity jej toru. Obliczenia
wykonać dla elektronu w polu B=10-4 T, mającego prędkość v=103 m/s.
`
2.2.4.8. Do opornika o oporze R przyłożono napięcie U, w wyniku czego płynie w nim
prąd o natężeniu I. Jaki jest związek pomiędzy tymi wielkościami ?
`
2.2.4.9. Jaki potencjał elektryczny istnieje w punkcie oddalonym o x od ładunku
punktowego q ?
2.2.4.10. Dwa nieskończone, prostoliniowe druty naładowane są ze stałą gęstością
liniową ładunkiem elektrycznym. Druty są ułożone prostopadle do siebie i najmniejsza
odległość pomiędzy nimi wynosi x. Jaka jest wartość siły działającej pomiędzy nimi ?
2.2.4.11. Punktowy ładunek elektryczny znajduje się w pewnej odległości od dużej
metalowej płyty. Oszacować wielkość siły oddziaływania tego ładunku z płytą.
2.2.5. Fizyka mikroświata
2.2.5.1. Prawo przesunięć Wiena wiąże temperaturę ciała doskonale czarnego T z
długością fali max , na której ciało promieniuje najintensywniej: maxT=b, gdzie b jest stałą
Wiena. Obliczyć wartość tej stałej, jeżeli wiadomo, że jest ona funkcją stałych
fundamentalnych h, c i k, oraz że współczynnik liczbowy jest równy 1/5.
2.2.5.2. Prawo Stefana-Boltzmanna wiąże temperaturę ciała doskonale czarnego T z
całkowitą mocą W emitowanego promieniowania z jednostki jego powierzchni i ma postać
4
W T
gdzie jest stałą Stefana-Boltzmanna. Obliczyć wartość tej stałej, jeżeli wiadomo, że jest ona
funkcją stałych fundamentalnych h, c i k, oraz że współczynnik liczbowy jest równy 0,1645.
2.2.5.3. Elektron krąży po orbicie wokół jądra atomowego, przyciągany siłą
elektryczną. Zakładając, że ruch elektronu jest kwantowy i nierelatywistyczny, otrzymać
wyrażenie na promień jego orbity oraz wyrażenie na jego całkowitą energię. Obliczyć
promień orbity oraz energię dla atomu wodoru.
2.2.5.4. Molekuła liniowa o masie m i długości l obraca się wokół swojej osi symetrii.
Otrzymać wyrażenie na energię tego ruchu, zakładając że jest on kwantowy i
nierelatywistyczny. Obliczyć tą energię dla molekuły N2.
2.2.5.5. Otrzymać wyrażenie na energię fotonu, którego długość fali jest znana.
Foton jest cząstką kwantową i relatywistyczną. Obliczenia liczbowe wykonać dla fotonu o
=500 nm.
2.3. Naturalne układy jednostek miar
2.3.1. Z fundamentalnych stałych fizycznych:
c - prędkość światła, h - stała Planck'a,
G - stała grawitacji
metodą analizy wymiarowej utworzyć wielkości fizyczne o wymiarze długości, czasu i masy.
Obliczyć wartość tych wielkości.
2.3.2. Z fundamentalnych stałych fizycznych:
c - prędkość światła, h - stała Planck'a,
me - masa elektronu
metodą analizy wymiarowej utworzyć wielkości fizyczne o wymiarze długości, czasu i masy.
Obliczyć wartość tych wielkości.
2.3.3. Z fundamentalnych stałych fizycznych:
me - masa elektronu, h - stała Planck'a,
qe - ładunek elektronu
oraz ze stałej elektrycznej 0, metodą analizy wymiarowej utworzyć wielkości fizyczne o
wymiarze długości, czasu i energii. Obliczyć wartość tych wielkości.
3.1. Ruch obrotowy
3.1.1 Dzięki wpływowi Księżyca prędkość kątowa ruch wirowego Ziemi maleje w
ciągu jednego roku o k=210-10 swojej aktualnej wartości. Jak będzie długość doby za t=1 mld
lat ?
3.1.2 Pulsar w mgławicy Krab to gwiazda o promieni r=10 km, wykonująca bardzo
szybki ruch obrotowy o okresie T=33 ms.
a) Jaka jest prędkość kątowa tego pulsara ?
b) Jaka jest prędkość linowa punktu na jego równiku ?
Okres obrotu tego pulsara ulega bardzo powolnemu zwiększeniu w tempie n=4,310-13
sekundy w czasie jednej sekundy.
c) Jaka jest wartość opóźnienia kątowego tego pulsara ?
d) W jakim czasie jego okres zmaleje o m=1 % ?
3.1.1 Punkt rozpoczyna w chwili t=0, z zerową prędkością ruch po okręgu o
promieniu r=35 cm. Przyśpieszenie tangencjalne punktu jest stałe w czasie i wynosi at=0,1
m/s2.
a) Jaką prędkość linową i przyśpieszenie dośrodkowe ma to ciało po wykonaniu
jednego obiegu okręgu ?
b) W jakiej chwili czasu wartość przyśpieszenia dośrodkowego jest równa wartości
przyśpieszenia tangencjalnego ?
c) W jakiej chwili czasu kąt pomiędzy wektorem przyśpieszenia tangencjalnego i
wektorem przyśpieszenia całkowitego jest równy =30 ?
d) Jaka jest wartość całkowitego przyśpieszenia punktu po wykonaniu k=5 obiegów
okręgu ?
3.1.2 Punkt porusza się ze stałą wartością prędkości v=1 m/s wzdłuż sinusoidy danej
równaniem y=Asin(b x), gdzie A=1 [m], b=2 [m-1].
a) W jakim czasie punkt przebędzie z punktu (0,0) do punktu (1,0) ?
b) Jaka jest największa wartość przyśpieszenia dośrodkowego w ruchu tego punktu ?
Uwaga: Mając krzywa y=y(x) jej długość s i promień krzywizny R dane są równaniami:
L
Fdy I O
1 G JP
M
M Hdx KP
Q
R N
2
Fdy I
s z1 G Jdx
Hdx K
2
3/ 2
d2y
dx 2
U nas s[0,1]=5.38368
3.1.3 Talerz adaptera o średnicy d=20 cm obraca się ruchem jednostajnym, wykonując
n=33 obrotów na minutę.
a) Jaka jest prędkość kątowa talerza ?
b) Jaka jest prędkość liniowa punktu na brzegu talerza ?
c) Jakie jest przyśpieszenie dośrodkowe punktu na brzegu talerza ?
d) Jaka musiałaby być prędkość obrotowa talerza (w obr./min.), aby przyśpieszenie
dośrodkowe punktu na brzegu talerza było równe g=9,81 m/s2 ?
3.1.4 Talerz adaptera o średnicy d=20 cm obraca się ruchem jednostajnym, wykonując
n=45 obrotów na minutę. Gdy adapter wyłączono, talerz zatrzymał się po =15 sekundach.
Zakładając, że siła tarcia była stała w czasie, obliczyć:
a) przyśpieszenie kątowe talerza;
b) ilość wykonanych obrotów do momentu zatrzymania się talerza;
c) prędkość kątową talerza w chwili czasu t1=/2;
d) przyśpieszenie dośrodkowe punktu na brzegu talerza w chwili t1.
3.1.5 Obliczyć przyśpieszenie dośrodkowe ciała spoczywającego na:
a) równiku Ziemi;
b) w Szczecinie.
3.1.6 Jaka byłaby długość doby, gdyby wartość przyśpieszenia dośrodkowego na
równiku Ziemi była równa a=9,8 m/s2.
3.2. Siła Coriolisa
Szerokość geograficzna Szczecina =5324'.
3.2.1 Samolot o masie m=5104 kg leci nad równikiem, ze wschodu na zachód, z
prędkością v=1300 km/godz. Jaka jest wartość siły Coriolisa działającej na ten samolot i jak
jest ona skierowana ? Z jaką prędkością powinien poruszać się ten samolot, aby sumaryczna
siła bezwładności ( odśrodkowa i Coriolisa ) w układzie Ziemi była równa zero ?
3.2.2 Ciało spada swobodnie na równiku z pewnej wysokości, z zerową prędkością
początkową. Z jakiej wysokości spadło to ciało, jeżeli na powierzchni Ziemi jego odchylenie
od pionu wyniosło l=3 m ?
3.2.3 O ile odchyli się od pionu i w jaką stronę ciało spadające swobodnie z wysokości
h=30 m w Szczecinie ?
3.2.4 Samochód o masie 1200 kg porusza się z południa na północ ze stała prędkością
v=130 km/godz. na szerokości geograficznej Szczecina. Jaka jest wartość oraz kierunek siły
Coriolisa działającej na ten samochód ? Jaki jest stosunek wartości tej siły do siły
odśrodkowej wynikającej z ruchu wirowego Ziemi ?
3.2.5 Pojazd o masie m=1500 kg porusza się z prędkością v=100 km/godz. z zachodu
na wschód na szerokości geograficznej =45. O ile procent zmieni się ciężar tego pojazdu
skutkiem działania siły Coriolisa ?
3.2.6 Z jaką prędkością i w jaką stronę musi poruszać się ciało wzdłuż równika, aby
jego ciężar zwiększył się o 1 % skutkiem działania siły Coriolisa ? W jakim czasie ciało to
obiegnie Ziemię ?
3.2.7 Odra płynie w Szczecinie z południa na północ. Przyjmując, że prędkość wody w
rzece wynosi v=2 m/s, a szerokość rzeki l=100 m, obliczyć, o ile jest wyższy poziom wody na
jednym jej brzegu (którym ?) w porównani z drugim brzegiem.
3.2.8 Obliczyć pionową składową siły Coriolisa działającą na człowieka o masie m=70
kg, poruszającego się z prędkością v'=30 km/godz. w Szczecinie z zachodu na wschód.
3.2.9 Z jaką prędkością i w jakim kierunku musi poruszać się w płaszczyżnie
horyzontalnej ciało w Szczecinie, aby jego ciężar zmalał o k=0.04 % skutkiem działania siły
Coriolisa ?
3.2.10 Pocisk artyleryjski ma trafić w cel odległy o l=15 km, na szerokości
geograficznej Szczecina. Zakładając, że tor pocisku jest linią prostą, leżącą w płaszczyżnie
horyzontalnej i że pocisk ma stałą prędkość v=800 m/s, obliczyć, o ile odczyli się on z tego
toru u celu w rezultacie działania siły Coriolisa. Czy wielkość tego odchylenia zależy od
kierunku wystrzału ?
3.2.11 Niewielki statek o masie całkowitej M=2104 kg stoi nieruchomo na wodach
równikowych. Jaka będzie prędkość tego statku, gdy kotwicę o masie m=500 kg wciągnięto
na maszt o wysokości h=15 m ?
3.2.12 Płaski horyzontalny dysk obraca się ze stałą prędkością kątową =2 rad/s
wokół osi przechodzącej przez jego środek. Człowiek o masie m=70 kg porusza się ze stałą
względem dysku prędkością v'=2 m/s wzdłuż promienia dysku. W jakiej odległości od osi
dysku znajduje się człowiek, gdy dysk działa na niego siłą F=4103 N ?
3.2.13. Ciężarek zawieszony na lince o długości l=30 m wykonuje wahania o
amplitudzie a=2 m, zaznaczając w chwili maksymalnego wychylenia swoje położenie na
horyzontalnym kole. Zakładając, że wahadło to zawieszone jest w Szczecinie, obliczyć:
a) okres drgań tego wahadła;
b) okres obrotu jego płaszczyzny wahań;
c) odległość pomiędzy dwoma sąsiednimi znaczkami na poziomym kole.
4. Pole grawitacyjne
Stałe:
G=6,67210-11
Z-Ziemia, K-Księżyc, S-Słońce
lzs=1,495981011 m lzk=3,8475108 m.
Mk=Mz/81,3 Ms=1,998911030 kg Rs=6,95108 m
m3kg-1s-2
Rz=6,371106 m
Mz =5,981024 kg
4.1. Przyśpieszenie grawitacyjne
4.1.1. Traktując Ziemię jako jednorodną kulę, obliczyć wartość przyśpieszenia
grawitacyjnego g :
a) w środku Ziemi; b) na głębokości równej połowie promienia Ziemi;
c) na orbicie satelity krążącego na wysokości h=300 km nad Ziemią;
d) na orbicie satelity stacjonarnego; e) na orbicie Księżyca.
4.1.2. Obliczyć wartość przyśpieszenia grawitacyjnego wywołanego Słońcem:
a) na powierzchni Słońca,
b) na orbicie Ziemi.
W jakiej odległości od Słońca wartość tego przyśpieszenia wynosi 9,81 m/s2 ?
4.1.3. Na powierzchni planety o promieniu r=1000 km wartość przyśpieszenia
grawitacyjnego wynosi g=2 m/s2. Jaka jest średnia gęstość tej planety ? W jakiej odległości od
jej powierzchni wartość przyśpieszenia grawitacyjnego wynosi g=1 m/s2 ?
4.1.4. Jaki byłby okres sekundowego wahadła matematycznego sporządzonego na
Księżycu i przeniesionego na Ziemię ?
4.1.5. Jeden z dwóch takich samych zegarów wahadłowych został na okres jednej
doby przeniesiony na wysokość h=20 km nad powierzchnię Ziemi. Jaką różnicę czasu pokażą
te dwa zegary po ich ponownym spotkaniu ?
4.1.6. Obliczyć różnicę przyśpieszeń grawitacyjnych wywołanych
a) Księżycem, b) Słońcem
na dwu przeciwległych krańcach Ziemi (najbliższym i najdalszym od danego ciała).
4.1.7. Obliczyć różnicę przyśpieszeń grawitacyjnych wywołanych
a) Ziemią,
b) Słońcem
na dwu przeciwległych krańcach Księżyca (najbliższym i najdalszym od danego ciała).
4.1.8. Eksperymentator posiada aparaturę do pomiaru przyśpieszenia grawitacyjnego,
pozwalającą wyznaczyć wartość g z dokładnością do 0,01 m/s2. Na jaką wysokość nad
powierzchnię Ziemi musiałby wznieść tą aparaturę, aby zauważyć zmianę wartości
przyśpieszenia grawitacyjnego ? Na jaką głębokość pod powierzchnię Ziemi musiałby opuścić
tą aparaturę, aby zauważyć zmianę wartości przyśpieszenia grawitacyjnego ?
4.1.9. Planeta składa się z dwu jednorodnych warstw: kulistej warstwy wewnętrznej o
promieniu r1=2000 km i gęstości 1=7000 kg/m3 oraz warstwy zewnętrznej o grubości
r2=5000 km i gęstości 2=4000 kg/m3. Obliczyć wartość przyśpieszenia grawitacyjnego w
punktach odległych od środka planety o a) 1000 km, b) 3000 km, c) 7000 km, d) 9000 km.
4.1.10. Planeta o promieniu R=5000 km składa się z dwu jednorodnych warstw:
kulistej warstwy wewnętrznej o gęstości 1=7000 kg/m3 oraz warstwy zewnętrznej o gęstości
2=4000 kg/m3. Jaka jest grubość warstwy wewnętrznej, gdy wiadomo, że wartość
przyśpieszenia grawitacyjnego na jej powierzchni wynosi g=6 m/s2.
4.1.11. Rozpatrzmy układ Ziemia-Księżyc. Znaleźć położenie punktu, w którym
przyśpieszenie grawitacyjne od Ziemi i od Księżyca ma wartość g=0,1 m/s2. Jaka jest wartość
sumarycznego przyśpieszenia grawitacyjnego w tym punkcie i jaki kąt tworzy ten wektor z
kierunkiem ku Ziemi ?
4.1.12. Obliczyć wartość przyśpieszenia grawitacyjnego w punkcie równoodległym od
Ziemi i Księżyca, tworzącym z tymi obu ciałami trójkąt równoboczny.
4.1.13. Na powierzchni jednorodnej planety o promieniu R=6000 km i średniej
gęstości =5000 kg/m3 powstała stożkowa góra o wysokośći h=10 km i promierniu podstawy
r=50 km. Zakładając taką samą gęstość materiału góry jak i planety, oszacować wpływ góry
na wartość i kierunek wektora przyśpieszenia grawitacyjnego w punkcie znajdującym się na
powierzchni planety: a) u podnóża góry ; b) w odległości x=500 km od niej.
4.1.14. Tuż pod powierzchnią ziemi (średnia gęstość gruntu =3 g/cm3) powstała
pusta kulista wnęka o promieniu r=200 m. Jak i o ile zmieni się wartość przyśpieszenia
grawitacyjnego na powierzchni ziemi w punkcie nad tą wnęką ?
4.2. Energia potencjana i potencjał grawitacyjny
4.2.1. Ciało o masie m=70 kg znajduje się na powierzchni Ziemi. Obliczyć wartość
energii potencjalnej tego ciała i wartość potencjału grawitacyjnego w tym punkcie .
4.2.2. Ciało o masie m=70 kg spada swobodnie w tunelu z powierzchni Ziemi do jej
środka. O ile zmieni się jego energia potencjalna ? Jaka będzie jego prędkość w środku Ziemi,
gdy na powierzchni była równa zero ?
4.2.3. Dla jednorodnej planety o gęstości i promieniu R sporządzić wykresy
zależności przyśpieszenia grawitacyjnego i potencjału grawitacyjnego w funkcji promienia
wodzącego r, dla r od 0 do . Jaka jest wartość potencjału grawitacyjnego na powierzchni
planety i w jej środku ?
4.2.4. Rozpatrzmy jednorodną planetę o promieniu R i masie M. O jaką część jej
promienia należałoby się wznieść pewne ciało ponad jej powierzchnię, aby energia
potencjalna tego ciała wzrosła o 0,5 % ? O jaką część jej promienia należałoby zagłębić do jej
wnętrza pewne ciało, aby energia potencjalna tego ciała zmalała o 0,5 % ?
4.2.5. Ciało spada na powierzchnie Ziemi z wysokości h=30 km (brak oporu
powietrza). Jaka będzie prędkość tego ciała w chwili zderzenia z Ziemią ?
4.2.6. Ciało zostało wyrzucone pionowo do góry z powierzchni Ziemi z prędkością v=
10 km/s (brak oporu powietrza). Na jaką wysokość wzniesie się to ciało ?
4.2.7. Z jaką najmniejszą prędkością należałoby wyrzucić z Ziemi ciało, aby doleciało
ono na Księżyc ? A z jaką prędkością należałoby wyrzucić ciało z Księżyca, aby doleciało
ono do Ziemi ?
4.2.8. Druga prędkość kosmiczna na pewnej planecie o promieniu R=4000 km wynosi
v2=5 km/s. Jakie jest przyśpieszenie grawitacyjne na wysokości h=1000 km nad jej
powierzchnią ?
4.2.9. Satelita o masie m=500 kg i przekroju poprzecznym S=3 m2 obiega Ziemię po
orbicie kołowej, na wysokości h=250 km nad jej powierzchnią. Na tej wysokości gęstość
atmosfery wynosi =10-11 kg/m3.
a) Jaka siła tarcia działa na tego satelitę ? (Uwaga: zderzenia cząstek
atmosfery z satelitą ropatrywać jako całkowicie niesprężyste)
b) Ile wynosi całkowita energia satelity ?
c) O ile zmieni się ta energia w czasie jednego obiegu orbity ?
d) O ile zmaleje promień orbity w czasie jednego obiegu ?
e) O ile zmieni się prędkość w czasie jednego obiegu ?
4.3. Przyśpieszenie ziemskie
4.3.1. Wartość przyśpieszenia ziemskiego na powierzchni Ziemi, w punkcie o
szerokości geograficznej dobrze opisuje następujące wyrażenie: g()=9.7805+0,0517sin2
[m/s2].
a) Obliczyć wartość przyśpieszenia ziemskiego w Szczecinie (=5324');
b) obliczyć szerokość geograficzną, na której wartość g jest średnią
arytmetyczną dla równika i bieguna ziemskiego.
4.3.2. Obliczyć wartość przyśpieszenia odśrodkowego i jego stosunek do
przyśpieszenia grawitacyjnego dla punktu
a) na równiku Ziemi, b) na szerokości geograficznej Szczecina (=5324').
4.3.3. Znając okres obiegu Księżyca wokół Ziemi (Tk=27,3217 doby) oraz masy
Ziemi Mz i Księżyca Mk, obliczyć wartość siły dośrodkowej działającej na Księżyc.
4.3.4. Jaki kąt tworzy wektor przyśpieszenia ziemskiego z kierunkiem do środka
Ziemi w Szczecinie (=5324') ?
4.3.5. Jaki byłby kąt pomiędzy wektorem przyśpieszenia ziemskiego a kierunkiem do
środka Ziemii w Szczecinie (=5324') , gdyby doba na Ziemi trwała T=10 godzin? Jakie
byłoby wtedy przyśpieszenie ziemskie w Szczecinie ?
4.3.6. Jak długo trwałaby doba na Ziemi, gdyby przyśpieszenie ziemskie na równiku
było o 10 % mniejsze niż na biegunie Ziemii ?
4.3.7. Kulista planeta o promieniu R=3000 km ma średnią gęstość =3 g/cm3.
Zakładając, że długość doby na tej planecie wynosi T=10 godzin, obliczyć, o ile procent różni
się przyśpieszenie spadku swobodnego na równiku od przyśpieszenia na biegunie.
4.3.8. Zegar wahadłowy, prawidłowo chodzący na równiku ziemskim, został
przeniesiony na biegun ziemski. Jak będzie chodził tam ten zegar i jaka będzie różnica czasu
po jednej dobie z prawidłowo chodzącym zegarem na biegunie ?
4.3.9. Jeden z dwu takich samych zegarów wahadłowych znajdujących się na równiku
ziemskim został zabrany do samolotu, który obleciał z nim Ziemię wzdłuż równika w
kierunku zachodnim. Zakładając, że lot odbywał się ze stałą prędkością i trwał dokładnie
jedną dobę (na zegarze spoczywającym), obliczyć jaki czas wskaże zegar ruchomy, gdy
zegary ponownie się spotkają.