Piotr Posmykiewicz – Wykład z fizyki
1
Wykład 21
Wybrane zagadnienia z optyki geometrycznej.
21.1 Podstawowe prawa optyki. Całkowite wewnętrzne odbicie.
Jeszcze przed odkryciem natury światła znane
były
podstawowe
prostoliniowego
ośrodku
prawa
optyki:
rozchodzenia
optycznie
się
prawo
światła
jednorodnym,
Promień padający
w
prawo
θa
niezależności wiązek świetlnych (prawdziwe tylko
Normalna
θo
θb
w optyce liniowej), prawo odbicia światła i prawo
załamania światła.
Prawo
światła:
Promień odbity
prostoliniowego
światło
w
rozchodzenia
ośrodkach
się
jednorodnych rozprzestrzenia się po linii prostej.
Dowodem
na
to
jest
a
optycznie
obecnośd
b
Rysunek 21.1
cieni
pochodzących od przedmiotów oświetlanych źródłami o małych rozmiarach. Dokładne
doświadczenia pokazały jednak, że prawo to jest naruszone, jeżeli światło przechodzi przez
małe otwory, przy czym odchylenie od linii prostej jest tym większe im mniejszy otwór.
Prawo niezależności wiązek świetlnych: skutek wywołany pojedynczą wiązką nie zależy
od tego, czy pozostałe wiązki działają, czy też są usunięte. Rozbijając strumieo świetlny na
oddzielne wiązki światła (na przykład za pomocą przesłon), można wykazad, że działanie
wydzielonych wiązek jest niezależne.
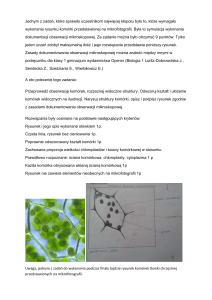
Jeżeli światło pada na granicę dwóch ośrodków (dwóch przezroczystych substancji), to
promieo padający (Rysunek 21.1) rozdziela się na dwa promienie – odbity i załamany,
których kierunki określone są prawem odbicia i załamania.
Prawo odbicia: promieo padający, odbity i normalna do powierzchni w punkcie odbicia
leżą w jednej płaszczyźnie, a kąt odbicia θo jest równy kątowi padania θa:
𝛉 𝐨 = 𝛉𝐚
21.1
Prawo odbicia.
Prawo załamania: promieo padający, załamany i normalna do powierzchni w punkcie
załamania leżą w jednej płaszczyźnie, a stosunek sinusa kąta padania θa do sinusa kąta
załamania θb jest stały dla danych ośrodków:
Piotr Posmykiewicz – Wykład z fizyki
sin θ a
sin θ b
2
= nb/a ,
21.2
Prawo załamania – Snella.
gdzie na/b – względny współczynnik załamania ośrodka a względem ośrodka b.
Względny współczynnik załamania dwóch ośrodków jest równy stosunkowi
bezwzględnych współczynników załamania (lub prościej – współczynników załamania) –
współczynników załamania ośrodków względem próżni:
𝐧𝐛
𝐚
𝐧
= 𝐧𝐛
𝐚
21.3
Uwzględniając 21.3 i 21.2 prawo załamania można zapisad w postaci
𝐧𝐚 𝐬𝐢𝐧𝛉𝐚 = 𝐧𝐛 𝐬𝐢𝐧𝛉𝐛
21.4
Prawo załamania – Snella.
Bezwzględny współczynnik załamania światła danego ośrodka zdefiniowany jest jako
stosunek prędkości światła w próżni do prędkości światła w tym ośrodku.
𝐜
𝐧=𝐯
21.5
Bezwzględny współczynnik załamania.
Światło zawsze porusza się wolniej w ośrodku innym niż próżnia. Oczywiście dla próżni n = 1.
Z dobrym przybliżeniem można przyjąd, że współczynnik załamania światła powietrz również
wynosi jeden.
Jeżeli światło przechodzi z jednego ośrodka do drugiego, to częstośd światła nie ulega
zmianie. W związku z tym c = λ0f i v = λf, gdzie λ0 i λ długości fal odpowiednio w próżni i w
danym ośrodku, a f jest
częstotliwością. Podstawiając powyższe zależności do 21.5
otrzymujemy:
𝐧=
𝛌𝟎
𝛌
21.6
Bezwzględny współczynnik załamania.
Z symetrii wyrażenia 21.4, wynika odwracalnośd biegu promieni świetlnych. Jeżeli
odwrócid bieg promienia b i zmusid go do padania na granicę dwóch ośrodków pod kątem θb,
to promieo załamany w ośrodku a będzie poruszad się pod kątem θa tzn. pokryje się z
promieniem padającym w ośrodku a.
Piotr Posmykiewicz – Wykład z fizyki
3
Równania 21.2 i 21.4 pokazują, że jeżeli drugi ośrodek (b) ma mniejszy współczynnik
załamania (nb < na) tak jak na rysunku 21.1, wtedy promienie załamane odchylają się bardziej
od normalnej. To tłumaczy dlaczego zanurzony w wodzie patyk, czy słomka do picia wydają
się zagięte; światło biegnące z pod powierzchni zmienia swój kierunek na granicy woda –
powietrze i dlatego promieo wydaje się wychodzid z punktu powyżej rzeczywistego miejsca
(Rysunek 21.2).
nb (powietrze) = 1
Pozorny koniec
linijki
na (woda) = 1,33
Rzeczywisty
koniec linijki
a.
b.
Rysunek 21.2
Jak pokazuje rysunek 21.3 wraz ze zwiększaniem kąta padania w ośrodku gęstszym, kąt
załamania wzrasta. W tym przypadku równanie Snella możemy przepisad w postaci:
n
sinθb = n a sinθa
b
Ponieważ na > nb. to będzie istniał taki kąt
b
θa = θgr dla którego sinθb będzie równy
1
jeden, a tym samym θb = 900, czyli promieo
załamie się pod kątem prostym. Jeżeli kąt
padania θa > θgr, wtedy żaden promieo
2
θb
θb=900
nb
na
padający nie będzie się mógł wydostad z
θa
θgr
θa > θgr
danego ośrodka i nastąpi tzw. całkowite
wewnętrzne odbicie. Należy pamiętad, że
zjawisko to będzie zachodzid tylko wtedy,
gdy
drugi ośrodek
ma
3
4
a
P
Rysunek 21.3
współczynnik
załamania mniejszy od pierwszego.
Jako przykład weźmy pod uwagę szkło i powietrze (na = nsz = 1,52, nb = npow = 1):
1
sinθgr = 1,52 sin900 = 0,658
θgr = 41, 10
Jak widad światło rozprzestrzeniające się w szkle i padające na granicę szkło – powietrze
zostanie całkowicie wewnętrznie odbite, jeżeli będzie padad pod kątem 41.1 0 lub większym.
Piotr Posmykiewicz – Wykład z fizyki
4
Dlatego też do całkowitego odbicia światła można używad pryzmatów , które mają kąty 450 450 - 900 lub większe. Pryzmaty są pod pewnym względem lepsze od zwykłych odbijających
metalowych powierzchni, takich jakie są używane w zwykłych lustrach. Przede wszystkim
żadne lustro nie odbija światła w 100% tak jak to robi pryzmat. Poza tym pryzmaty mają tę
przewagę nad zwykłym zwierciadłem, że są trwałe i
nie tracą połysku.
Na rysunku 21.4a przedstawiony jest pryzmat
zwany pryzmatem Porro. Światło wchodzi i
wychodzi
pod
kątem
prostym
Pryzmaty
Porro
do
przeciwprostokątnej i jest całkowicie odbijane od
przyprostokątnych. W rezultacie następuje zmiana
kierunku rozchodzenia się światła o 1800. W
lornetkach często stosuje się układ dwóch
pryzmatów Porro, tak jak przedstawia to rysunek
21.4b.
b
a
Brylant zawdzięcza swój blask w dużej mierze
Rysunek 21.4
temu, iż posiada duży współczynnik załamania
światła (n = 2,417), a tym samym odpowiadający mu duży kąt graniczny. Światło wpadające
do oszlifowanego diamentu odbija się całkowicie od strony wewnętrznej ścian i następnie
wychodzi z przedniej ściany.
Jeżeli promieo wpada do przezroczystego przewodu (Rysunek 21.5) i współczynnik
załamania
materiału
jest
większy
od
współczynnika załamania otoczenie, wtedy
promieo
może
wewnętrznych
„uwięzione”
doświadczad
odbid.
w
całkowitych
Światło
przewodzie
nawet
zostaje
jeżeli
Pojedyncze
włókno optyczne
Wiązka
światłowodowa
przewód jest wygięty. Takie przewody nazywa
się czasami światłowodami. Wiązka włókien
Rysunek 21.5
szklanych lub plastikowych zachowuje się w ten sam sposób i dodatkowo jest elastyczna.
Taka wiązka może składad się z tysięcy pojedynczych włókien o grubościach od 0,002 do
0.01mm. Za pomocą takich wiązek można przekazywad obraz na odległośd jak widad to na
rysunku 21.6. Tego typu światłowody znalazły szerokie zastosowanie w urządzeniach
Piotr Posmykiewicz – Wykład z fizyki
5
zwanych endoskopami wprowadzanymi do różnych części ciała w celach diagnostycznych lub
wykonywania mikrooperacji (laparoskopia).
Włókna optyczne znajdują zastosowania również w światłowodach w systemach
telekomunikacji, przez które przesyłane jest modulowane światło laserowe. Szybkośd z jaką
informacja może byd przekazywana przez falę (świetlną, radiową lub inną) jest
proporcjonalna do częstości. Aby zrozumied jakościowo
dlaczego
tak
się
dzieje,
rozważmy
modulowaną
(modyfikowaną) falę jako falę, w której niektóre grzbiety
zostają odcięte. Załóżmy, że każdy grzbiet reprezentuje cyfrę
binarną: odcięty grzbiet reprezentuje zero, a grzbiet
niezmodyfikowany – jeden. Ilośd cyfr binarnych, które mogą
byd wysłane w jednostce czasu jest zatem proporcjonalna do
częstotliwości fali. Światło w zakresie podczerwieni i w zakresie
widzialnym posiada częstotliwośd znacznie większą niż fale
radiowe. W rezultacie modulowany promieo laserowy może
przesyład ogromną ilośd informacji przez pojedyncze włókno
Rysunek 21.6
światłowodowe.
Inną zaletą włókien światłowodowych jest to, że są one znacznie cieosze od zwykłych
miedzianych przewodów, czyli więcej włókien może byd połączone w wiązkę o danej
średnicy. W związku z tym wyraźniejsze sygnały (na przykład różne linie telefoniczne) mogą
byd przesyłane za pomocą jednego kabla. Ponieważ włókna
2
światłowodowe są izolatorami, to są odporne na wszelkiego
𝒗
rodzaju zakłócenia elektryczne. Z tych powodów włókna optyczne
odgrywają
coraz
większą
rolę
w
przesyłaniu
obrazów
ds
telewizyjnych, telefonii, czy Internecie.
21.2 Zasada Fermata.
Jako podstawową zasadę optyki geometrycznej można przyjąd
zasadę podaną przez francuskiego matematyka Fermata. Z zasady
1
Rysunek 21.7
tej wynika prawo prostoliniowego rozchodzenia się promieni świetlnych oraz prawo
załamania i odbicia. W sformułowaniu Fermata zasada ta głosi:
Światło rozchodzi się po takiej drodze, której przebycie wymaga najkrótszego czasu.
Piotr Posmykiewicz – Wykład z fizyki
6
Na przejście odcinka ds (Rysunek 21.7) światło potrzebuje czasu dt = ds./v, gdzie v –
prędkośd światła w danym punkcie ośrodka. Zamieniając v na c/n, otrzymujemy dt =
(1/c)nds. A zatem czas τ potrzebny na przejście przez światło drogi od punktu 1 do 2 jest
równy:
𝛕=
𝟐
𝐧𝐝𝐬.
𝐜 𝟏
21.7
𝟐
𝐧𝐝𝐬
𝟏
21.8
𝟏
Wielkośd
𝑳=
nazywa się drogą optyczną. W ośrodku optycznie jednorodnym droga optyczna jest równa
iloczynowi drogi geometrycznej i współczynnika załamania ośrodka n:
𝐋 = 𝐧𝐬
21.9
Z 21.7 i 21.8 wynika, że
𝛕=
𝐋
𝐜
Proporcjonalnośd czasu τ od drogi optycznej umożliwia sformułowanie zasady Fermata w
następujący sposób:
Światło rozchodzi się po takich liniach, którym odpowiadają minimalne drogi optyczne.
Z zasady Fermata wynika odwracalność biegu promieni
A
świetlnych. Oczywiście droga optyczna, która jest minimalna przy
Z
B
przejściu światła od punktu 1 do 2 musi byd również minimalna przy
przejściu światła w kierunku przeciwnym.
O
O’
M
A’
Rysunek 21.8
Piotr Posmykiewicz – Wykład z fizyki
7
Wyprowadźmy prawo odbicia i załamania światła z zasady Fermata. Niech światło
wychodzące z punktu A, odbijając się od powierzchni
A
MN, trafia do punktu B (Rysunek 21.8). (Bezpośrednia
droga od A do B jest niemożliwa ze względu na
s1
a1
θ1
przegrodę Z). Ośrodek, w którym biegnie promieo, jest
ośrodkiem jednorodnym. Z tego względu minimum
drogi
optycznej
geometrycznej.
odpowiada
Długośd
minimum
drogi
dowolnej
drogi
geometrycznej jest równa AO’B = A’O’B (pomocniczy
punkt A’ jest odbiciem zwierciadlanym punktu A). Z
rysunku widad, że najmniejszą długośd ma droga
x
b
θ2
a2
s2
B
Rysunek 21.9
promienia odbijającego się w punkcie O w sytuacji, w której kąt odbicia jest równy kątowi
padania.
W celu wyprowadzenia prawa załamania, znajdźmy punkt, w którym promieo,
rozchodząc się od A do B, powinien ulec załamaniu tak, aby droga optyczna była minimalna
(Rysunek 21.9). Droga optyczna dowolnego promienia jest równa
L n1s1 n 2s 2 n1 a12 x 2 n 2 a 22 b x
2
W celu znalezienia minimum (ekstremum) policzmy pochodną L po x i przyrównajmy ją
do zera:
dL
dx
n1 x
a x
2
1
2
n 2 b x
a b x
2
2
2
n1
x
bx
n2
0
s1
s2
Czynniki przy n1 i n2 są odpowiednio równe sinθ1
i sinθ2. Tak więc:
n1sinθ1 n 2sinθ2
jest zależnością wyrażającą prawo załamania (patrz wzór 21.4).
Gorąca
powierzchnia
Rysunek 21.10
Piotr Posmykiewicz – Wykład z fizyki
8
Miraże są ciekawym przykładem zastosowania zasady Fermata. Na rozgrzanej słoocem
pustyni (może to byd asfalt szosy w upalny dzieo) powietrze przy samej powierzchni jest
najbardziej gorące. Im wyższa temperatura powietrza tym mniejsza jego gęstośd tym
mniejszy współczynnik załamania światła. Zatem najkrótszą drogą optyczną między
wielbłądem a człowiekiem nie będzie linia prosta a linia pokazana na rysunku 21.10.
Ponieważ oko rejestruje tylko kierunek, z którego dociera promieo świetlny, dlatego obraz
wielbłąda zobaczymy poniżej obrazu rzeczywistego. Równie dobrze można zjawisko to
wytłumaczyd w oparciu o zasadę Huygensa, o której jest mowa w następnym wykładzie.
21.3 Załamanie na powierzchni kulistej.
Dział optyki, w którym prawa rozchodzenia się światła rozpatruje się na podstawie
pojęcia promieni świetlnych nazywa się optyką geometryczną. Pod pojęciem promieni
świetlnych rozumie się normalne do powierzchni falowej linie, wzdłuż których
rozprzestrzenia się strumieo energii świetlnej. Optyka geometryczna pomimo iż jest metodą
przybliżoną, umożliwia, w sposób prosty, konstrukcję obrazów powstających w różnych
układach optycznych.
Jednym z najprostszych elementów dowolnego układu optycznego jest powierzchnia
sferyczna rozdzielająca dwa jednorodne optyczne ośrodki. Aby otrzymane wyniki były
prawdziwe zarówno dla wypukłych, jak i wklęsłych powierzchni wszystkim odcinkom i kątom
przypisuje się odpowiednie znaki w zależności od ich kierunków.
Na rysunku 21.11 rozpatrywane jest załamanie światła na powierzchni kulistej o
promieniu R, która rozdziela dwa ośrodki o współczynnikach załamania n a i nb. Punkt P jest
źródłem światła (przedmiotem). Prosta PP’ przechodząca przez punktowe źródło światła S i
Środek
krzywizny
C
powierzchni
sferycznej nazywa się osią optyczną
powierzchni
sferycznej.
Punkt
V
przecięcia powierzchni z osią optyczną
D
nazywa się wierzchołkiem powierzchni.
Promieo
SV
jest
prostopadły
do
powierzchni i przechodzi dalej nie
załamując się. Aby otrzymad obraz S’
–
Rysunek 21.11
Piotr Posmykiewicz – Wykład z fizyki
9
poprowadźmy dowolny promieo PB, który w punkcie B załamuje się i rozchodzi się wzdłuż
kierunku BP’.
Rozpatrzmy tylko promienie przyosiowe, tzn. tworzące z osią optyczną małe kąty
(odległośd h jest mała w porównaniu z R). Tylko dla promieni przyosiowych otrzymuje się
obraz stygmatyczny, tzn. wszystkie promienie wiązki przyosiowej, wychodzące z punktu P,
przecinają oś optyczną w jednym punkcie P’. Kierunki odcinków będziemy mierzyd od szczytu
powierzchni; jeżeli pokrywają się z promieniem będziemy przyjmowad je jako dodatnie, jeżeli
są po przeciwnej stronie promienia będziemy przyjmowad je jako ujemne. Dla promieni
przyosiowych pokazanych na rysunku 21.11 wszystkie kąty są małe, dlatego sinusy i
tangensy tych kątów można traktowad jako równe samym kątom.
Zgodnie z prawem załamania 𝑛𝑎 𝑠𝑖𝑛 𝜃𝑎 = 𝑛𝑏 𝑠𝑖𝑛 𝜃𝑏 . Zamieniając sinusy na kąty
otrzymujemy
𝑛𝑎 𝜃𝑎 = 𝑛𝑏 𝜃𝑏
21.10
Kąty (θa) i ϕ będąc kątami zewnętrznymi w stosunku do trójkątów PBC i P’BC są równe
sumie dwóch kątów wewnętrznych: 𝜃𝑎 = 𝜙 + 𝛼,
𝜙 = −𝜃𝑏 + 𝛽, czyli
𝜃𝑎 = 𝜙 + 𝛼
𝜃𝑏 = 𝜙 − 𝛽
21.11
Podstawiając do 21.11 otrzymamy:
𝑛𝑎 𝜙 + 𝛼 = 𝑛𝑏 𝜙 − 𝛽
Zamieniając małe kąty na ich funkcje trygonometryczne: 𝜙 ≈ 𝑅, 𝛼 ≈
𝑠
i 𝛽 ≈ 𝑠′
otrzymamy:
h h
h h
na nb ,
R s
R s'
skąd
nb
s′
+
na
s
=
n b −n a
R
21.12
W ten sposób, znając odległośd s od przedmiotu do powierzchni załamującej, można
wyliczyd odległośd s’ od powierzchni do obrazu. Przy wyprowadzaniu wzoru 21.12 wielkośd h
upraszcza się, co oznacza, że promienie przyosiowe, które wychodzą z punktu P, bez względu
jaki kąt tworzą one z osią optyczną, skupiają się w punkcie P’. We wzorze 21.12 promieo
krzywizny należy brad jako dodatni dla powierzchni wypukłej (środek krzywizny C leży na
prawo od wierzchołka V) lub ujemny dla powierzchni wklęsłej (C leży na lewo od O).
Piotr Posmykiewicz – Wykład z fizyki
10
Przez formalną zamianę na na (-nb) z równania na kulistą powierzchnię załamującą,
otrzymuje się równanie dla zwierciadła kulistego:
𝟏
𝟏
𝟐
+𝐬=𝐑=
𝐬′
𝟏
21.13
𝐟
Równanie zwierciadła kulistego.
gdzie f = R/2 nazywa się ogniskową zwierciadła kulistego. Jeżeli 𝑠 = ∞, wtedy 𝑠 ′ = 𝑓
tzn. promienie równoległe skupiają się w ognisku w odległości f od zwierciadła. Jeżeli źródło
umieścid w ognisku (s = f), to 𝑠′ = ∞, tzn., po odbiciu od zwierciadła kulistego wiązka światła
staje się równoległa. Jeżeli 𝑅 = ∞, (zwierciadło płaskie), to b = -a, tzn., obraz będzie
pozorny, „umiejscawiając się” symetrycznie za zwierciadłem. Rysunki 21.12a i b pokazują
a. Zwierciadło wklęsłe. R, s, s’ > 0
𝟏
𝟏
𝟐
+ =
𝐬′
𝐬
Rysunek 21.12
𝐑
b. Zwierciadło wypukłe. R < 0,
s > 0, s’ < 0
𝟏
𝟏
𝟐
+ =
𝐬′
𝐬
𝐑
przykładowe konstrukcje obrazów w przypadku zwierciadła wklęsłego i wypukłego.
Wródmy do sferycznej powierzchni załamującej i określmy zasady dotyczące znaków:
jeżeli środek krzywizny leży po stronie promieni wychodzących, to R jest dodatnie i jeżeli s’
leży po stronie promieni wychodzących, to jest dodatnie; czyli równanie 21.12 możemy
przepisad w postaci:
𝐧𝐚
𝐬
+
𝐧𝐛
𝐬′
=
𝐧𝐛 −𝐧𝐚
21.14
𝐑
Związek między przedmiotem a obrazem dla załamującej powierzchni sferycznej.
Równanie to nie zawiera kąta α, zatem
położenie obrazu jest takie samo dla
wszystkich
kątów
przyosiowych
wysyłanych z punktu P, co dowodzi
Rysunek 21.13
Piotr Posmykiewicz – Wykład z fizyki
11
prawdziwości naszego założenia, iż P’ jest obrazem P.
Aby otrzymad powiększenie liniowe m obrazu, wykorzystajmy konstrukcję
przedstawioną na rysunku 21.13. Z trójkątów PQV i P’Q’V:
tgθa =
y
tgθb =
s
−y′
s′
Prawo załamania:
na sinθa = nb sinθb
Dla małych kątów:
tgθa = sinθa i tgθb = sinθb
W rezultacie:
na y
s
=−
n b y′
s′
lub
𝐦=
𝐲′
𝐲
𝐧 𝐬′
= − 𝐧𝐚 𝐬
21.15
𝐛
Powiększenie liniowe, załamująca powierzchnia sferyczna.
Załamanie na zakrzywionej powierzchni jest jednym z powodów, dla którego
ogrodnicy starają się unikad podlewania roślin w środku dnia. Kiedy promienie słooca padają
na kroplę liścia, to ulegają załamaniu dążąc do skupienia się tak jak na rysunkach 21.12 i
21.13. Powoduje to skoncentrowanie energii i może uszkodzid roślinę.
Ważnym szczególnym przypadkiem ugięcia na powierzchni sferycznej jest przypadek, gdy
mamy płaską powierzchnię między dwoma ośrodkami. Wtedy R = ∞ i:
na
s
+
nb
s′
=0
21.16
Powiększenie w tym wypadku znajdziemy podstawiając to równanie do 21.15:
m=1
Jeżeli powierzchnia rozdziału ośrodków jest płaska, to zawsze
otrzymamy obraz tej samej wielkości co przedmiot.
21.4 Soczewki cienkie.
Jeżeli soczewki są na tyle cienkie, że analizując obrazy uzyskane
za ich pomocą możemy pominąd ich grubośd wtedy określamy je
mianem cienkich.
Soczewki pokazane na rysunku 21.14a mają tę własnośd, że jeżeli
wiązka promieni równoległych do osi optycznej przechodzi przez nie,
Rysunek 21.14
Piotr Posmykiewicz – Wykład z fizyki
12
to ulega skupieniu w punkcie F2. Takie soczewki nazywamy skupiającymi. Podobnie jeżeli
światło jest emitowane z punktu F1, to po przejściu przez soczewkę tworzy wiązkę
równoległą (Rysunek 21.14b). Punkty nazywają się pierwszym i drugim ogniskiem soczewki,
a odległośd od ogniska do środka soczewki nazywa się ogniskową. Pozioma linia łącząca
ogniska na rysunku 21.14a i b nazywa
się osią optyczną.
Rysunek 21.15 przedstawia jak
znaleźd
obraz
utworzony
przez
soczewkę i jakie jest jego powiększenie.
Dwa kąty zaznaczone jako α są
jednakowe,
czyli
dwa
trójkąty
Rysunek 21.15
prostokątne PQO i P’Q’O’ są podobne.
W związku z tym możemy zapisad:
y
s
y′
= − s′
lub
y′
y
s′
=−s
21.17
Również dwa kąty β są równe i trójkąty OAF2 i P’Q’F2 są podobne, zatem:
y
f
y′
= − s ′ −f lub
y′
y
=−
s ′ −f
f
21.18
Przekształcając 21.17 i 21.18 otrzymujemy ostatecznie:
𝟏
𝟏
+ 𝐬′ =
𝐬
𝟏
21.19
𝐟
Równanie przedmiot – obraz soczewki cienkiej.
Z powyższej analizy otrzymujemy również, że powiększenie liniowe m = y’/y z 21.17 jest
równe:
𝒎=
𝐲′
𝐲
=−
𝐬′
𝐬
21.20
Ujemny znak mówi nam, że kiedy s i s’ są dodatnie jak na
rysunku 21.15 wtedy obraz jest odwrócony, a y i y’ mają przeciwne
znaki.
Równania 21.19 i 21.20 są podstawowymi równaniami dla
soczewek cienkich. Obowiązują te same reguły dotyczące znaków.
W szczególności dla soczewki skupiającej (f dodatnie) kiedy
przedmiot znajduje się dalej od soczewki niż ogniskowa, wtedy
odległośd obrazu s’ jest dodatnia (obraz znajduje się po tej samej
stronie co wychodzący promieo), obraz jest rzeczywisty i
Rysunek 21.16
Piotr Posmykiewicz – Wykład z fizyki
13
odwrócony (rysunek 21.15). Jeżeli przedmiot umieszczony jest między ogniskiem, a
soczewką, wtedy s < f i s’ jest ujemne, co świadczy, że obraz jest po tej samej stronie co
przedmiot i jest urojony, prosty i powiększony.
Rysunek 21.16 przedstawia soczewki rozpraszające. Wiązka światła równoległego
padająca na taką soczewkę ulega rozproszeniu. Ogniskowa soczewek rozpraszających jest
ujemna – ogniska soczewek rozpraszających są zamienione miejscami w porównaniu z
soczewkami skupiającymi. Drugie ognisko soczewki rozpraszającej leży w punkcie przecięcia
przedłużeo promieni (Rysunek 21.16a), które padając równolegle do osi optycznej uległy
rozproszeniu (punkt, z którego wydają się wychodzid promienie).
Padające promienie, których przedłużenia zbiegają się w ognisku F1
(Rysunek 21.16b) wychodzą z soczewki rozpraszającej jako równoległe.
Równania 21.19 i 21.20 są prawdziwe zarówno dla soczewek
rozpraszających jak i skupiających. Soczewki różnego typu rozpraszające i
skupiające przedstawione są na rysunku 21.17. Zwródmy uwagę na
ważną obserwację: Każda soczewka, która jest grubsza w środku niż na
kraocach jest soczewką skupiającą i ma f > 0 i każda soczewka, która jest
grubsza na kraocach niż w środku jest soczewką rozpraszającą i posiada f
< 0.
Rysunek 21.17
Wielkośd:
𝐙=
𝟏
𝐟
nazywa się zdolnością zbierającą soczewki. Jednostką Z jest dioptria 1D = 1/m. Dla
soczewek skupiających Z jest większe od zera, a dla soczewek rozpraszających Z jest ujemne.
Jeżeli na przykład zdolnośd zbierająca wynosi -2D, to oznacza to, że ogniskowa jest równa
-50cm i soczewka jest soczewką rozpraszającą.
21.5 Równanie soczewki.
Piotr Posmykiewicz – Wykład z fizyki
14
Rozważmy ogólny przypadek kiedy mamy dwie powierzchnie kuliste oddzielające trzy
ośrodki o współczynnikach załamania na, nb, nc jak pokazane jest na rysunku 21.18.
Odległości przedmiotu i obrazu w przypadku pierwszej powierzchni wynoszą s1 i s1′ , a w
przypadku drugiej powierzchni s2 i s2′ . Zakładamy, że soczewka jest na tyle cienka (grubośd
Rysunek 21.18
t), że odległośd między tymi powierzchniami jest na tyle mała w porównaniu z odległością
przedmiotu i obrazu, że może byd zaniedbana. Wtedy s2 i s1′ mają tę samą wielkośd, ale
przeciwne znaki. Na przykład, jeżeli pierwszy obraz powstaje po stronie promieni
wychodzących z pierwszej powierzchni, wtedy s1′ jest dodatnie. Jeżeli jednak obserwowad
przedmiot od strony drugiej powierzchni, wtedy przedmiot nie znajduje się po stronie
promieni wchodzących do soczewki. W związku z tym s2 = −s1′ .
Musimy zastosowad dwa razy równanie 21.14 dla pojedynczej powierzchni: raz dla jednej
powierzchni, a raz dla drugiej powierzchni:
𝐧𝐚
𝐬𝟏
𝐧𝐛
𝐬𝟐
+ 𝐬′𝐛 =
𝐧
𝐧𝐛 −𝐧𝐚
𝐧𝐜
𝐧𝐜 −𝐧𝐛
𝐑𝟏
𝟏
+
𝐬𝟐′
=
𝐑𝟐
Zwykle pierwszym i trzecim ośrodkiem jest powietrze, czyli możemy zapisad n a = nc = 1.
Drugim ośrodkiem jest materiał soczewki, którego współczynnik załamania oznaczmy przez
n. Uwzględniając s2 = −s1′ otrzymujemy:
𝟏
𝐬𝟏
𝐧
𝐧−𝟏
𝟏
𝐑𝟏
+ 𝐬′ =
𝐧
𝟏
𝟏−𝐧
𝟏
𝟐
𝐑𝟐
− 𝐬′ + 𝐬′ =
Po przekształceniu otrzymujemy:
𝟏
𝐬𝟏
𝟏
𝟏
𝟐
𝐑𝟏
+ 𝐬′ = 𝐧 − 𝟏
𝟏
−𝐑
𝟐
Piotr Posmykiewicz – Wykład z fizyki
Zamieniając
s1
na
s
𝟏
𝐬
i
15
odległośd
𝟏
+ 𝐬′ = 𝐧 − 𝟏
koocowego
𝟏
obrazu
s2′
na
𝟏
𝐑𝟏
−𝐑
s’
otrzymujemy:
21.21
𝟐
Porównując 21.21 z 21.19 widzimy, że:
𝟏
𝐟
= 𝐧−𝟏
𝟏
𝐑𝟏
𝟏
−𝐑
21.22
𝟐
Równanie soczewki cienkiej.
Zwródmy uwagę, że jeżeli ośrodkiem otaczającym soczewkę nie jest powietrze, to n
oznacza względny współczynnik załamania nsocz/otocz ośrodka soczewki względem
otaczającego ośrodka (np. wody).
Równanie 21.22 podaje związek między promieniami krzywizn R1 i R2 soczewki, a
ogniskową soczewki. Można
użyd ten związek aby pokazad,
że
wszystkie
rysunku
soczewki
21.17a
na
Promień krzywizny
drugiej powierzchni
Promień krzywizny
pierwszej powierzchni
są
C1
soczewkami skupiającymi z
dodatnim
f,
a
wszystkie
soczewki na rysunku 21.17b
są
soczewkami
Rysunek 21.19
rozpraszającymi z f ujemnym.
Podane wcześniej reguły dotyczące znaków stosują się nadal do równao 21.21 i 21.22. Na
przykład na rysunku 21.19 s, s’ i R1 są dodatnie, a R2 jest ujemne.
Należy podkreślid, że wprowadzone przybliżenia dla cienkich soczewek rzeczywiście są
tylko przybliżeniami! Promienie, które padają pod dużymi kątami w stosunku do osi
optycznej soczewki sferycznej nie skupią się w tym samym miejscu co promienie przyosiowe;
jest to przyczyną aberracji sferycznej. Dlatego też, w precyzyjnych urządzeniach optycznych
soczewką nadaje się bardziej skomplikowany kształt.
21.6 Metody graficzne tworzenia obrazów.
Położenie obrazu możemy określid poprzez wybór dwu, trzech charakterystycznych
promieni, które wychodzą z danego punktu przedmiotu. Przecięcie się tych promieni po
Piotr Posmykiewicz – Wykład z fizyki
16
przejściu przez soczewkę określa położenie obrazu. Jak widad na rysunku 21.20 można
wybrad trzy charakterystyczne promienie:
1. Promieo równoległy do osi optycznej, który po przejściu przez soczewkę przechodzi
1
Rysunek 21.20
przez ognisko F2, lub wydaje się wychodzid z ogniska F2 w przypadku soczewki
rozpraszającej.
2. Promieo przechodzący przez środek soczewki, który nie ulega odchyleniu od kierunku
pierwotnego.
3. Promieo przechodzący przez ognisko F1 (lub, którego przedłużenie przechodzi przez
f.
Przedmiot O na zewnątrz ogniska.
Obraz I rzeczywisty.
e. Przedmiot O na zewnątrz ogniska, bliżej.
Obraz I rzeczywisty, dalej.
d. Przedmiot O na zewnątrz ogniska, jeszcze bliżej.
Obraz rzeczywisty I jeszcze dalej.
c. Przedmiot O w ognisku.
Obraz I w nieskończoności.
b. Przedmiot O wewnątrz ogniskowej.
Obraz pozorny.
a. Pozorny O przedmiot.
(promienie skupiają się na soczewce).
Rysunek 21.21
to ognisko w przypadku soczewki rozpraszającej) i który za soczewką biegnie
równolegle do osi optycznej.
Piotr Posmykiewicz – Wykład z fizyki
17
Rysunek 21.21 przedstawia szereg przypadków powstawania obrazów w przypadku soczewki
skupiającej. Należy samemu przeanalizowad poszczególne rysunki. Rysunek 21.21f
odpowiada pozornemu przedmiotowi. Padające promienie nie rozbiegają się z realnego
przedmiotu, ale zbiegają się jak gdyby wychodziły z czubka O pozornego przedmiotu po
prawej stronie. W tym wypadku s jest ujemne. W tym wypadku obraz jest rzeczywisty i leży
między soczewką a drugim ogniskiem. Sytuacja taka ma miejsce, jeżeli
padające na
soczewkę z rysunku 21.21f są skupiane po przejściu przez inną soczewkę skupiającą
niewidoczną na rysunku.
21.7 Powiększenie.
Określony rozmiar przedmiotu określony jest przez rozmiar jego obrazu na siatkówce.
Jeżeli oko jest nieuzbrojone, wtedy rozmiar ten zależy od kąta θ leżącego naprzeciwko
przedmiotu zwanego rozmiarem kątowym (Rysunek 21.22a).
Aby przyjrzed się dokładniej jakiemuś małemu przedmiotowi, przysuwamy go bliżej do
oka, a tym samym zwiększamy na ile to jest możliwe kąt przeciwległy do przedmiotu i obraz
na siatkówce. Jednak nasze oko nie jest w stanie zogniskowad się na przedmiocie, który jest
bliżej niż odległośd dobrego widzenia, w związku z czym rozmiar kątowy przedmiotu osiąga
swoją największą możliwą wartośd kiedy znajduje się w odległości dobrego widzenia. W
dalszych rozważaniach będziemy przyjmowad, że średnia odległośd dobrego widzenia wynosi
25cm.
Soczewki skupiające można użyd do stworzenia obrazu pozornego, który będzie większy i
dalej położony od oka niż sam przedmiot, tak jak to jest pokazane na rysunku 21.22b.
Soczewkę użytą w ten sposób nazywamy lupą (szkło powiększające). Obraz pozorny
najwygodniej ogląda się, jeżeli położony jest w nieskooczoności, wtedy mięsieo rzęskowy
źrenicy jest najbardziej rozluźniony i w dalszej dyskusji będziemy zakładad, że tak właśnie
jest.
Na rysunku 21.22a przedmiot znajduje się w pobliżu punktu, dla którego rozmiar kątowy
wynosi θ. Na rysunku 21.22b szkło powiększające przed okiem wytwarza obraz w
nieskooczoności, a rozmiar kątowy jest równy θ’. Skutecznośd działania lupy określona jest
poprzez stosunek kąta θ’ (z lupą) do kąta θ (bez lupy). Iloraz ten nazywa się powiększeniem
kątowym:
Piotr Posmykiewicz – Wykład z fizyki
𝐌=
18
𝛉′
21.23
𝛉
Powiększenie kątowe.
Uwaga. Nie należy mylid powiększenia liniowego z powiększeniem kątowym. Powiększenie
kątowe jest stosunkiem rozmiarów kątowych, podczas gdy powiększenie liniowe jest
stosunkiem rozmiarów liniowych. Na rysunku 21.22b powiększenie kątowe wynosi około 3X,
ponieważ mrówka widoczna jest pod kątem trzy razy większym niż na rysunku 21.22a.
Powiększenie liniowe wynosi m = -s’/s na rysunku 21.22b i jest równe nieskooczenie duże,
ponieważ obraz pozorny znajduje się w nieskooczoności, nie oznacza to jednak, że mrówka
jest nieskooczenie duża, kiedy patrzymy przez lupę!
Aby znaleźd wartośd M przyjmijmy, że kąty są na tyle małe, iż każdy kąt w radianach
może byd przybliżony jego sinusem i tangensem. Korzystając z rysunku 21.22a i rysując
promieo, który na rysunku 21.22b przechodzi nieodchylony przez środek soczewki możemy
obliczyd kąty θ’ i θ:
𝑦
𝑦
𝜃′ = 𝑓
𝜃 = 25𝑐𝑚
Podstawiając te wyrażenia do 21.23 otrzymujemy
𝐌=
𝛉′
𝛉
𝐲/𝐟
= 𝐲/𝟐𝟓𝐜𝐦 =
𝟐𝟓𝐜𝐦
21.23
𝐟
Powiększenie kątowe lupy.
Mogło by się wydawad, że możemy
zwiększyd powiększenie kątowe do
dowolnej
wielkości
poprzez
Okular
zmniejszenie ogniskowej f. Jednak z
powodu
aberracji
dwuwypukłej
soczewki
zwykłej
Obraz
rzeczywisty
granica
powiększeo wynosi od 3X do 4X. Do
uzyskania
większych
powiększeo
Obiektyw
stosujemy mikroskop.
Okular
Przedmiot
21.8 Mikroskop.
Podstawowe składniki mikroskopu
Źródło
światła
przedstawione są na rysunku 21.23a.
Obiektyw
Oglądany przedmiot O umieszcza się
Rysunek 21.23
Piotr Posmykiewicz – Wykład z fizyki
19
zaraz za pierwszym ogniskiem F1 obiektywu, który daje powiększony i rzeczywisty obraz
przedmiotu I (Rysunek 21.23b). Obraz ten leży zaraz za pierwszym ogniskiem F1′ okularu.
Okular działa jak zwykła lupa i tworzy końcowy pozorny obraz I’ przedmiotu I. Położenie
obrazu I’ może być w dowolnym miejscu w punktach zarówno blisko lub i daleko od oka. W
rzeczywistych mikroskopach w celu uzyskania dobrej jakości obrazu zarówno okular, jak i
obiektyw składają się z wielu elementów optycznych, które dla prostoty objaśnień możemy
pominąć.
Tak samo jak w przypadku lupy o wielkości powiększenia w mikroskopie decyduje
powiększenie kątowe M. Całkowite powiększenie kątowe mikroskopu jest iloczynem dwu
czynników. Pierwszy składnik to powiększenie liniowe m1 obiektywu, które określa rozmiary
obrazu rzeczywistego I; drugi czynnik jest powiększeniem kątowym M2 okularu, które
związane jest z rozmiarem kątowym obrazu pozornego widzianym przez okular w
porównaniu z rozmiarem kątowym obrazu rzeczywistego, który byłby obserwowany bez
użycia okularu. Pierwszy z tych czynników dany jest przez:
𝑠′
𝑚1 = − 𝑠1
1
gdzie s1 i s1′ są odległościami od przedmiotu i obrazu od soczewki obiektywu. Zwykle
przedmiot znajduje się bardzo blisko ogniskowej i dlatego odległośd obrazu 𝑠1′ jest bardzo
duża w porównaniu z ogniskową f1 obiektywu. Zatem
s1 ≈ f1 i możemy zapisad, że
m1 = −s1′ /f1 .
Obraz rzeczywisty I znajduje się blisko ogniska F1′ okularu, dlatego aby znaleźd
powiększenie kątowe możemy zastosowad wzór 21.23: M2 = 25cm /f2 , gdzie f2 jest
ogniskową okularu. Całkowite powiększenie kątowe M mikroskopu (z pominięciem znaku
minus) jest iloczynem tych dwu powiększeo:
𝐌 = 𝐦𝟏 𝐌𝟐 =
𝟐𝟓𝐜𝐦 𝐬𝟏′
𝐟𝟏 𝐟𝟐
21.24
Powiększenie kątowe mikroskopu.
gdzie s1′ f1 i f2 mierzone są w centymetrach. Koocowy obraz jest odwrócony w porównaniu
do przedmiotu. Producenci mikroskopów zwykle podają wartości m1 i M2.
21.9 Teleskop.
Piotr Posmykiewicz – Wykład z fizyki
20
Układ optyczny stosowany w teleskopach przypomina ten z którego, składa się
mikroskop. W obu urządzeniach obraz jest tworzony za pomocą obiektywu i obserwuje się
go przez okular. Kluczową różnicą jest to, że teleskop jest używany do obserwowania dużych
Obiektyw
Okular
Obiektyw
Okular
I’ w ∞
Rysunek 21.24
obiektów znajdujących w dużej odległości od obserwatora. Inną różnicą jest to, iż w
teleskopach często stosuje się zwierciadła wklęsłe w miejsce obiektywu.
Teleskop astronomiczny (luneta Keplera) pokazany jest na rysunku 21.24. Soczewki
obiektywu tworzą obraz I rzeczywisty i pomniejszony obiektu. Ten obraz jest przedmiotem
dla soczewek okularu, który daje powiększony obraz pozorny. Obiekty obserwowane przez
lunetę znajdują się zwykle tak daleko od obserwatora, że obraz I powstaje bardzo blisko
drugiej ogniskowej obiektywu. Jeżeli koocowy obraz I’ utworzony przez okular znajduje się w
nieskooczoności (dla najbardziej komfortowego patrzenia), wtedy pierwszy obraz musi
znajdowad się w tuż przy pierwszym ognisku okularu. W rezultacie odległośd między
obiektywem, a okularem jest równa sumie ogniskowych f1 + f2.
Powiększenie kątowe M teleskopu zdefiniowane jest jako stosunek rozmiaru kątowego
koocowego obrazu I’ do kąta obserwacji obiektu okiem nieuzbrojonym. Na rysunku 21.24 kąt
θ jaki tworzy promieo padający na obiektyw pochodzący od obiektu (niepokazanego na
rysunku) z osią optyczną jest jednocześnie kątem pod jakim widoczny jest ten obiekt okiem
nieuzbrojonym. Jednocześnie, ponieważ oko obserwatora znajduje się bezpośrednio na
prawo za ogniskiem F2′ , to kąt, pod którym widziany jest obraz koocowy jest praktycznie
równy kątowi θ’. Ponieważ bd jest równoległe do osi optycznej, to odcinki ab i cd są sobie
równe jak również są równe wysokości y’ obrazu rzeczywistego I. Ponieważ θ i θ’ są małe, to
Piotr Posmykiewicz – Wykład z fizyki
21
można je wyrazid za pomocą tangensów. Z trójkątów prostokątnych F 1ab i F2′ cd
otrzymujemy:
𝑦′
𝜃 = −𝑓
1
𝑦′
𝜃′ = − 𝑓
2
W rezultacie powiększenie kątowe M:
𝐌=
𝛉′
𝛉
𝐟
= − 𝐟𝟏
21.25
𝟐
Powiększenie kątowe teleskopu.
Znak minus wskazuje, że obraz jest odwrócony. Równanie 21.25 pokazuje, że jeżeli chce się
uzyskad duże powiększenie kątowe, to powinno się stosowad obiektywy o dużej ogniskowej
f1. Sytuacja jest odwrotna niż w mikroskopie, gdzie otrzymamy tym większe powiększenie im
krótsza będzie ogniskowa obiektywu. Jednak obiektyw teleskopu o dużej ogniskowej
powinien posiadad również dużą średnicę D, tak aby wartośd przesłony nie była zbyt duża
(duża wartośd przesłony f1/D oznacza, że obraz jest zamglony i posiada małe natężenie). W
typowych teleskopach obiektywy nie są wymienialne, zmienia się natomiast okulary; tak jak
w mikroskopie im mniejsza ogniskowa f2 okularu tym większe powiększenie kątowe
teleskopu.
Odwrócenie obrazu nie jest jedyną wadą teleskopu. Kiedy używamy teleskopu albo
lornetki – w istocie dwu lunet zamocowanych obok siebie, chcielibyśmy, aby obraz
obserwowanych przedmiotów był prosty. W lornetkach osiąga się to poprzez kilkakrotne
odbicie promieni świetlnych od pryzmatów umieszczonych wewnątrz między obiektywem a
okularem. Na lornetkach podaje się zwykle opis w postaci np.
7 X 50. Pierwsza liczba określa powiększenie kątowe M, a
Obudowa wraz
z drugim
zwierciadłem
druga jest średnicą obiektywu (w milimetrach). Średnica
obiektywu pozwala określid zdolnośd soczewek obiektywu do
skupiania światła, a tym samym determinuje jasnośd obrazu.
W teleskopach odbiciowych (Rysunek 21.25) soczewki
obiektywu zastąpione są przez zwierciadło wklęsłe. W dużych
teleskopach
ten
sposób
ma
wiele
zalet,
zarówno
Obiektyw
teoretycznych jak i praktycznych. Zwierciadła z swojej istoty
Otwór w
zwierciadle
obiektywu
są wolne od aberracji chromatycznej, a aberracja sferyczna
jest łatwiejsza do korygowania. Czasami kształt zwierciadeł
jest paraboliczny, a nie sferyczny. Materiał zwierciadeł nie
Rysunek 21.25
Piotr Posmykiewicz – Wykład z fizyki
22
musi byd przezroczysty i może byd wykonany nie tak dokładnie jak materiał używany do
soczewek (soczewki mogą oczywiście byd osadzane tylko przy swoich krawędziach). Tym
niemniej powierzchnia zwierciadeł obiektywu, na przykład teleskopu należącego do The
European Southern Observatory w północnym Chile, jest polerowana z dokładnością do
8,5 ∙ 10−9 m, co odpowiada średnicy około tuzina atomów.
Największe na świecie teleskopy odbiciowe – teleskopy Kecka umieszczone na szczycie
Mauna Kea na Hawajach posiadają zwierciadła o średnicy 10m składające się z 36
oddzielnych sześciokątnych elementów. Soczewki, które mają średnicę większą niż 1m nie
mają już praktycznego zastosowania.
Jednym z wyzwao przy projektowaniu teleskopów jest to, iż obraz powstaje naprzeciwko
zwierciadła obiektywu, w obszarze padających promieni światła. Rysunek 21.24 przedstawia
jeden ze sposobów rozwiązania tego problemu; promienie świetlne odbite od zwierciadła
obiektywu są przechwytywane przez drugie zwierciadło, które odbija światło w kierunku
otworu w obiektywie. Obraz koocowy jest obserwowany w pewnej odległości po drugiej
stronie zwierciadła obiektywu.
Jeżeli mają byd robione zdjęcia przy pomocy teleskopu, to w miejscu powstawania obrazu
rzeczywistego tworzonego przez obiektyw umieszcza się film lub detektor elektroniczny. W
większości teleskopów używanych w badaniach astronomicznych nigdy nie stosuje się
okularów.
21.10 Aparat fotograficzny.
Jednymi
z
najbardziej
rozpowszechnionych
urządzeo
optycznych
są
aparaty
fotograficzne, które wytwarzają obraz rzeczywisty i zapisują go elektronicznie lub na filmie.
Podstawowymi częściami aparatu
są:
zamknięty
(soczewki
korpus,
skupiające),
obiektyw
migawka
Obraz
rzeczywisty
Migawka
Obiektyw
Naświetlany
film
odsłaniająca soczewki na zadany czas i
medium rejestrujące obraz (matryca
światłoczuła lub film) (Rysunek 21.26).
Soczewki wytwarzają rzeczywisty obraz
fotografowanego obiektu. Wysokiej
klasy obiektyw składa się z szeregu
elementów,
które
umożliwiają
Obiekt
Przesłona
Rysunek 21.26
Piotr Posmykiewicz – Wykład z fizyki
23
korekcję różnego rodzaju aberracji (chromatycznej i sferycznej).
Jeżeli ustawiona jest właściwa ostrośd, wtedy następuje zgranie odległości obiektu z
obrazem utworzonym na matrycy światłoczułej. Otrzymana fotografia będzie wtedy
maksymalnie ostra. Jeżeli mamy soczewki skupiające, to wraz ze wzrastaniem odległości
obrazu maleje odległośd do obiektu (Rysunek 21.21a,b,c). Z tego powodu jeżeli aparat
250
(105mm)
Rysunek 21.27
ogniskuje się na dalekim przedmiocie obiektyw przybliża się do matrycy, a jeżeli
fotografujemy przedmiot z bliska obiektyw oddala się od matrycy światłoczułej.
Wybór ogniskowej f obiektywu aparatu fotograficznego zależy od rozmiaru filmu lub
matrycy, jak również od pożądanego kąta widzenia. Rysunek 21.27 przedstawia trzy
fotografie zarejestrowane na 35mm filmie wykonane tym samym aparatem ustawionym w
tym samym miejscu, jednak przy różnych długościach ogniskowej. Obiektyw o dużej
ogniskowej, zwany teleobiektywem, daje mały kąt widzenia i duży obraz odległego obiektu
(taki jak pomnik na rysunku 21.27c); obiektyw posiadający krótką ogniskową daje mały
obraz i szeroki kąt widzenia (taki jak na rysunku 21.27a) i nazywa się obiektywem
szerokokątnym. Aby zrozumied takie zachowanie przypomnijmy sobie, że ogniskowa jest
równa odległości od soczewki do obrazu, gdy przedmiot znajduje się w nieskooczoności.
Ogólnie, dla dowolnej odległości od obiektu, użycie obiektywu o dłuższej ogniskowej
powoduje powstanie obrazu dalej od obiektywu. powoduje to również wzrost wysokości
Piotr Posmykiewicz – Wykład z fizyki
24
obrazu; jak była mowa wcześniej, stosunek wysokości y’ obrazu do wysokości y obiektu
(powiększenie liniowe) jest równy wartości bezwzględnej ze stosunku odległości obrazu s’ do
odległości przedmiotu s (równanie 21.10):
𝒎=
𝐲′
𝐲
𝐬′
=−𝐬
Dla obiektywu o krótkiej ogniskowej stosunek s’/s jest mały i daleki obiekt tworzy mały
obraz. Kiedy używamy obiektywu o długiej ogniskowej, wtedy obraz tego samego obiektu
może całkowicie wypełnid kadr filmu. W rezultacie im dłuższa ogniskowa tym węższy kąt
widzenia (Rysunek 21.27d).
Aby obraz na filmie (matrycy) został utrwalony właściwie, całkowita energia na jednostkę
powierzchni musi byd zawarta w określonych granicach. Osiąga się to poprzez odpowiedni
dobór migawki i przesłony. Migawka określa przedział czasu, w którym światło wpada przez
1
obiektyw. Często czasy migawki zawierają się od 2s do 1000 s.
Natężenie światła wpadającego do obiektywu jest proporcjonalne do obszaru „widzianego”
przez obiektyw i do efektywnej powierzchni obiektywu. Wielkośd powierzchni, która jest
„widziana” przez obiektyw jest proporcjonalna do kwadratu kąta widzenia obiektywu, a
zatem z grubsza, jest proporcjonalna do 1/f2. Efektywna powierzchnia obiektywu jest
regulowana za pomocą zmiennej średnicy obiektywu D zwanej przesłoną. Zatem efektywna
powierzchnia jest proporcjonalna do D2. Łącząc te dwa czynniki razem widzimy, że natężenie
światła docierającego do matrycy światłoczułej przez określony obiektyw jest proporcjonalne
do D2/f2. Zdolnośd obiektywu do gromadzenia światła jest
powszechnie określana w fotografii za pomocą tzw. liczby
Skala
przesłonowej zdefiniowanej jako stosunek f/D:
𝑂𝑔𝑛𝑖𝑠𝑘𝑜𝑤𝑎
𝑙𝑖𝑐𝑧𝑏𝑎 𝑝𝑟𝑧𝑒𝑠ł𝑜𝑛𝑜𝑤𝑎 = Ś𝑟𝑒𝑑𝑛𝑖𝑐𝑎
𝑝𝑟𝑧𝑒𝑠 ł𝑜𝑛𝑦
𝑓
=𝐷
Na przykład jeżeli obiektyw posiada ogniskową f = 50mm i średnicę D
= 25mm, to mówimy, że posiada liczbę przesłonową 2, lub przesłonę
Zmienna
przesłona
Przesłona f/4
f/2. Natężenie światła docierającego do filmu (matrycy) jest
odwrotnie proporcjonalne do liczby przesłonowej.
W
obiektywach
zwiększymy średnicę
posiadających
zmienną
przesłonę,
2 razy, to liczba przesłonowa zmaleje
jeżeli
2
razy, a natężenie światła wpadającego przez obiektyw wzrośnie
Przesłona f/8
Rysunek 21.28
Piotr Posmykiewicz – Wykład z fizyki
25
dwukrotnie. Regulowane przesłony posiadają zwykle skale opisane liczbami będącymi
wielokrotnościami
f/2
2, taki jak:
f/2,8
f/4
f/5,6
f/8
f/11
f/16
itd. Największa liczba przedstawia najmniejszą średnicę i naświetlenie, a każda zmiana
przesłony o jeden krok powoduje zmianę natężenia światła o 2 (Rysunek 21.28). Całkowita
ekspozycja (całkowita ilośd światła padająca na matrycę czy film) jest proporcjonalna
1
1
zarówno do powierzchni otworu jak i czasu otwarcia migawki. Tak więc f/4 i 500 s, f/5,6 i 250 s
1
i f/8 i 125 s odpowiadają tej samej ekspozycji.
Podczas fotografowania często używa się obiektywu z „zoomem”. Taki obiektyw składa się
z układu soczewek, które pozwalają zmieniad ogniskową w sposób ciągły. W pojedynczych
przypadkach w aparatach kompaktowych ogniskowa zmienia się nawet osiemnastokrotnie.
Rysunek 21.29a i b
przedstawia
układ
Obraz
prosty
ze
zmienną
ogniskową;
długośd
ogniskowej
układu
Rysunek 21.29
zależy od wzajemnej odległości między soczewkami.
21.11 Aberracje układów optycznych.
Rozpatrując przechodzenie światła przez cienkie soczewki ograniczyliśmy się tylko do
promieni przyosiowych. Współczynnik załamania światła uważaliśmy za niezależny od
długości padającej fali świetlnej, a światło padające traktowaliśmy jako monochromatyczne.
Ponieważ w rzeczywistych układach optycznych warunki te często nie są spełnione, to
prowadzi to do zniekształceo obrazu zwanych aberracjami.
Piotr Posmykiewicz – Wykład z fizyki
1.
promienie
26
Aberracja sferyczna. Jeżeli na soczewkę pada rozbieżna wiązka światła, to
przyosiowe
po
δ
przejściu przez soczewkę przetną
S
się w punkcie S’, a promienie
S’’
bardziej oddalone od osi – w
S’
punkcie S’’, bliższym soczewki
(Rysunek 21.30). W rezultacie na
Rysunek 21.30
ekranie prostopadłym do osi
optycznej powstanie obraz świecącego punktu w postaci rozmytej plamki. Ten rodzaj
zniekształceo, związany ze sferycznością załamującej
powierzchni nazywa się aberracją sferyczną. Miarą
ilościową aberracji sferycznej jest odcinek δ = OS’’ – OS’.
W celu zmniejszenia aberracji sferycznej stosuje się
diafragmy (przesłony), jednak jednocześnie zmniejsza się
(a)
przy tym strumieo światła przechodzący przez soczewkę.
Aberrację sferyczną można praktycznie wyeliminowad
stosując układy składające się z soczewek rozpraszających
(δ > 0) i skupiających (δ < 0).
2. Koma. Jeżeli przez układ optyczny przechodzi
(b)
szeroka wiązka pochodząca od świecącego punktu
znajdującego się poza osią optyczną, to otrzymany obraz
tego punktu będzie miał kształt świecącej plamki,
wyglądem
przypominającej
ogon
komety.
Takie
zniekształcenie nazywa się komą. W celu pozbycia się
komy stosuje się takie same metody jak w przypadku
eliminacji aberracji sferycznej.
3. Dystorsja. Dystorsją nazywa się zniekształcenie
(c)
Rysunek 21.31
polegające na tym, że dla promieni padających pod dużymi kątami na soczewkę,
powiększenie liniowe punktów przedmiotu, które znajdują się w różnych odległościach od
głównej osi optycznej jest różne. W rezultacie ulega naruszeniua)geometryczne podobieostwo
przedmiotu (Rysunek 21.31a) i obrazu (Rysunek 21.31b,c).
Piotr Posmykiewicz – Wykład z fizyki
27
4. Aberracja chromatyczna. Do tej pory zakładaliśmy, ze współczynniki załamania
światła układu optycznego są jednakowe. Jest to jednak prawdziwe tylko dla układu
optycznego oświetlanego światłem monochromatycznym (λ = const.). Jeżeli światło ma
złożony charakter (różne wartości
b)
λ), to należy uwzględniad zależnośd
współczynnika
załamania
S
materiału soczewki (i otaczającego
ośrodka,
jeżeli
nie
jest
to
powietrze) od długości fali zjawisko
Rysunek 21.32
dyspersji). Jeżeli na układ optyczny pada światło białe, to poszczególne monochromatyczne
składowe będą ogniskowad się w różnych punktach (najdłuższą ogniskową mają promienie
czerwone, najmniejszą – promienie fioletowe) (Rysunek 21.32). W rezultacie na ekranie
otrzymamy rozmytą plamkę, zabarwioną na brzegach. Zjawisko to nosi nazwę aberracji
chromatycznej. Ponieważ różne rodzaje szkieł posiadają różną dyspersję, to tworząc
kombinację soczewek rozpraszających i skupiających wykonanych z różnych szkieł, można
pozbyd się aberracji chromatycznej.
5. Astygmatyzm. Zniekształcenie spowodowane niejednakową krzywizną powierzchni
optycznej dla różnych przekrojów poprzecznych soczewki padającej wiązki nazywa się
astygmatyzmem. Obraz punktu oddalonego od osi optycznej jest obserwowany na ekranie w
postaci rozmytej, eliptycznej plamki. Plamka ta, w zależności od odległości do środka
optycznego, ulga deformacji i zmienia się w pionowy lub poziomy odcinek. Astygmatyzm
można skompensowad wybierając soczewki o odpowiednich krzywiznach powierzchni
załamujących.
21.12 Wielkości i jednostki fotometryczne.
Fotometrią nazywa się dział optyki zajmujący się pomiarem strumieni świetlnych i wielkości z
nimi zawiązanych.
Źródło światła, którego rozmiary są zaniedbywalnie małe w porównaniu z odległością od
niego do miejsca detekcji, nazywa się źródłem punktowym. W ośrodku jednorodnym i
izotropowym fala emitowana przez źródło punktowe jest falą kulistą. Do scharakteryzowania
punktowych źródeł światła używa się pojęcia natężenie światła I, które definiuje się jako
strumieo promieniowania źródła, przypadający na jednostkowy kąt bryłowy:
Piotr Posmykiewicz – Wykład z fizyki
28
𝐝𝚽
𝐈=
21.26
𝐝𝛀
Natężenie światła I
(dΦ – strumieo świetlny emitowany przez źródło w kąt bryłowy dΩ).
W ogólności natężenie światła zależy od kierunku. Jeżeli I nie zależy od kierunku, to
źródło nazywa się źródłem izotropowym. W przypadku źródła izotropowego
Φ
𝐼 = 4π
21.27
gdzie Φ – całkowity strumieo świetlny emitowany przez źródło we wszystkich możliwych
kierunkach.
Jednostka natężenia światła – kandela (cd) jest jedną z podstawowych jednostek
międzynarodowego układu miar SI.
Kandela jest to natężenie światła, którą ma w określonym kierunku źródło emitujące
promieniowanie monochromatyczne o częstości 5,4 ∙ 1014 Hz i którego natężenie w tym
kierunku jest równe (1/683)W/sr.
Jednostką strumienia świetlnego jest lumen (lm).
Jest on równy strumieniowi świetlnemu, emitowanemu przez źródło o natężeniu 1cd w
kąt bryłowy 1 steradiana:
1lm = 1cd ∙ 1str
Stopieo oświetlenia jakiejś powierzchni przez padające na nią światło określa wielkośd:
𝐄=
𝐝𝚽𝐩𝐚𝐝
𝐝𝐒
,
6.19
nazywa się oświetleniem (dΦ – strumieo świetlny padający na element powierzchni dS.).
Jednostką oświetlenia jest lux (lx), który równy jest oświetleniu wywołanemu przez
strumieo 1lm równomiernie rozłożony na powierzchni 1m2:
1lux 1lm :1m2 .
Oświetlenie wywołane przez źródło punktowe można wyrazid przez natężenie
oświetlenia I, odległośd r powierzchni oświetlanej od źródła i kąt α między normalną do
powierzchni n i prostą w kierunku źródła. Na powierzchnię dS (Rysunek 21.33) pada
strumieo dΦ = IdΩ, przypadający na kąt bryłowy dΩ oparty na powierzchni ds. Kąt dΩ jest
równy dScosα/r2. Tak więc dΦ = I dScosα/r2. Dzieląc ten strumieo przez dS., otrzymujemy
Piotr Posmykiewicz – Wykład z fizyki
𝐄=
29
𝐈𝐜𝐨𝐬𝛂
𝐫𝟐
dΩ
𝒏
𝒓
α
dS
Rysunek 21.33