Dzielnik napięcia raz jeszcze

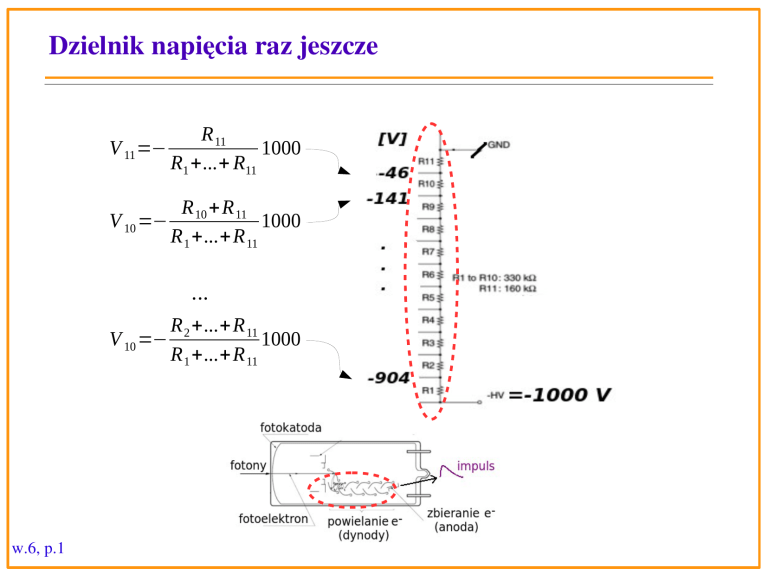
Dzielnik napięcia raz jeszcze
V 11 =−
R 11
1000
R1 +...+ R11
V 10 =−
R 10 +R 11
1000
R 1 +...+R 11
...
R 2 +...+R 11
V 10 =−
1000
R 1 +...+R 11
w.6, p.1 Detektor jąder superciężkich­demonstracja
cząstki naładowane
(np.: Cn)
zdarzenie (event)
Tarcza (Th)
jony wiązki
(Au)
w.6, p.2 dyskretny w czasie i wartościach
Metody liczenia układów liniowych ­ przypomnienie
Superpozycja sygnałów
Odpowiedź układu liniowego na kilka wymuszeń (źródeł) jest równa sumie algebraicznej odpowiedzi na każde wymuszenie oddzielnie.
Twierdzenie Thévenina (metody liczenia układów liniowych)
Każdy liniowy dwójnik aktywny można zastąpić równoważnym układem, zawierającym źródła napięcia vth połączone szeregowo z oporem RTh (impedancją).
Twierdzenie Nortona (metody liczenia układów liniowych)
Każdy liniowy dwójnik aktywny można zastąpić równoważnym układem,
zawierającym źródło prądu iN połączone równolegle z oporem RN (impedancją).
w.6, p.3 Filtry ­ przypomnienie
Układ różniczujący – Wymuszenie sinusoidalne
górno­przepustowy
w.6, p.4 Układ całkujący – Wymuszenie sinusoidalne
dolno­przepustowy
Filtry ­ przypomnienie
Układ różniczujący – impulsy o kształcie prostokąta
w.6, p.5 Układ całkujący – impulsy o kształcie prostokąta
Filtry ­ przypomnienie
Filtr Wiena w.6, p.6 Linia długa: czwórnik o elementach rozłożonych
Za pomocą linii długiej przesyłamy sygnały (impulsy) elektryczne od nadajnika do odbiornika.
Izolacja
Przewód sygnałowy
Odbiornik
Generator
Δx
x
Izolacja (teflon)
Oplotka, przewód masy
Linia jednorodna – parametry na jednostkę długości nie zależą od współrzędnej x
w.6, p.7 Linia długa: model linii bez strat
Na podstawie p. KVL:
∂ i( x ,t )
u( x , t)=L Δ x
+ u( x + Δ x ,t )
∂t
Na podstawie p. KCL:
i
LΔ x
u
∂ u( x , t)
i( x ,t )=C Δ x
+i (x + Δ x ,t )
∂t
przekształcając:
u(x + Δ x ,t )−u ( x ,t )
∂ i( x , t)
=−L
Δx
∂t
i( x+ Δ x , t)−i( x , t)
∂ u( x , t)
=−C
Δx
∂t
jeśli: Δ x →0
to:
i +Δ i
CΔx
u+ Δ u
x +Δ x
L, C odnoszą się do jednostki długości linii.
∂u ( x ,t )
∂i( x , t)
=−L
;
∂x
∂t
∂i (x , t)
∂ u(x , t)
=−C
∂x
∂t
u(x,t), i(x,t) – uogólnione napięcie i prąd (zespolone)
w.6, p.8 Linia długa: model linii bez strat
∂ ∂u (x , t) = −∂ L ∂i( x , t)
∂x ∂ x
∂x
∂t
∂ ∂i(x , t) = −∂ C ∂u (x , t)
∂t ∂ x
∂t
∂t
2
2
∂ u ( x , t)
∂ i( x , t )
=−L
2
∂x∂t
∂x
∂ 2 i(x , t)
∂ 2 u (x , t)
=−C
∂t ∂ x
∂t 2
2
Podobnie można otrzymać:
2
∂ u (x , t)
∂ u ( x ,t )
=−LC
2
2
∂x
∂t
2
2
(*)
∂ i( x , t)
∂ i( x , t)
=−LC
(**)
2
2
∂x
∂t
Są to równania fali rozchodzącej się z prędkością:
w.6, p.9 1
vf 
LC
­ vf prędkość fazowa.
Linia długa: model linii bez strat
Uwaga!
Rozwiązanie ogólne równań (*) i (**) ma postać dwóch fal rozchodzących się (fala biegnąca i fala odbita) w przeciwnych kierunkach:
u( x , t)=u← (x + v f t)+ u→( x−v f t)
i( x ,t )=i ← ( x+ v f t)+i →( x−v f t)
Definiujemy impedancję charakterystyczną linii długiej:
Z 0=
u← u→
=
i← i →
→ Z 0=
√
L
C
A taką ma postać fala biegnąca i odbita dla sygnału wejścia typu sinus:
u( x , t)=( A 1 e j ω √ LC + A 2 e− j ω √ LC ) e
i(x ,t )=
j ωt
1
jωt
( A 1 e j ω √ LC − A 2 e− j ω √ LC )e
Z0
w.6, p.10 fala biegnąca
fala odbita
Rzeczywista linia długa: model odcinka linii długiej
i
RΔ x
i +Δ i
R, L, C, G odnoszą się do jednostki długości linii.
LΔ x
u
CΔx
GΔx
u+ Δ u
x +Δ x
R G
­ linia zrównoważona
jeśli: =
L C
W tym szczególnym przypadku mamy:
Z 0=
√
R
L + jω
L
( )= L
C
√
G
C ( + j ω)
C
w.6, p.11 Impedancja charakterystyczna linii
rzeczywistej:
R+ j ω L
Z 0 (ω)=
G+ j ω C
√
Zachodzi:
Z 0 (ω) : zależy od częstości
v f (ω) : zależy od częstości
­ amplituda fali jest tłumiona
Jeśli R=G=0 to otrzymujemy linię długą bez strat.
Linia długa: kiedy?
w.6, p.12 Współczynnik odbicia w linii długiej
W linii jednorodnej fala wsteczna może ulec odbiciu od końca linii (na obiążeniu­odbiorniku). Stosunek amplitudy fali odbitej do A2
amplitudy fali padającej określony jest przez współczynnik odbicia: ρ=
A1
u→ ( x ,t )
i→ ( x , t )
u← ( x ,t )
i← (x , t)
u→ +u←
Na podstawie prawa Ohma: Z obc=
i→ +i←
u→
ρ=
Pondto współczynnik odbicia:
u←
A
dostajemy:
1
u←
1+
1+ρ
u→ +u← u→
u→
Z obc=
=
=
i→ +i← 1
i → i ← u← 1 ρ
+
+
u→ u→ u← u→ Z 0 Z 0
w.6, p.13 ρ=
Z obc −Z 0
Z obc +Z 0
Odbicia sygnałów w linii długiej
Z obc−Z 0
ρ=
Z obc + Z 0
Wyróżniamy trzy przypadki szczególne:
1. Z obc =Z 0 → ρ=0
Mówimy, że linia jest prawidłowo obciążona (dopasowana). Nie ma odbić, sygnał tylko od nadajnika (np.: detektor cząstek)
2. Z obc =∞ → ρ=1
Sygnał na końcu linii odbija się z taką samą amplitudą, nakłada się na sygnał ze źródła­zniekształcenie sygnału (informacji) z nadajnika.
3.
Z obc =0 → ρ=−1
Sygnał na końcu linii odbija się całkowicie z inwersją, nakłada się na sygnał ze źródła­zniekształcenie informacji z nadajnika.
w.6, p.14 Linia długa – przekaz mocy, opóźnienie sygnałów
Z0
ZW rezystancja Zobc rezystancja wewnetrzna
nadajnika
obciążenia
Aby nie było odbić musi być Zobc=Z0. W linii bez strat sygnały są przenoszone bez tłumienia i zniekształceń. Dla uzyskania maksymalnego przekazu mocy musi być spełniony warunek ZW=Z0.
Do przesyłania sygnałów stosuje się najczęściej kable koncentryczne. Są one tak
wykonywane aby: Z0 kilkadziesiąt – kilkaset omów, typowo 50 , 75  L
Z
≃
0
C
( √ )
Opóźnienie sygnałów w linii długiej (czasami wykorzytywane do formowania impulsów):
l
1
t =l √ LC
vf=
; t=
vf
LC
√
Typowe kable dają opóźnienie impulsów 5 ns/m.
w.6, p.15 Sprzężenie zwrotne, wzmacniacz operacyjny w.6, p.16 Sprzężenie zwrotne
Sprzężeniem zwrotnym nazywa się oddziaływanie skutku na przyczynę.
Regulator odśrodkowy w maszynie parowej (James Watt 1788)
w.6, p.17 Sprzężenie zwrotne
W elektronice sprzężenie zwrotne pozwala projektować układy o określonych własnościach. Stosuje się je dla wzmacniaczy. Wzmacniacz
Wzmacniacz ze sprzężeniem zwrotnym
Część sygnału wyjściowego βu2, zwana w.6, p.18 sygnałem zwrotnym, zostaje skierowana do wejścia układu i zsumowana z
sygnałem wejściowym.
Sprzężenie zwrotne (przypadek K>0, β<0 lub β>0)
Kt
Układ równoważny do tego po lewej stronie slajdu Dla węzła sumującego: u=u1 +β u2
u2 =K u=K (u 1 +βu 2)
K
u1
czyli: u2 =
(1−β K )
a nowe wzmocnienie Kt:
u2
K
Kt= =
u1 (1−β K)
w.6, p.19 Jeżeli wzmocnienie K jest bardzo duże, tak że ∣K∣ >> 1, to wzmocnienie całkowite takiego układu jest określone przez układ sprzęgający i nie zależy od K: 1
K t ≃− β
Przykład realzacji sprzężenia zwrotnego
Dzielnik napięcia jako układ sprzęgający:
βu 2
u2
βu 2
u2
R1=1 k Ω
R2 =10 k Ω
zatem:
niech K=100000
K
105
10 5
Kt=
=
=
=9.9995≈10
5
−1
1+β K 1+10 ⋅10
10001
zmieniamy K o 100%, K=200000
K
2⋅10 5
2⋅105
Kt=
=
=
=9.9995≈10
1+β K 1+2⋅105⋅10−1 20001
Wzmocnienienie układu zmieniło się jedynie o 0.005%!
w.6, p.20 Sprzężenie zwrotne
Można wyróżnić trzy podstawowe przypadki sprzężenia zwrotnego:
Kt=
1
1
−β
K
w.6, p.21 1) β<0 – ujemne sprzężenie zwrotne 2) 0<β<1/K – dodatnie sprzężenie zwrotne
3) β=1/K – Kt →∞. Sprzężenie zwrotne
Ujemne:
Fazy sygnału wejściowego i sygnału sprzężenia zwrotnego są przeciwne ( <0). Całkowite wzmocnienie układu mniejsze od wzmocnienia samego wzmacniacza.
­ duża stabilność pracy układu. ­ parametry układu ze wzmacniaczem o dużym wzmocnieniu zależą wyłącznie od parametrów układu sprzężenia zwrotnego, a te mogą być bardzo stabilne
(układy sprzęgające buduje się często tylko z elementów biernych). ­ zmniejszają się szumy i zniekształcenia sygnałów. ­ zwiększa się górna częstotliwość graniczna (szersze pasmo przenoszenia).
­ modyfikacja impedancji wejściowej i wyjściowej.
w.6, p.22 Sprzężenie zwrotne
Dodatnie:
Fazy sygnału wejściowego i sygnału sprzężenia zwrotnego są zgodne ( >0).
Efektywne wzmocnienie ulega zwiększeniu. Układy z K < 1 stosuje się rzadko z uwagi na małą stabilność pracy oraz wzrost zniekształceń sygnałów.
Przypadek szczególny: jeżeli K → 1 to oczekujemy, że wzmocnienie dążyć będzie do nieskończoności. W rzeczywistości wzrost wzmocnienia jest ograniczony – sygnał wyjściowy nie może być większy niż napięcie zasilające wzmacniacz. W układach takich dzięki silnemu sprzężeniu następuje generacja drgań co wykorzystywane jest do budowy generatorów.
w.6, p.23 Wzmacniacz operacyjny ­ historia
­ lata 20­te XX w. zauważono, że wzmacniacz oraz odpowiedni układ rezystorów, kondensatorów umożliwia wykonywanie prostych operacji matematycznych: +, ­.
­ następnie rozwinięto tę technikę na tyle, że można było wykonywać bardziej złożone operacje matematyczne (komputer analogowy): d
,
dt
∫ ... dt ,
/, ⋅... ,
log (...),
etc .
­ WW2 – liczenie trajektorii pocisków etc. ­ w latach 40­tych pierwszy lampowy wzmacniacz, wtedy też uznano nazwę wzmacniacz operacyjny.
1967 – pojawia się pierwszy monolityczny wz. op. 741
w.6, p.24 Wzmacniacz operacyjny ­ zastosowania
w.6, p.25 Wzmacniacz operacyjny Wzmacniacz operacyjny jest to wzmacniacz o bardzo dużym wzmocnieniu napięciowym (AOL), który posiada dwa wejścia =+15 V
i jedno wyjście. Jedno z wejść (­­) nosi nazwę odwracającego
– sygnał wyjściowy jest przesunięty w fazie o 180o względem sygnału przyłożonego do tego wejścia. Drugie −15 V =
wejście (+) nazywa się nieodwracającym – sygnał albo:
wyjściowy jest zgodny w fazie z sygnałem podanym na to wejście. Wzmacniacz operacyjny realizuje funkcję:
v o= A OL (v + −v − )
Wzmacniacz operacyjny jest przeznaczony zwykle do pracy z zewnętrznym obwodem sprzężenia zwrotnego, które decyduje o głównych własnościach
całego układu. w.6, p.26 vo
Idealny wzmacniacz operacyjny
Posiada następujące własności:
nieskończenie duże wzmocnienie napięciowe Aol=∞, nieskończenie duża rezystancja wejściowa Rin=∞, rezystancja wyjściowa równa zeru Rout=0, nieskończenie szerokie pasmo przenoszenia częstotliwości (od 0 do ∞), Pamiętając o powyższch własnościach WO (wzmacniacz operacyjny) można przeprowadzać prostą (lecz dokładną) analizę działania obwodów zbudowanych na jego bazie.
w.6, p.27 Wzmacniacz operacyjny ­ obwód zastępczy
­ na podstawie cechy Rin=∞ : WO nie pobiera prądu, iin=0
­ na podstawie równania WO: obwód wyjściowy można przedstawić jako VCVS ­ źródło napięcia sterowane napięciem (v+­v­)
­ na podstawie cechy Rout=0 : to źródło napięcia jest idealne (napięcie na wyjściu nie zależy od obciążenia)
­ na podstawie cechy Aol=∞ : v+=v­ ponieważ:
vo
skończony
( v + −v− )=
=
=0
A OL nieskończony
i input=0
w.6, p.28 Rzeczywisty wzmacniacz operacyjny ­ wzmocnienie napięciowe w typowych wzmacniaczach AOL = 104 – 107, w specjalistycznych do 1010, ­ górna granica pasma przenoszonych częstotliwości kilkadziesiąt MHz, ­ impedancja wejściowa 104 – 1013 Ω, ­ impedancja wyjściowa kilkadziesiąt WΩ, ­ maksymalna szybkość narastania napięcia wyjściowego rzędu kilku, kilkudziesięciu V/μs, ­ napięcie wyjściowe jest ograniczone, zwykle mniejsze o 1 – 2 V od napięcia zasilania, ­ parametry wzmacniacza zależą od temperatury. Stąd obwód zastępczy:
w.6, p.29 Rzeczywisty wzmacniacz operacyjny ­wysycenie Sygnały wyjściowy vs. sygnał wejściowy
Wysycenie typowo: 12­15 V.
Obszar pracy liniowej
Przykład dla sygnału wejściowego typu sinusoidalnego:
w.6, p.30 Przykład ­ wzmacniacz operacyjny 741
20 tranzystorów
11 rezystorów
1 kondensator
w.6, p.31 Przykład ­ wzmacniacz operacyjny 741
stosowany na Studenckiej Pracowni Elektronicznej i nie tylko
w.6, p.32 Wzmacniacz nieodwracający fazy
AOL=∞
Sygnał wejściowy:
Sygnał wyjściowy:
wzmocnienie > 1
β
R2
v 0= 1+
vi
R1
( )
Sygnał wejściowy:
Korzystając ze wzoru na sprzężenie zwrotne:
R2
1
v 0=K L v i= v i = 1+
vi
β
R1
( )
Impedancja wejściowa tego wzmcniacza jest: ∞ w.6, p.33 Wzmocnienie = 1
Sygnał wyjściowy:
Wzmacniacz nieodwracający fazy – analiza układu
Idealny WO. Na wyjściu napięcie skończone (ujemne sprzężenie) zatem różnica potencjałów między wejsciem (+) i (­) wynosi 0. Na podstawie (1) vi­=vi.
Z prawa Ohma prąd przez rezystow R1 wynosi: i1=vi/R1
Impedancja wejsciowa WO nieskończona → prąd (­) =0A
Z prawa KCL prąd dla rezystora R2: i2=i1=vi/R1 Spadek napięcia na rezystorze R2 (prawo Ohma) wynosi vR2=i2R2=R2/R1vi
Z prawa KVL sumaryczny spadek napięcia na rezystorach R2 i R1:
R2
R2
v 0=v i + v i= 1+
vi
w.6, p.34 R1
R1
( )
Przykład projektowania­ wzmacniacz nieodwracający fazy
Chcemy uzyskać wzmacniacz o wzmocnieniu: KL=5V/V
R2
Na podstawie wzoru: K L =1+
R1
Wybieramy: R1= 1kΩ i R2=4kΩ
Po dołączeniu dowolnego źródła sygnału, specyfikacja jest ciągle spełniona bo i=0A.
w.6, p.35