Zasilacze impulsowe - KONWERTER OBNIŻAJĄCY NAPIĘCIE
zasada działania, sposób projektowania, przykład obliczeń
Maciej Radtke
wersja 1.01, z 9 lutego 2011 r.
zauważone błędy proszę zgłaszać na adres:
[email protected]
1. Po co nam zasilacz impulsowy?
No właśnie - po co?
Jakiś czas temu, w odpowiedzi na prośbę o zaprojektowanie zasilacza impulsowego, obniżającego
napięcie z 20 na 5 V przy przewidywanym prądzie obciążenia do 1 A, usłyszałem pytanie: czy – zamiast
się męczyć i projektować przetwornicę – nie można użyć gotowego stabilizatora liniowego, na przykład
popularnego 7805? Zamiast skomplikowanych obliczeń, nawijania cewki i budowania generatora,
kupujemy jeden tani układ scalony, „obudowujemy” go dwoma kondensatorami i gotowe. Dane
katalogowe wspomnianego stabilizatora pokazują, że wytrzyma on prąd obciążenia 1 A (maksymalny prąd
wyjściowy układu 7805 to 1,5 A).
Policzmy: jeśli napięcie wyjściowe naszego prościutkiego liniowego zasilacza ma być równe 5 V,
a pobierany prąd 1 A, moc odbierana z wyjścia to okrągłe 5 W. A jaka jest moc dostarczana do jego
wejścia? To proste: 20 V x 1 A = 20W (a nawet ciut więcej, bo przecież stabilizator 7805 dodatkowo
„zeżre” nieco prądu na zasilanie swoich wewnętrznych układów). A więc sprawność naszego „liniowca” to
zaledwie 25%! Inaczej mówiąc, jeśli zbudujemy zasilacz liniowy, wyślemy w kosmos przeszło trzy razy
więcej energii niż ta, którą zużyjemy. To jest po pierwsze mało opłacalne ekonomicznie, a po drugie – co
często bywa poważniejszym problemem – traconą energię (w opisywanym przykładzie tylko 15 W, ale
proszę sobie wyobrazić podobny zasilacz nie na 1, a na 10A) trzeba rozproszyć w postaci ciepła. I to już
może być bardzo poważny problem oraz konieczność zastosowania potężnego (czyli bardzo dużego
i drogiego) radiatora. Ostatecznie nasz, niby prosty, zasilacz liniowy nie będzie ani mały, ani bardzo łatwy
do zaprojektowania (dobieranie radiatorów to nie jest najprzyjemniejsze zajęcie).
Na tym etapie rozważań proszę czytelnika, aby przyjął na wiarę (dalej to uzasadnię): dobrze
zaprojektowany zasilacz impulsowy może mieć, niezależnie od napięć na jego wejściu i wyjściu, sprawność
sięgającą 80-90%. Czyli w naszym przykładzie straty mocy można zredukować z przeszło 15 do nie więcej
niż 3 W, co najmniej pięciokrotnie. Jest więc o co powalczyć.
2. Jak to się robi – czyli wiadomości ogólne, podstawowa struktura i zasada działania
konwertera obniżającego napięcie
2.1 Jak go zwał...
Na początek uporządkujmy nazewnictwo. „Serce” zasilacza impulsowego to impulsowy konwerter
napięcia (czasem: konwerter DC-DC) – układ składający się z cewki, kondensatora i elektronicznych
kluczy, którego zadaniem jest prawie bezstratne przetwarzanie jednego napięcia na inne.
Znane są trzy podstawowe typy konwerterów: obniżający napięcie (step-down), podwyższający
napięcie (step-up) i odwracający polaryzację napięcia (z jego jednoczesnym podwyższeniem lub
obniżeniem).
Zamiennie z konwerterem bywa używane określenie przetwornica, ale ja raczej skłaniam się do
nazywania przetwornicą bardziej złożonego układu, zbudowanego z konwertera oraz z generatora, którego
zadaniem jest sterowanie i przełączanie kluczy w konwerterze. A jeśli do przetwornicy dodamy kolejne
układy, przeznaczone do zapewnienia stabilizacji napięcia wyjściowego, powstanie nam kompletny,
stabilizowany zasilacz impulsowy. Oczywiście może to być zasilacz obniżający, podwyższający lub
zmieniający polaryzację napięcia.
Istnieje jeszcze kilka, używanych w literaturze, nazw. Układ obniżający napięcie bywa nazywany
konwerterem przepustowym (forward converter), konwerterem współbieżnym lub konwerterem
jednotaktowym, a układ podwyższający – konwerterem zaporowym (flyback converter), przeciwbieżnym
albo dwutaktowym. [@tabelka]
1
2.2 Jak to wgląda
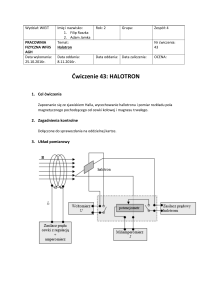
Podstawowy schemat konwertera obniżającego pokazuje rys. 1a. Zamknięcie klucza K1 powoduje
doprowadzenie do cewki L porcji energii (ze źródła napięcia wejściowego UI), której część jest od razu
przekazywana (przez uzwojenie) do obciążenia, a część magazynowana w rdzeniu cewki w postaci energii
pola magnetycznego. Po otwarciu klucza obciążenie „korzysta” z tej zmagazynowanej energii, dzięki
czemu jest możliwe utrzymanie ciągłości prądu płynącego do obciążenia. Zadaniem kondensatora C jest
„wygładzenie” i zapewnienie stałości napięcia wyjściowego UO. Klucz K2 jest włączany naprzemiennie
z kluczem K1 (K1 włączony – K2 wyłączony i odwrotnie), a jego zadaniem jest zamknięcie obwodu dla
płynącego prądu wtedy, gdy cewka zostaje odłączona od napięcia UI. Okresowe doprowadzanie energii do
cewki przy jednoczesnym ciągłym jej odbiorze
z wyjścia
konwertera
umożliwia
teoretycznie
bezstratne przekazanie mocy z wejścia na wyjście,
mimo iż napięcie UI jest wyższe od napięcia UO.
Bardzo ważne jest, by oba klucze były
przełączane jednocześnie i by nigdy nie było sytuacji,
kiedy oba są w tym samym stanie (oba włączone lub
oba wyłączone). Jednoczesne włączenie obu kluczy
powodowałoby zwarcie źródła napięcia wejściowego
bezpośrednio do masy, zaś ich równoczesne
wyłączenie – nagłe odłączenie jednej z końcówek
cewki od jakiegokolwiek obwodu, co spowodowałoby
powstanie na niej przepięcia o niekontrolowanej
(ogromnej, teoretycznie nieskończonej) wartości.
Nietrudno zauważyć, że taki układ jest bardzo
trudny do zrealizowania i właściwie może działać
poprawnie tylko na papierze (problem wynika m. in.
Rys. 1: Schemat konwertera obniżającego
ze skończonej i zawsze niejednakowej szybkości
napięcie.
przełączania rzeczywistych kluczy).
Układ z rys. 1b przedstawia praktyczną,
typową realizację opisywanego konwertera i tym się różni od poprzedniego, że sterowany (przełączany)
jest tylko jeden klucz – tranzystor Q. Drugi klucz, dioda D, przełącza się „automatycznie” - włącza się
(zaczyna przewodzić) na skutek wyłączenia tranzystora, a wyłącza się, gdy tranzystor zostaje włączony
(nasycony).
2.3 Jak to działa
Na początku poczynimy następujące założenia:
•
•
•
•
W układzie panuje stan ustalony. Znaczy to, że konwerter został uruchomiony odpowiednio dawno,
kondensator C został naładowany do pewnej ustalonej wartości napięcia U O (niższej od napięcia UI), a jego
pojemność jest na tyle duża, że to napięcie jest praktycznie stałe (i praktycznie niezależnie od np. prądu
obciążenia). Do obciążenia płynie stały prąd I O. Prąd ten może przybierać różne wartości, od 0 mA do
określonego prądu maksymalnego IOMAX.
Do bazy tranzystora Q jest doprowadzony sygnał sterujący ST, który ten tranzystor okresowo
włącza (nasyca), albo go wyłącza. Zakładamy (w znakomitej większości przypadków to założenie
jest słuszne), że tranzystor nasycony stanowi idealne zwarcie i pomiędzy jego kolektorem
i emiterem nie występuje żaden opór ani spadek napięcia. Oczywiście tranzystor wyłączony jest
idealnym rozwarciem.
Nieprzewodząca dioda D stanowi idealne rozwarcie, a przewodząca – idealne zwarcie. Od tego
założenia niekiedy należy uczynić odstępstwo (czyli uwzględnić spadek napięcia na przewodzącej
diodzie), ale najczęściej jego przyjęcie nie powoduje pojawienia się wielkich błędów.
Cewka i kondensator zachowują się jak cewka i kondensator (jeśli ktoś nie pamięta, jak zachowują
się te elementy, niech zajrzy do dodatku 1).
Na rys. 2 zostały pokazane czasowe przebiegi napięć i prądów, charakterystyczne dla opisywanego
konwertera. Pierwszy przebieg, oznaczony jako U C(t), obrazuje napięcie, które pojawia się na kolektorze
tranzystora Q. Na tym rysunku zaznaczono, kiedy tranzystor Q jest włączony (nasycony), a kiedy jest
wyłączony. Włączanie tranzystora powtarza się cyklicznie co okres T i trwa przez czas δT (parametr δ jest
nazywany współczynnikiem wypełnienia impulsów sterujących). W czasie od δT do T tranzystor jest
wyłączony.
2
Nietrudno zauważyć, że w czasie od 0 do
δT, gdy tranzystor jest nasycony i – zgodnie
z przyjętym założeniem – stanowi zwarcie,
napięcie na jego kolektorze jest równe napięciu
wejściowemu UI. To napięcie jest wówczas
przyłożone do lewej końcówki cewki L,
a jednocześnie na jej prawej końcówce panuje
stałe napięcie UO (patrz: założenia!). Tak więc
przez czas 0...δT do cewki jest przyłożone stałe
napięcie UL1 = UI – UO. Stałe napięcie,
przyłożone
do
cewki,
powoduje
liniowe
narastanie płynącego przez nią prądu, co można
opisać równaniem:
i L t=I L0
U L1
U −U O
t=I L0 I
t
L
L
(1)
Jako że dioda jest wyłączona (bo na jej
katodzie jest napięcie wyższe, niż na anodzie),
w czasie od chwili 0 do δT prąd cewki jest
identyczny z prądem kolektora tranzystora Q.
Przez czas δT prąd cewki przyrasta o:
I L=
U I −U O
T
L
(2)
Tu bardzo ważna uwaga: jeśli przed
chwilą 0 (włączeniem tranzystora) prąd w cewce
nie płynął, prąd ILK w chwili δT jest równy Δi L,
natomiast jeśli początkowy prąd cewki był
niezerowy i równy IL0, prąd w chwili δT jest
Rys. 2: Przebiegi czasowe prądów w konwerterze
równy ILK = IL0 + ΔiL (oba przypadki zostały
obniżającym napięcie.
pokazane na rysunku).
Czas, kiedy tranzystor Q jest włączony
(od chwili 0 do δT), jest nazywany czasem pompowania (ładowania) cewki lub taktem wejściowym
konwertera.
W chwili δT następuje wyłączenie tranzystora, jednak przez cewkę prąd płynie nadal (cewka
zachowuje się jak źródło prądowe o chwilowej wydajności I LK). Ten prąd nie może nagle „zniknąć”, a przez
wyłączony tranzystor dalej przepływać nie może. W tej sytuacji jedyną drogą dla prądu jest dioda D, która
w chwili δT się włącza, zaczyna przewodzić, i przejmuje prąd cewki dotychczas płynący przez tranzystor.
W ten sposób dioda zostaje „automatycznie włączona” przez wyłączający się tranzystor Q. Mamy tu więc
pewne, naprzemienne włączanie i wyłączanie się kluczy.
Jaki jest rozkład potencjałów na końcówkach cewki po włączeniu się diody? Zgodnie z przyjętymi
założeniami: na prawej końcówce cewki cały czas panuje napięcie UO, natomiast na końcówce lewej
„nowe” napięcie to ok. 0 V (a dokładnie: -UF, czyli <minus>napięcie przewodzenia diody). A więc do cewki
znów jest przyłożone napięcie stałe, tyle że skierowane przeciwnie niż poprzednio. Jest ono teraz równe
UL2 = -UO. To napięcie, działając przez czas (T – δT), powoduje zmianę prądu w cewce o:
− I L=
−U O
T − T
L
(3)
Teraz prąd w cewce (tym razem identyczny z prądem diody D) liniowo maleje, poczynając od
wartości ILK (czyli od prądu, który płynął przez cewkę w chwili wyłączenia tranzystora i włączenia diody) do
IL0 (ten prąd będzie wartością początkową prądu cewki w chwili ponownego włączenia tranzystora - patrz
rys. 2). Stąd znak minus po lewej stronie równania.
Oczywiście, jeśli w układzie mamy stan ustalony (a jeżeli nie mamy, to czekamy tak długo , aż się
on pojawi), zmiana prądu cewki ΔI L w tym takcie – zwanym taktem wyjściowym – musi być taka sama,
jak zmiana prądu cewki ΔI L w poprzedzającym go takcie wejściowym (można powiedzieć, że w chwili T
prąd cewki „wraca” do takiego, jaki płynął w chwili 0).
3
Możemy więc zapisać następującą „oczywistą oczywistość”:
U I −U O
U
T = O T − T
L
L
(4)
skąd, po prostych przekształceniach, otrzymujemy podstawową zależność wiążącą napięcia na
wejściu i wyjściu konwertera obniżającego napięcie:
U O= U I
(5)
Widać, że napięcie na wyjściu konwertera zależy wyłącznie od napięcia wejściowego
i współczynnika wypełnienia impulsów sterujących, natomiast nie zależy ani od indukcyjności cewki, ani od
częstotliwości przełączania kluczy.
2.4 Kiedy to działa źle
Przyjrzyjmy się jeszcze raz schematowi konwertera, a dokładniej – płynącym w nim prądom. Łatwo
zauważyć, że płynący do obciążenia prąd I O jest równy średniemu prądowi cewki (rolę „uśredniacza” pełni
odpowiednio duży kondensator C), a jako że prąd cewki naprzemiennie (i liniowo) przyrasta i maleje o tę
samą wartość, IO „leży w połowie” ΔIL, czyli:
I O=I L0
IL
I
=I LK − L
2
2
(6)
Obrazuje to rys. 3a, na którym pokazano przykładowe przebiegi prądu I L dla różnych wartości
prądu IO. Widać, że w miarę zmian prądu obciążenia przebieg prądu cewki „wędruje” w górę i w dół, nie
zmieniając kształtu. To jest oczywiste, jeśli się przeanalizuje rozważania z poprzedniego rozdziału –
przecież nachylenia zmian IL nie zależą od
IO!
Szczególną uwagę należy zwrócić na
sytuację, kiedy IL0 = 0. Dzieje się to wtedy,
gdy prąd IO osiąga pewną określoną
wartość IOKR. Jest ona na pewno większa od
zera. Zastanówmy się teraz co się stanie,
gdy prąd IO zostanie zmniejszony poniżej
tej wartości. Aby nadal była spełniona
zależność:
I O=I LŚR
(7)
(a ta zasada jest w układzie konwertera
step-down „święta”)
musiałoby być:
I L0 0
(8)
co jest niemożliwe, bo ani przez tranzystor,
ani przez diodę nie może popłynąć ujemny
(wsteczny)
prąd.
Czyli
mechanizm
zmniejszania prądu ILŚR musi być inny.
Zastanówmy się, jaki? Od razu zauważymy,
że jeśli IL0 nie może przybierać wartości
ujemnych, to musi się zmniejszyć ILK. Ale
ponieważ:
I LK =
U I −U O
T
L
(9)
Rys. 3: Prąd w cewce przy obciążeniach: nadkrytycznym
(a), krytycznym (a, b) i podkrytycznym (b).
a wielkości: UI, L oraz δT zmienić się nie
mogą, zmienia się UO. Jak? Rośnie.
4
Na rys. 3b został pokazany przebieg i L(t) dla takiej właśnie sytuacji – gdy prąd I O jest mniejszy od
IOKR. W takcie wejściowym do cewki jest przyłożone napięcie mniejsze niż U I – (założone)UO , a w takcie
wyjściowym – napięcie od założonego U0 wyższe. W takiej sytuacji w czasie od 0 do δT prąd cewki narasta
wolniej, a w czasie od δT do T szybciej opada, osiągając zerową wartość jeszcze przed zakończeniem
pełnego cyklu pracy konwertera. Prąd cewki płynie więc w sposób nieciągły.
Reasumując: jeśli konwerter zostanie obciążony prądem mniejszym, niż tzw. prąd krytyczny IOKR
(czyli taki, przy którym prąd w cewce „dotyka” w jednym punkcie na osi czasu wartości 0), zależność
UO = δUI przestaje obowiązywać i napięcie wyjściowe jest wyższe od założonego. Dla prądu obciążenia
IO = 0 napięcie na wyjściu konwertera typu step-down jest takie samo jak na jego wejściu.
To jest bardzo ważna cecha wszystkich impulsowych konwerterów DC-DC, w sposób istotny
różniąca je od zasilaczy o pracy ciągłej – jeśli nie zastosuje się dodatkowych układów zabezpieczających,
działają poprawnie tylko dla pewnego przedziału prądów obciążenia, a zmniejszenie I O poniżej IOKR
skutkuje wzrostem napięcia na wyjściu. W krańcowym przypadku może to nawet doprowadzić do
uszkodzenia zasilanego układu lub do uszkodzenia samego konwertera (napięcie nie obciążonego
konwertera typu step-up rożnie teoretycznie aż do nieskończoności!).
3. Jak to się projektuje – etap 1
3.1 Napięcie wyjściowe i współczynnik wypełnienia δ
Jak zostało powiedziane wcześniej, najczęściej możemy poczynić założenie, że spadki napięć na
przewodzącej diodzie i nasyconym tranzystorze są do pominięcia. Wówczas, znając napięcie wejściowe
i założone napięcie na wyjściu konwertera, możemy obliczyć współczynnik wypełnienia impulsów
sterujących δ:
=
UO
UI
(10)
Czy zawsze możemy pominąć UF (napięcie przewodzenia diody) i UCES (napięcie nasycenia
tranzystora)?
Z napięciem nasycenia tranzystora sprawa jest łatwiejsza: nasycony tranzystor jest włączony
w szereg z napięciem wejściowym (wyższym), więc pominięcie U CES na ogół nie powoduje wielkiego błędu
(chyba że stosujemy tranzystory w układzie Darlingtona lub budujemy układ, w którym przez tranzystor
będą płynęły bardzo duże prądy – wtedy napięcie nasycenia może być spore, rzędu 1 V i więcej).
Pominięcie napięcia przewodzenia diody może powodować sporą niedokładność obliczenia
współczynnika δ wtedy, kiedy napięcie wyjściowe konwertera jest niewielkie. Jednak przy małych
napięciach wyjściowych bardzo często stosuje się nie zwykłe diody P-N, a diody Schottky'ego, których
napięcie przewodzenia jest wyraźnie niższe (około 0,2 – 0,3 V). A więc najczęściej uwzględnianie spadków
napięć na kluczach jest bezcelowe. Osoby bardzo dokładne mogą zajrzeć do dodatku 2, w którym są
zamieszczone dokładne wyliczenia, z uwzględnieniem napięć UF oraz UCES.
3.2 Dobór częstotliwości pracy konwertera
Częstotliwość przełączania tranzystora nie ma bezpośredniego wpływu na wielkość napięcia na
wyjściu konwertera, a więc w pierwszym przybliżeniu można ją wybrać dowolnie. Najczęściej, jeśli nie ma
innych ograniczeń, wybiera się częstotliwość powyżej zakresu słyszalności, czyli powyżej 20 kHz. Zasilacze
impulsowe, pracujące na niskich częstotliwościach, wydają nieprzyjemny i uciążliwy pisk, powodowany
m. in. magnetostrykcją (czyli zmianą wymiarów ferrytu pod wpływem zmiennego pola magnetycznego)
rdzenia cewki.
Częstotliwości pracy konwertera nie można jednak zwiększać nieograniczenie, bowiem
w konwerterach impulsowych stosuje się cewki z rdzeniem (ferrytowym), a wraz ze wzrostem
częstotliwości stratność ferrytów się zwiększa. Ta zależność jest nieliniowa i dla każdego typu ferrytu
można określić maksymalną częstotliwość, powyżej której dany materiał nie powinien być używany.
Stosowne dane należy odszukać w katalogach. Przykładowe charakterystyki strat w ferrytach, także w
zależności od częstotliwości ich przemagnesowywania, zostały zamieszczone w dodatku 3.
Ważnym ograniczeniem dla zwiększania częstotliwości pracy konwertera jest też ograniczona
szybkość przełączania kluczy (a zwłaszcza tranzystorów). Jeśli czas przełączania (tranzystora lub diody)
przestaje być wyraźnie mniejszy niż czas trwania któregoś z taktów pracy konwertera, należy się liczyć
5
z wyraźnym wzrostem strat (w bilansie mocy odbieranej z konwertera i mocy do niego dostarczanej
znaczący
staje
się
udział
strat
związanych
z
przełączaniem
zastosowanych
elementów
półprzewodnikowych).
Typowy zakres częstotliwości pracy impulsowych konwerterów napięcia to kilkanaście - kilkadziesiąt
kiloherców.
3.3 Obliczanie indukcyjności cewki
Punktem wyjścia dla obliczenia indukcyjności cewki są rozważania z rozdziału 2.4. Przede
wszystkim musimy się zastanowić, jaki najmniejszy prąd (tak, właśnie najmniejszy prąd jest punktem
wyjścia do obliczeń) będziemy chcieli pobierać z projektowanego układu. Ten prąd będzie jego prądem
krytycznym. Przypomnijmy: IO = ILŚR (7), a dla prądu krytycznego:
I OKR=I LŚR=
IL
2
(11)
i jednocześnie:
I L=
U I −U O
U − U I
T= I
T
L
L
(12)
skąd, po podstawieniu i przekształceniu, otrzymujemy:
L=
U I 1−
2fI OKR
(13)
gdzie f = 1/T – częstotliwość pracy konwertera.
Podsumowując: indukcyjność cewki L liczymy „na minimalny prąd wyjściowy konwertera”, przy
wcześniej założonym napięciu wyjściowym i częstotliwości.
Warto zauważyć, że częstotliwość f i prąd krytyczny I OKR są wymienne – przy danej indukcyjności
cewki możemy zmniejszyć prąd krytyczny, zwiększając częstotliwość pracy konwertera, i odwrotnie.
Należy jednak mieć zawsze na uwadze ograniczenia wspomniane wcześniej – wzrost strat w rdzeniu wraz
ze wzrostem częstotliwości jego przemagnesowywania oraz ograniczoną szybkość przełączania kluczy
elektronicznych (tranzystorów i diod).
Należy też być ostrożnym przy zwiększaniu ponad miarę indukcyjności L (im większa indukcyjność
cewki, tym mniejszy prąd krytyczny konwertera). Cewka o większej indukcyjności oznacza nie tylko
większe jej wymiary, ale także więcej zwojów, czyli dłuższy drut. A dłuższy drut przekłada się na większą
rezystancję, a więc większe straty. Należy też pamiętać, że większych częstotliwościach zaczyna się
pojawiać efekt naskórkowości, przez co efektywna rezystancja drutu ulega zwiększeniu (prąd płynie tylko
po jego powierzchni). Środkiem zaradczym może być nawinięcie cewki zwane bifilarnym, czyli
jednocześnie (równolegle) kilkoma izolowanymi od siebie drutami o mniejszej średnicy. Niestety dla
niewprawnej osoby wykonanie takiego uzwojenia może być sporym utrudnieniem.
3.4 Dobór kondensatora
Występowanie tętnień napięcia na wyjściu impulsowego konwertera napięcia jest jego naturalną
cechą, wynikającą z nieustannych zmian prądu w cewce. Tętnienia te mają częstotliwość f = 1/T
i, niestety, dosyć złożony kształt (nie są sinusoidalne!). To sprawia, że ich całkowite wyeliminowanie nie
jest łatwe, można je natomiast wydatnie zredukować stosując wyjściowy kondensator C o odpowiednio
dużej pojemności. Jego zadaniem jest „wygładzenie” napięcia wyjściowego i uśrednienie zmieniającego się
prądu cewki do stałego prądu IO.
Obliczanie wymaganej pojemności kondensatora należy rozpocząć od założenia dopuszczalnej
amplitudy1 tętnień. Tu ważna uwaga: nie istnieje jakaś uniwersalna wielkość tętnień, którą można by
uznać za optymalną w każdym przypadku. Tętnienia o amplitudzie 100 mV mogą być uznane za małe,
jeśli napięcie UO będzie wynosiło 20 V (stanowią wówczas 0,5% tego napięcia), ale na pewno będą
1
Jest pewien bałagan w sposobie używania i znaczeniu tego słowa. Jeśli się mówi o sinusoidzie, „amplituda” znaczy zawsze
połowę wartości międzyszczytowej sinusa, ale w przypadku prostokąta amplituda to jego całkowita „wysokość - czyli napięcie pp. Tutaj mamy do czynienia z przebiegiem jeszcze bardziej złożonym - niesinusoidalnym i do tego niesymetrycznym względem
osi czasu. Przyjęto więc zasadę, że pod pojęciem „amplituda tętnień” należy rozumieć ich wartość międzyszczytową.
6
ogromne względem UO = 2V (5%). Z drugiej strony, tętnienia o amplitudzie 5% U O mogą nie przeszkadzać
przy zasilaniu żarówki, ale w innym przypadku tętnienia półprocentowe mogą sprawić, że projektowany
zasilacz nie będzie się nadawał do zasilenia precyzyjnego wzmacniacza pomiarowego. To, jaka wartość
zostanie przyjęta, zależy od indywidualnych wymagań postawionych osobie projektującej konwerter.
Na wstępie trzeba zaznaczyć, że bardzo dokładne obliczenie pojemności potrzebnego kondensatora
jest ogromnie trudne. Na szczęście, jeśli się na problem popatrzy praktycznie, można przyjąć założenia
radykalnie upraszczające obliczenia. Ma to sens także dlatego, że obliczoną wartość pojemności i tak
najczęściej traktuje się jako minimalną, a do rzeczywistego układu wmontowuje kondensator
o pojemności większej.
Zakładamy więc, że:
•
•
•
Będziemy dobierali kondensator przy założeniu, że tętnienia są małe (do kilku procent U O). Im
założone tętnienia będą większe, tym mniejsza będzie dokładność wyliczeń.
Do obciążenia płynie stały prąd IO.
Konwerter pracuje w zakresie obciążeń nadkrytycznych (IO > IOKR).
Popatrzmy na rys. 4, przedstawiający prąd cewki i, odpowiadający mu, prąd I O. Z prawa Kirchhoffa:
I C =I L−I O
(14)
Nietrudno zauważyć, że pomiędzy
chwilami t1 i t2 prąd do kondensatora
wpływa a pomiędzy t2 i t3 z niego
wypływa. Jako że średnia wartość napięcia
na kondensatorze to UO (jest ona prawie
stała – patrz założenia!), wpływające
i wypływające porcje prądu powodują na
przemian
niewielkie
doładowywanie
i rozładowywanie kondensatora – to są
właśnie tętnienia, które pojawiają się na
wyjściu konwertera, na tle napięcia
wyjściowego.
Jak
obliczyć
amplitudę
tych
tętnień? Zauważmy, że prąd wpływający
doładowuje kondensator o tyle, o ile
zostanie on później rozładowany przez
prąd z niego wypływający. Wystarczy więc
obliczyć
przyrost
napięcia
na
kondensatorze w czasie t1 – t2 (lub jego
spadek w czasie t2 – t3), by poznać
amplitudę tętnień.
Przyjrzyjmy się rysunkowi: chwila
t1 leży w połowie czasu pomiędzy 0 a δT,
a chwila t2 – w połowie czasu pomiędzy δT
Rys. 4: Ładowanie i rozładowywanie kondensatora C.
a
T.
A
więc
kondensator
jest
doładowywany przez czas T/2 (i przez taki
sam czas jest rozładowywany). Obliczmy
więc, jaka porcja ładunku zostanie do niego doprowadzona w tym czasie:
Q=I CŚR
T
2
(15)
gdzie ICŚR to średni prąd wpływający do kondensatora w czasie, kiedy jest on doładowywany.
Oglądając uważnie rysunek widzimy, że ten prąd (odpowiadający polu powierzchni pod „trójkątem
prądu” pomiędzy chwilami t1 i t2):
I CŚR =
IL
4
(16)
7
a ΔIL,(12):
I L=
U I −U O
1−
T =U I
T
L
L
(17)
Po podstawieniu (17) do (16) i (16) do (15) otrzymujemy:
Q=
U I 1−
(18)
8Lf 2
gdzie f = 1/T (częstotliwość pracy konwertera).
Teraz w końcu możemy obliczyć amplitudę tętnień Ut:
U t=
Q U I 1−
=
C
8LCf 2
(19)
lub, jeśli wcześniej założyliśmy Ut, potrzebną pojemność kondensatora:
C=
U I 1−
(20)
8U t Lf 2
Tę pojemność należy traktować jako minimalną i zaokrąglić ją co najmniej do najbliższej
„z szeregu” w górę, a najlepiej – o ile to możliwe – zwiększyć znacząco (nawet kilkakrotnie).
Na koniec kilka ważnych uwag:
•
•
•
Amplituda tętnień w konwerterze obniżającym napięcie nie zależy od prądu płynącego do
obciążenia. To ciekawa właściwość, charakterystyczna tylko dla tego typu układu (w konwerterze
podwyższającym napięcie tak nie jest!).
Kształt tętnień (tj. kształt przebiegu napięciowego na kondensatorze) wynika z kształtu prądu, jaki
wpływa i wypływa do/z kondensatora. Jako że jest to prąd na przemian liniowo narastający
i liniowo opadający, przebieg napięcia tętnień jest zbudowany z fragmentów przebiegów
parabolicznych (kondensator jest elementem całkującym wpływający do niego prąd i jeśli ten prąd
liniowo narasta, to napięcie na okładkach kondensatora narasta parabolicznie).
Tętnienia napięcia wyjściowego są niejako wbudowane w układ - ich obecność wynika z samej
zasady jego działania, więc występują zawsze. Aby je wyeliminować, należy zastosować dodatkowe
układy filtrujące, dołączone do wyjścia konwertera.
Przedstawione dotychczas rozważania kończą podstawowy etap projektowania konwertera stepdown, jednak w praktycznej realizacji należy jeszcze dobrać odpowiedni rdzeń cewki, diodę, tranzystor,
oraz zaprojektować obwód sterowania tranzystora.
4. Jak to się projektuje – etap 2
4.1 Dobór rdzenia cewki
Jak zostało powiedziane w rozdziale 3.3, rdzeń cewki dobieramy pod kątem częstotliwości, na jaką
projektujemy konwerter. Musimy tak dobrać rdzeń, by nie pracował on w zakresie częstotliwości, w którym
jego stratność jest znaczna. W tym celu musimy zajrzeć do katalogu.
Jeśli projektujemy cewkę o niewielkich rozmiarach (do konwertera o niewielkiej mocy – do
kilkunastu W) i jednym uzwojeniu, możemy się zdecydować na użycie rdzenia kubkowego. Przy większych
mocach i wielu uzwojeniach chętniej stosuje się rdzenie typu E, EC lub ETD. Jeśli uważnie obejrzymy
rdzeń, jest wielce prawdopodobnym, że odnajdziemy na nim napis „A L = ...”. AL to parametr, który pozwala
w prosty sposób policzyć, ile zwojów musimy nawinąć na rdzeniu dla uzyskania założonej indukcyjności.
Fizycznie AL to indukcyjność jednego zwoju, wyrażona w nH, więc jeśli parametru A L nie znamy, możemy
go – posiadając drut i miernik indukcyjności – łatwo zmierzyć (nawijamy n zwojów na karkas, wsadzamy
do rdzenia, mierzymy indukcyjność L i wyliczamy AL = L[nH] /(n2)).
8
Załóżmy, że chcemy nawinąć cewkę o indukcyjności L. Wówczas liczba potrzebnych zwojów wyraża
się zależnością:
n=
L[nH ]
AL
(21)
Pozostaje jeszcze jedna ważna rzecz, na którą musimy zwrócić uwagę przy dobieraniu rdzenia –
jego rozmiar oraz wielkość szczeliny powietrznej, która z jednej strony zmniejsza przenikalność
magnetyczną, a z drugiej zapobiega zbyt łatwemu nasycaniu się rdzenia. Nie jest to zagadnienie proste,
a działania często opierają się na doświadczeniu lub na pomiarach posiadanego rdzenia.
Więcej na ten temat można znaleźć w dodatku 4.
4.2 Dobór tranzystora i diody
-
Dobierając tranzystor i diodę należy zwrócić uwagę na ich następujące parametry:
dopuszczalna moc maksymalna
maksymalny dopuszczalny prąd średni (kolektora tranzystora, diody)
maksymalny dopuszczalny prąd szczytowy
szybkość działania (przełączania) tych elementów
W impulsowych układach zasilających o niewielkiej mocy wyjściowej problem mocy, jakie się
wydzielają w tranzystorze i diodzie najczęściej nie jest zbyt poważny, jakkolwiek należy pamiętać, że
w miarę wzrostu częstotliwości będzie rosła moc wydzielana w tych elementach w czasie ich przełączania.
Będzie ona tym większa, im czasy włączania/wyłączania zastosowanych kluczy będą dłuższe. Z tego
powodu należy, w miarę możliwości, stosować możliwie szybkie tranzystory i diody, specjalnie
przeznaczone do zastosowań w układach impulsowych. W krańcowym przypadku zastosowanie wolnej
diody „sieciowej” w zasilaczu impulsowym, pracującym z dużą częstotliwością, może doprowadzić do
sytuacji takiej, że nie zdąży się ona w ogóle wyłączyć podczas pojedynczego taktu i będzie się
zachowywała nie jak dioda, a prawie jak kawałek drutu.
Zagadnieniem, na które należy zwrócić większą uwagę, jest wielkość dopuszczalnych prądów –
kolektora tranzystora i diody. Aby określić wymagania wobec diody i tranzystora należy obliczyć zarówno
największy średni prąd, jaki będzie płynął przez każdy z tych elementów, jak i jego maksymalną wartość
szczytową.
a. prądy średnie
- tranzystor: w czasie taktu wejściowego tranzystor jest włączony w szereg z cewką i obciążeniem
konwertera, więc średni prąd jego kolektora w czasie pomiędzy chwilą 0 a δT jest równy I O i jest
oczywiście największy dla IO = IOMAX. Maksymalny prąd kolektora tranzystora, uśredniony w całym okresie
T, jest równy:
I CAVmax=I OMAX
T
= I OMAX
T
(22)
- dioda: analogicznie do sytuacji w punkcie poprzednim, IOMAX jest maksymalną wartością średniego prądu
diody w czasie taktu wyjściowego, czyli od chwili δT do T. Po uśrednieniu tego prądu za cały ukres
otrzymujemy zależność:
I DAVmax =I OMAX
T − T
=1− I OMAX
T
(23)
Z powyższych zależności wypływa ważny wniosek: im mniejszy jest współczynnik δ, tym większy
jest stosunek średniego prądu płynącego przez diodę do średniego prądu płynącego przez tranzystor.
Inaczej mówiąc: im większe jest „przełożenie” napięcia wejściowego na wyjściowe, tym „mocniejsza” musi
być dioda i tym „słabszy” może być tranzystor.
9
b. prądy maksymalne (szczytowe, chwilowe)
Maksymalne prądy szczytowe płyną przez oba elementy w chwili δT, w sytuacji kiedy IO = IOMAX. Dla
obu elementów – diody i tranzystora – prądy te są jednakowe.
Patrząc na rysunek 2 nietrudno zauważyć, że:
1
I CMAX =I DMAX =I OMAX I L
2
(24)
Korzystając z równań (2) i (5) otrzymujemy:
I CMAX =I DMAX =I OMAX U I
1−
2fL
(25)
4.3 Obwód sterowania tranzystora
Widoczny na rys. 1b tranzystor to tranzystor PNP z emiterem dołączonym do napięcia wejściowego
UI. Z włączeniem tak podłączonego tranzystora problemu nie ma – wystarczy, przy pomocy niskiego
potencjału (może to być nawet masa) i opornika w bazie, wywołać prąd bazy I B. Jeśli ten prąd będzie
spełniał zależność:
I B
IC
(26)
gdzie β – wzmocnienie prądowe tranzystora, tranzystor się nasyci i „podłączy” napięcie U I do lewej
końcówki cewki.
Niestety sytuacja jest dużo gorsza, gdy chcemy tranzystor wyłączyć, bo wtedy musimy na jego
bazę podać napięcie UI (lub wyższe). To na ogół jest bardzo niewygodne, bowiem wymaga zbudowania
generatora „przyklejonego” do napięcia zasilającego.
Należy więc obwód sterowania bazy tranzystora zmodyfikować tak, by mógł on być sterowany na
przykład z typowego układu logicznego, w którym U L (napięcie stanu niskiego) to około 0 V, a U H (napięcie
stanu wysokiego) jest dodatnie i wynosi kilka woltów.
Przykład praktycznego rozwiązania, dostosowującego
typowy układ logiczny do tranzystora naszego konwertera
pokazuje rys. 5. Tranzystor Q1 to klucz nasycony, którego
kolektor steruje bezpośrednio prądem bazy tranzystora Q. Jeśli
tranzystor Q1 jest wyłączony – prąd bazy tranzystora Q jest
równy 0 i tranzystor Q też jest wyłączony. Natomiast jeśli prąd
kolektora tranzystora Q1 płynie, powoduje on przepływ prądu
bazy tranzystora Q i w rezultacie jego włączenie (powinno dojść
do nasycenia tranzystora Q). Projektowanie układu sterowania
tranzystora Q polega na takim dobraniu wszystkich rezystorów,
by oba tranzystory pracowały jako klucze, czyli wyłącznie
w stanach nasycenie – zatkanie.
Zacznijmy od obliczenia, jaki musi być prąd bazy
Rys. 5: Przykład układu sterowania
tranzystora Q, by – w czasie kiedy ma pracować jako włączony
tranzystora kluczującego Q.
klucz – na pewno pozostał w nasyceniu. Z równania (25) wiemy,
jaki największy prąd może płynąć przez kolektor tranzystora Q.
Aby ten tranzystor był nasycony, nawet przy tym prądzie musi
być spełniona zależność (26), i to dla najmniejszej możliwej β. A w praktyce, by nasycenie tranzystora Q
było pewne, prąd bazy IB powinien być jeszcze co najmniej 2 - 5 razy większy. Możemy więc napisać:
I BQ=2...5
1
MIN
I OMAXU I
1−
2f L
(27)
10
Zadaniem rezystora RE (kilkaset Ω – kilka kΩ) jest przyspieszenie procesu wyłączania tranzystora
Q, natomiast w czasie włączenia tego tranzystora płynie przezeń prąd:
I R E=
U BEPQ 0,7 V
=
RE
RE
(28)
Jako że tranzystor Q1 ma pracować jako klucz, wywoła on prąd bazy tranzystora Q wtedy, kiedy
będzie w stanie nasycenia. Wówczas napięcie na jego kolektorze będzie równe około 0,2 V, a więc
pomijalnie małe wobec napięcia na bazie włączonego (nasyconego) tranzystora Q (to napięcie jest równe
UI – UBEPQ). Można więc, uwzględniając (27) i (28), obliczyć potrzebną wartość rezystancji R C:
RC =
U RC U I −0,7 V
=
I RC
I BQI R E
(29)
Rezystor RB dobieramy tak, by podane z logicznego układu sterującego napięcie U H powodowało
jego pewne nasycenie:
RB =
U H −U BEPQ1
2...5⋅I RC / MINQ1
(30)
Oczywiście, jeśli napięcie niskie stanu logicznego UL < 0,7 V, po jego podaniu na wejście tranzystor
Q1 będzie wyłączony, co spowoduje też wyłączenie tranzystora Q.
5. Z 20 na 5 V, czyli przykład projektowania konwertera
Wróćmy do przykładu z pierwszego rozdziału: należy zaprojektować konwerter impulsowy, który
umożliwi uzyskanie napięcia wyjściowego UO = 5 V przy maksymalnym prądzie obciążenia I OMAX = 1 A.
Napięcie wejściowe, jakim dysponujemy, to UI = 20 V.
Brakuje nam jeszcze jednej danej: minimalnego prądu I OMIN, jakim będziemy obciążali nasz
konwerter (przy obciążeniu mniejszym niż ten prąd napięcie na wyjściu konwertera będzie większe od 5 V,
dążąc – dla zupełnego braku obciążenia – do 20 V).
Zwiększanie się napięcia na wyjściu przy niedociążeniu jest poważną wadą impulsowych
konwerterów napięcia i w praktyce są w nich stosowane różnego rodzaju zabezpieczenia przed taką
sytuacją. Najprostszym (ale i nienajlepszym) sposobem zabezpieczenia jest zastosowanie wstępnego
obciążenia, w postaci opornika dołączonego pomiędzy wyjście a masę. Zastosowanie takiego opornika
oznacza oczywiście powstanie stałych strat mocy i obniża sprawność konwertera (tym bardziej, im
mniejszą moc pobieramy z jego wyjścia), jednak ze względu na ogromną prostotę to rozwiązanie
w układach o niewielkiej mocy bywa stosowane. Zastosujmy je więc w naszym przykładzie. Inne pomysły
na zabezpieczenie konwertera przed niedociążeniem można znaleźć w dodatku 5.
5.1 Dobieramy opornik wstępnie obciążający konwerter
Przypomnijmy: gdybyśmy chcieli uzyskać założone napięcie wyjściowe w układzie liniowym,
sprawność tego układu nie przekroczyłaby 25%. Załóżmy wstępnie (potem to założenie zweryfikujemy),
że układ impulsowego przetwarzania napięcia przy maksymalnym prądzie wyjściowym będzie miał
sprawność nie mniejszą, niż 80%. Jeśli więc „dorzucimy” kolejnych 5% strat w oporniku R OBC, i tak
sprawność układu impulsowego będzie i tak około trzy razy większa niż liniowego. Policzmy więc.
Założona moc strat w oporniku:
POBC =0,05⋅5W =0,25 W
stąd:
ROBC =
U 2O
5V 2
=
=100
POBC 0,25 W
11
Mamy więc już wartość minimalnego prądu (czyli prądu krytycznego), jaki będzie pobierany
z konwertera:
I OMIN =I OKR =
5V
=50 mA
100
Należy podkreślić, że dobieranie opornika obciążającego jest najczęściej bardzo zgrubne, a kryteria
jego doboru są umowne. Może się zdarzyć tak, że „punktem wyjścia” nie będą dopuszczalne dodatkowe
straty, a wprost minimalny prąd pobierany z konwertera. W każdym przypadku należy się kierować
narzuconymi danymi projektowymi, indywidualnymi oszacowaniami, oraz tym na jakie stałe straty można
sobie w konkretnym układzie pozwolić. Przypomnijmy, że nie trzeba w ogóle dodawać tego opornika, jeśli
obciążenie pobierające prąd większy od krytycznego jest dołączone do wyjścia konwertera na stałe.
5.2 Obliczanie współczynnika wypełnienia oraz dobór częstotliwości pracy
Korzystając z (5) otrzymujemy:
5V
=0,25
20 V
=
Jest to wartość obliczona przy pominięciu spadków napięć na nasyconym tranzystorze
i przewodzącej diodzie. Jednak przy małym napięciu wyjściowym i sporym prądzie I O może być pożądane
uwzględnienie spadku napięcia na przewodzącej diodzie, (zwłaszcza w przypadku, gdy zostanie
zastosowana dioda typu P-N o znacznym napięciu przewodzenia) oraz napięcie nasycenia tranzystora dla
większych prądów IC. Korzystając z (5a) z dodatku 2 i zakładając wstępnie, że U CES = 0,5 V oraz UF = 1 V
otrzymujemy:
5 V 1 V
=0,292
20 V 1 V −0,5 V
=
Jak widać, zmiana w stosunku do poprzedniej wartości to prawie 20%, a więc znacząca.
W praktyce może się okazać jeszcze większa, bo przy sporych prądach napięcie przewodzenia diody P-N
może sięgać nawet 1,5 V i więcej. Zastosowanie w naszym układzie diody Schottky'ego poprawiłoby
sytuację w stopniu znaczącym.
Na tym etapie projektowania trzeba jeszcze wybrać częstotliwość pracy konwertera. Wstępnie
załóżmy, że będzie to np. 25 kHz (okres T = 40 μs). Tak możemy postąpić wtedy, kiedy nie mamy
narzuconego typu ferrytu, z którego będzie wykonany rdzeń cewki. Jeśli jest inaczej, najpierw
sprawdzamy własności posiadanego materiału ferrytowego, a następnie wybieramy częstotliwość. O ile
jest to możliwe, powinna ona być większa od około 20 kHz, lecz niższa od tej, dla której stratność użytego
ferrytu zaczyna gwałtownie rosnąć.
5.3 Obliczanie indukcyjności cewki i dobór jej rdzenia
Do obliczenia indukcyjności cewki potrzebny nam jest prąd I OMIN. Z rozważań wcześniejszych
wynika, że w projektowanym konwerterze wynosi on 50 mA. To będzie prąd krytyczny I OKR naszego
konwertera.
W rozdziale 3.3 odnajdujemy zależność (13) i po podstawieniu stosownych wartości otrzymujemy:
L=
20 V⋅0,292⋅1−0,292
=1,65 mH
2⋅25 kHz⋅50 mA
Możemy teraz spróbować dobrać rdzeń cewki i obliczyć liczbę zwojów, które będziemy musieli
nawinąć dla uzyskania pożądanej indukcyjności.
Zaglądając do dodatku 3 możemy się zorientować, że odpowiednim materiałem na rdzeń naszej
cewki może być na przykład ferryt typu F1501 lub F2002. Zakładając, że posiadamy np. rdzeń kubkowy o
AL = 320, do równania (21) podstawiamy dane i obliczamy:
n=
1650000 nH
=71,8
320nH
12
Oczywiście nawinięcie ułamkowej części zwoju jest niemożliwe, więc zaokrąglamy liczbę zwojów
w górę – do 72. W praktyce możemy nawinąć o kilka zwojów więcej, bowiem zwiększanie indukcyjności
skutkuje zmniejszaniem IOKR i w ten sposób uzyskamy pewien zapas. Ze zwiększaniem liczby zwojów
należy jednak uważać, bo ich nadmierna liczba może być przyczyną powstania dodatkowych strat lub
nasycania się rdzenia cewki.
5.4 Dobór kondensatora
Kondensator dobieramy, korzystając z zależności (20) z rozdziału 3.4 i zakładając dopuszczalne
napięcie tętnień Ut. Załóżmy, że nie chcemy, aby amplituda tętnień napięcia wyjściowego naszego
konwertera przekroczyła 5 mV.
Obliczamy:
C=
20 V⋅1−0,292⋅0,292
=100,23 uF
8⋅5 mV⋅1,65 mH⋅25 kHz 2
Jeżeli chcemy mieć stuprocentową pewność, że tętnienia nie przekroczą założonej wartości,
zastosujemy kondensator „z zapasem”, o pojemności 220 μF, a jeżeli bardzo nam zależy na oszczędności
miejsca i możemy się zgodzić na ryzyko pojawienia się nieco większych tętnień – 100μF. Pamiętajmy
jednak, że kondensatory elektrolityczne (a taki trzeba będzie tu zastosować) są bardzo niedokładne
i typowy rozrzut wartości ich pojemności to -20...+50%. Co więcej, tego typu kondensatory potrafią tracić
część swojej pierwotnej pojemności wraz z upływem czasu.
Wyliczona wartość pojemności C jest, jak na konwerter impulsowy o niewielkiej mocy, spora – ale
akceptowalna. Należy jednak pamiętać o jeszcze jednej ważnej rzeczy. Kondensatory elektrolityczne wraz
ze wzrostem częstotliwości częściowo tracą swoje właściwości (bo posiadają stosunkowo dużą szeregową
indukcyjność), więc równolegle z takim kondensatorem należy koniecznie wlutować drugi –
nieelektrolityczny (najlepiej ceramiczny), o pojemności rzędu kilkadziesiąt - kilkaset nanofaradów.
5.5 Wybieramy tranzystor i diodę
Aby dobrać tranzystor i diodę, musimy określić wymagania wobec ich dopuszczalnych prądów:
- maksymalne prądy średnie. Korzystamy z równań (22) i (23) oraz uwzględniamy prąd wstępnego
obciążenia konwertera (50 mA):
I CAVmax=0,292⋅1,05 A=306 mA czyli ok. 300 mA
I DAVmax =1−0,292⋅1,05 A=743 mA ok. 800 mA
- prądy maksymalne chwilowe. Z (25) otrzymujemy:
I CMAX =I DMAX =1,05 A20 V
0,292⋅1−0,292
=1,1 A
2⋅25 kHz⋅1,65 mH
Należy też zwrócić uwagę na maksymalne napięcia, jakie się mogą pojawić na tranzystorze i na
wyłączonej diodzie. W obu przypadkach jest to około 20 V. Musimy więc wybrać z katalogu elementy
o następujących parametrach:
- tranzystor:
IC > 300 mA
ICM > 1,1 A
UCEMAX > 20 V
(dopuszczalny prąd średni)
(dopuszczalny prąd szczytowy)
(dopuszczalne napięcie kolektor – emiter)
-dioda:
IFAV > 800 mA
IFRM > 1,1 A
VRRM > 20 V
(dopuszczalny prąd średni)
(dopuszczalny prąd szczytowy)
(napięcie przebicia wstecznego)
Oczywiście należy wybrać elementy z pewnym zapasem i zwrócić uwagę na ich własności przy
przełączaniu (dla obu elementów będzie to czas wyłączania).
13
Przykładowe elementy o wymaganych parametrach to:
- tranzystor:
BC 313 (IC = 1 A, UCEMAX = 40 V, tOFFMAX = 850 ns, UCESAT = 1 V dla IC = 1 A, β > 40)
Zaproponowany tranzystor ma większe od założonego napięcie nasycenia, więc teoretycznie –
chcąc być bardzo dokładnym – należałoby skorygować wcześniejsze obliczenia. Jednak po ponownym
obliczeniu współczynnika δ okazuje się, że jego zmiana jest mniejsza niż 2,5%, można więc nie zawracać
sobie nią głowy.
Niezłym rozwiązaniem byłoby też zastosowanie tranzystora BD136, którego parametry się
następujące: IC = 1,5 A, UCEMAX = 40 V, PTOT = 12,5 W)
- dioda:
BA 157 (IFAV = 1 A, VRRM = 400 V, IFRM = 10 A, tRRMAX = 300 ns, UF = 1,5 V przy IF = 1 A)
Jako że napięcie wyjściowe naszego konwertera jest niewielkie, korzystniejsze byłoby użycie diody
Schottky'ego, której napięcie przewodzenia to około 0,2 – 0,3 V (zwłaszcza że napięcie przewodzenia
diody BA157 przy prądzie 1 A to aż 1,5 V!).
5.6 Obwód sterowania tranzystora kluczującego
Załóżmy, że nasz konwerter będzie sterowany z generatora impulsów prostokątnych o poziomach:
UL = 0 V
UH = 3 V
Z danych katalogowych odczytujemy, że wzmocnienie prądowe β tranzystora BC313 jest nie
mniejsze niż 40. Możemy więc obliczyć minimalny prąd, jaki należy dostarczyć do bazy tego tranzystora,
by był on pewnie nasycony dla każdego występującego w układzie prądu IC. Z (27):
I BQ=2...5
0,292⋅1−0,292
1
⋅1,05 A20 V
=55...137 ,5 mA
40
2⋅25 kHz⋅1,65 mH
To spory prąd, wynika on z niewielkiej wartości β min użytego tranzystora. W takiej sytuacji czasami
warto narzucić użycie tranzystora z określonej grupy selekcyjnej. W naszym przypadku, gdyby został
użyty tranzystor BC313C, jego najmniejsze wzmocnienie prądowe wynosiłoby 100. Dla takiego tranzystora
prąd IBQ potrzebny do nasycenia byłby dwa i pół raza mniejszy niż przed chwilą obliczony. Załóżmy jednak,
że zostanie zastosowany tranzystor wybrany losowo i sprawmy, by prąd jego bazy wynosił około 80 mA.
Korzystając z (29) dobieramy rezystor RC (rys. 5):
RC =
20 V −0,7V
=240
80 mA
W obliczeniach nie został uwzględniony prąd płynący przez (jeszcze nieznany) opornik R E, ale
zauważmy, że w naszym przypadku znaczenie tego prądu będzie bardzo niewielkie. Jeśli nawet wstawimy
niewielki opór (na przykład RE = 680 Ω), to prąd przezeń płynący będzie równy zaledwie 1 mA.
W porównaniu do 80 mA jest to wartość pomijalna.
Na koniec obliczymy rezystancję RB, ale w tym celu najpierw musimy wybrać tranzystor Q1. Jako że
nie musi być to tranzystor o dużej dopuszczalnej mocy strat, możemy się zdecydować na popularny
(i bardzo tani) tranzystor „typu BC107”, na przykład BC548. Jego wzmocnienie prądowe β to nie mniej niż
200, więc:
RB =
1 3V −0,7 V
=1,15 ...2,7 k
2...5 80 mA / 200
14
Ostatecznie można zaproponować następujące wartości rezystancji oporników:
RB = 1,5 kΩ
RC = 220 Ω
RE = 680 Ω
będąc świadomym, że są to wartości orientacyjne, wybranie z obliczonych przedziałów w sposób dosyć
swobodny (na przykład zastosowano opornik o rezystancji 220 Ω zamiast 240 Ω, bo doświadczenie uczy,
że jest on dużo łatwiej „zdobywalny”). Na szczęście w układach zbudowanych z nasyconych kluczy wielka
precyzja nie jest potrzebna, należy jedynie dbać o pewne (ale nie przesadnie głębokie!) nasycanie się
tranzystorów.
5.7 Na zakończenie – jaka jest sprawność zaprojektowanego układu?
Sprawność naszego konwertera to stosunek mocy, jaką pobieramy z jego wyjścia, do mocy, jaką
konwerter pobiera ze źródła napięcia U I. Jako że zostało zastosowane zabezpieczenie przed wzrostem
napięcia wyjściowego w postaci dociążenia konwertera stałym prądem (50 mA), niezależnym od aktualnej
wartości prądu IO, sprawność całego układu jest zależna od obciążenia i jest największa dla I O = IOMAX.
W takiej sytuacji moc pobierana z wyjścia konwertera to:
PO=U O I OMAX50 mA =5V⋅1,05 A=5,25 W
a moc pobierana z napięcia UI:
PI =U I I CAVmax =20 V⋅306 mA =6,12W
A więc maksymalna sprawność zaprojektowanego konwertera to:
MAX=
PO
=0,857
PI
W rzeczywistości sprawność będzie nieco mniejsza, bowiem wystąpią dodatkowe straty wynikające
z rezystancji drutu cewki, stratności zastosowanego ferrytu i skończonej szybkości przełączania
tranzystora oraz diody. Jednak jeśli nawet całkowita sprawność konwertera spadnie o kolejnych 10% (do
około 0,75) i tak widać wyraźnie, że sprawność konwertera impulsowego przy pełnym obciążeniu jest
około trzykrotnie większa, niż odpowiadającego mu układu liniowego.
15
Dodatek 1 – cewka a kondensator (autor: A. Burd)
Kondensator:
• Nie można skokowo zmienić napięcia na kondensatorze (bo wymagałoby to „nieskończonego
prądu”).
• Dla skoku kondensator zachowuje się jak „zwarcie” (dokładniej od „bateria” o napięciu między
okładkami takim, jakie było tuż przed skokiem).
• Ładowanie kondensatora stałym prądem: jeśli do kondensatora wpływa stały prąd, to napięcie na
kondensatorze rośnie liniowo.
• Im większy jest prąd ładowania i im mniejsza pojemność, tym szybciej napięcie na kondensatorze
narasta.
• Z naładowanego uprzednio kondensatora (tj. kondensatora, w którym zgromadził się określony
ładunek elektryczny) można czerpać energię trochę tak jak z baterii, ale oczywiście ładunek będzie
się zmniejszał (czyli napięcie na kondensatorze będzie się tak samo zmniejszać) wraz z odpływem
tej energii.
• Powiązanie pojemności C, prądu ładującego IC oraz zmiany napięcia ΔUC w czasie ΔT (ładowanie
kondensatora stałym prądem) opisuje wzór:
T=
C⋅ U C
IC
Cewka:
• Nie można skokowo zmienić prądu w cewce (chyba że dysponuje się „nieskończonym napięciem”).
• Dla skoku cewka zachowuje się jak „rozwarcie” (dokładnie jak źródło prądowe o wydajności równej
wartości prądu, jaki płynął tuż przed skokiem).
• „Ładowanie” cewki stałym napięciem: jeśli do cewki zostanie przyłożone napięcie (różnica
potencjałów), to prąd w cewce będzie narastać liniowo;
• im większe jest napięcie przyłożone do cewki i im mniejsza indukcyjność, tym szybciej prąd
w cewce narasta.
• Z „naładowanej” uprzednio cewki (tj. cewki, w której wcześniej wymuszono przepływ prądu
i wywołano strumień magnetyczny) można czerpać energię, przy czym cewka zachowuje się jak
źródło prądowe, ale oczywiście strumień będzie malał (i prąd cewki będzie też malał) wraz
z odpływem tej energii.
• Powiązanie indukcyjności L, przyłożonego do cewki napięcia U L i zmian prądu ΔIL w czasie ΔT
opisuje wzór:
T=
L⋅ I L
UL
16
Dodatek 2 – dla aptekarzy: uwzględnianie UF i UCES
W przypadku, gdy chcemy uwzględnić spadki napięć na włączonych kluczach (nasyconym
tranzystorze i przewodzącej diodzie), musimy zmodyfikować równania (2) i (3).
Pierwsze z nich opisuje zmianę prądu w cewce w takcie wejściowym, w którym nasycony tranzystor
jest włączony w szereg z cewką. Powoduje to zmniejszenie przyłożonego do niej napięcia o napięcie
nasycenia tranzystora UCES. Otrzymujemy więc zmodyfikowane równanie:
I L=
U I −U O−U CES
T
L
(2a)
W równaniu (3) należy uwzględnić spadek napięcia U F na przewodzącej diodzie, zwiększający
napięcie przyłożone do cewki w czasie trwania taktu wyjściowego (anoda diody jest dołączona do masy,
więc potencjał jej katody staje się ujemny):
− I L=
−U O−U F
T − T
L
(3a)
Ostatecznie możemy zapisać:
U I −U O−U CES
U U F
T= O
T−T
L
L
(4a)
z czego otrzymujemy aptekarską zależność:
=
U O U F
U I U F −U CES
(5a)
17
Dodatek 3 – przykładowe charakterystyki rdzeni ferrytowych (materiały POLFER)
18
19
20
Dodatek 4 – nasycanie się rdzenia cewki
Nasycanie się ferrytowego rdzenia cewki to jedno z poważniejszych niebezpieczeństw, na jakie
może się natknąć konstruktor zasilacza impulsowego. Zjawisko to może doprowadzić do
niekontrolowanego wzrostu prądu klucza (prądu kolektora lub drenu tranzystora) i do jego
natychmiastowego zniszczenia.
W dotychczasowych rozważaniach zakładaliśmy, że indukcyjność cewki zależy tylko od parametru
AL zastosowanego rdzenia i liczby nawiniętych zwojów. W rzeczywistości indukcyjność cewki z rdzeniem
ferrytowym zależy też od kilku innych czynników, w tym od natężenia pola magnetycznego w cewce.
Zacznijmy od podstawowych fizycznych zależności:
1. Natężenie pola magnetycznego H w cewce bez rdzenia:
H=
n⋅I L
l
(4-1)
gdzie: n - liczba zwojów, IL - natężenie prądu w cewce, l - długość cewki
Dla nas najważniejsze jest to, że natężenie pola jest wprost proporcjonalne do prądu płynącego
w cewce do i liczby zwojów.
2. Indukcja magnetyczna B w cewce z rdzeniem:
B= 0⋅ r⋅H
(4-2)
μ0 - przenikalność magnetyczna próżni (wielkość stała),
μr - przenikalność magnetyczna względna (wielkość zależna od materiału, z którego jest wykonany rdzeń).
Dla rdzeni ferrytowych μr » 1 (może sięgać nawet kilku - kilkunastu tysięcy).
Niestety w przypadku materiałów ferromagnetycznych μr nie jest wielkością stałą, a zależy od H.
Orientacyjny wykres tej zależności, oraz zależności B od H (jest to tzw. krzywa magnesowania),
przedstawia poniższy rysunek:
Widać, że dla małych natężeń pola magnetycznego przenikalność względna wraz ze wzrostem H
nawet nieco rośnie, natomiast po osiągnięciu pewnej wartości maksymalnej zaczyna gwałtownie spadać
(dla bardzo dużych wartości H, μr zbliża się do jedności). W przypadku wywołania w cewce bardzo dużego
natężenia pola magnetycznego cewka z rdzeniem zachowywałaby się tak, jak cewka powietrzna (bez
rdzenia).
3. Indukcyjność jednowarstwowej cewki z rdzeniem:
L=
0⋅ r⋅S 2
⋅n
l
(4-3)
gdzie S - pole powierzchni przekroju cewki, l - długość cewki, n - liczba zwojów.
21
W przypadku cewki wielowarstwowej zależność jest nieco bardziej skomplikowana, ale i w tym
przypadku indukcyjność jest tym większa, im większa jest liczba zwojów, a także tym większa, im większa
jest względna przenikalność magnetyczna zastosowanego rdzenia (najmniejsza jest zawsze dla cewki
powietrznej).
Zestawmy teraz na wszystkie przedstawione wyżej zależności oraz zjawiska i zastanówmy się, jakie
to może mieć konsekwencje dla działania impulsowego konwertera napięcia.
Aby uzyskać zaprojektowaną indukcyjność na konkretnym rdzeniu, musimy nawinąć na nim
określoną liczbę zwojów n (zazwyczaj obliczamy ją korzystając z parametru A L). Przez tę cewkę będzie
przepływał prąd IL, narastający liniowo aż do pewnej wartości maksymalnej ILK (ILK jest tym większe, im
większy jest prąd IO, pobierany z wyjścia konwertera). Z zależności (4-1) wynika, że w miarę wzrostu
prądu cewki będzie rosło natężenia pola magnetycznego H, osiągając wartość największą dla prądu ILK.
Jeśli natężenie pola wzrośnie do takiej wartości, że przenikalność μr przekroczy swoje maksimum i zacznie
się zmniejszać (patrz rysunek), będzie to miało wpływ na indukcyjność cewki zgodnie z zależnością (4-3).
Wartość indukcyjności L zacznie spadać, i to tym bardziej, im większy prąd będzie płynął przez cewkę.
Przypomnijmy sobie teraz jeszcze raz podstawową zależność, wiążącą prąd w cewce z przyłożonym
do niej napięciem:
i L t=I L0
UL
⋅t
L
(4-4)
A więc: im mniejsza jest indukcyjność cewki, tym szybciej (przy tym samym napięciu do niej
przyłożonym) narasta w tej cewce prąd. Jeśli prąd stanie się tak duży, że (zgodnie z tym, co napisano
wyżej) zacznie to powodować zmniejszanie się indukcyjności cewki, prąd zacznie narastać jeszcze
szybciej. Z kolei coraz szybszy wzrost prądu powoduje coraz silniejsze zmniejszanie się indukcyjności, co
powoduje wzrost prądu, co powoduje spadek indukcyjności.... i koło się zamyka - po przekroczeniu
pewnej wartości prądu zjawisko „napędza się samo” i niewiele trzeba, by chwilowy prąd IL stał się dużo
większy od największego zakładanego. A ponieważ prąd cewki płynie na przemian przez tranzystor i przez
diodę, jeden z tych elementów może ulec zniszczeniu.
Na rysunku poniżej pokazano przebieg prądu w cewce konwertera po przekroczeniu takiego prądu
obciążenia IO, który powoduje wchodzenie rdzenia cewki w stan nasycenia.
22
Dodatek 5 - alternatywne zabezpieczanie konwertera przed niedociążeniem
Zabezpieczenie konwertera przed niedociążeniem przez jego wstępne dociążenie to działanie
skuteczne, ale też najprostsze i najmniej ekonomiczne (bo powoduje znaczący spadek sprawności
konwertera).
Innym zabiegiem może być dołączenie do wyjścia konwertera elementu nieliniowego, który zaczyna
być widoczny jako wstępne obciążenie dopiero wtedy, kiedy zaistnieje taka potrzeba (czyli wyłącznie
w sytuacji, gdy konwerter jest rzeczywiście zbyt słabo obciążony).
Żeby dłużej nie owijać w bawełnę, powiedzmy wprost: taki elementem jest zwykła dioda Zenera...
Reasumując: jeśli do wyjścia impulsowego konwertera napięcia dołączymy równolegle (a więc
pomiędzy jego wyjście a masę) diodę Zenera o napięciu przebicia ciut większym od nominalnego napięcia
wyjściowego (czyli napięcia w sytuacji, gdy konwerter jest obciążony prądem Io > IOKR), ta dioda Zenera
w stanie „normalnej” pracy nie jest nijak widoczna (bo nie przewodzi). Jednak gdy prąd obciążenia
konwertera spadnie poniżej IOKR i niedociążony konwerter „chciałby” zwiększyć napięcie na swoim wyjściu,
dioda Zenera ulegnie przebiciu i popłynie przez nią prąd zbliżony do I OKR. W ten sposób dioda zapewni
dociążenie układu w sytuacji, gdy prąd pobierany z jego wyjścia byłby zbyt mały, by zapewnić spełnienie
zależności (5).
Jednak, stosując diodę Zenera jako zabezpieczenie przed niedociążeniem należy mieć na uwadze
kilka ważnych rzeczy:
1. Dopuszczalna moc strat diody.
Jeśli napięcie wyjściowe konwertera jest wysokie, a zakładany prąd I OKR jest spory, należy się
uważnie przyjrzeć mocy, jaka będzie rozpraszana w diodzie Zenera w sytuacji, kiedy zostanie ona
włączona.
Na przykład: jeśli zaprojektowaliśmy konwerter na napięcie wyjściowe 30 V, a prąd włączenia diody
(czyli IOKR) to 100 mA, moc wydzielona w diodzie po niedociążeniu układu to mniej więcej 3W (!), czyli delikatnie mówiąc - sporo.
2. Napięcie włączenia (przebicia) diody a napięcie wyjściowe konwertera.
Problem może się pojawić głównie wtedy, kiedy konwerter jest projektowany na niewielkie napięcie
wyjściowe.
Dioda Zenera powinna mieć napięcie przebicia wyraźnie wyższe, niż nominalne napięcie wyjściowe
(jeśli dioda włączy się w zakresie pracy nadkrytycznej konwertera, ulegnie natychmiastowemu
zniszczeniu) a do tego należy jeszcze dodać tolerancję napięcia znamionowego zastosowanej diody.
Przykład: jeśli projektujemy konwerter na napięcie wyjściowe 5 V, zastosowanie diody Zenera
o katalogowym napięciu przebicia równym 5,1 V uznałbym za ryzykowne.
Przy tolerancji UZ równym 5% rzeczywiste napięcie przebicia diody może się wahać od około 4,8 V
do około 5,3 V. Jeśli więc „trafi się” dioda o pechowym napięciu UZ = 4,8V, prawdopodobnie ulegnie ona
(przy normalnej pracy konwertera) natychmiastowemu zniszczeniu. Stąd wniosek, że bezpiecznym byłoby
zastosowanie diody zabezpieczającej nie o napięciu 5,1 V, a o napięciu 5,6 V („na styk”) lub (znacznie
bezpieczniej) nawet 6,2 V (to kolejne napięcia wzięte z, typowego dla diod Zenera, szeregu E24).
Jednak w najgorszym przypadku: 5,2 V + 5% to prawie 5,5 V, a 6,2 V + 5% to 6,5 V! Jeśli więc
trafi nam się dioda z najwyższą odchyłką „w górę” to może się okazać, że zanim się włączy
zabezpieczenie, napięcie wyjściowe przekroczy napięcie nominalne o 10 - 30% (!).
To dużo i niekoniecznie każdy układ, zasilany z projektowanego konwertera, będzie na takie
przekroczenie napięcia zasilania odporny.
23