(rekonstrukcja).

Fizyka, technologia oraz modelowanie wzrostu
kryształów
Stanisław Krukowski i Michał Leszczyński
Instytut Wysokich Ciśnień PAN
01-142 Warszawa, ul Sokołowska 29/37
tel: 88 80 244
e-mail: [email protected], [email protected]
Zbigniew Żytkiewicz
Instytut Fizyki PAN
02-668 Warszawa, Al. Lotników 32/46
E-mail: [email protected]
Wykład – 2 godz./tydzień – czwartek 8.15 – 10.00
Interdyscyplinarne Centrum Modelowania UW
Budynek Wydziału Geologii UW – sala 3089
http://www.icm.edu.pl/web/guest/edukacja/fizkruk0809
http://www.unipress.waw.pl/~stach/wyklad_ptwk_2008
Wykład 3. Równowagowe własności powierzchni
krystalicznych
Fazy skondensowane (stała, ciekła) – ujemna entalpia układu
Energia oddziaływania – np.
potencjał Lennarda-Jonesa (gazy
szlachetne)
1.00
0.75
0.50
0.25
6
0.00
V/ε
 r 
r 
E(r ) = ε   −   
 σ  
 σ 
12
-0.25
-0.50
-0.75
-1.00
0.8
1.0
1.2
1.4
1.6
1.8
2.0
2.2
r/σ
Do entalpii układu (jego energii wiązania) daje wkład wiele warstw
atomowych.
2.4
2.6
2.8
3.0
Własności energetyczne warstw powierzchniowych
Gęstość oraz energia oddziaływania – zmienia się w sposób ciągły
Energia
Gęstość
Grubość warstwy powierzchniowej
może być bardzo różna, jednak w
wielu przypadkach, np. kryształy
półprzewodników lub kryształy
jonowe, może to być wiele warstw
atomowych.
Stosuje się wiele różnych przybliżeń
do opisu własności powierzchni,
jednak najprostszym jest opis Gibbsa
Model powierzchni Gibbsa
• Model Gibbsa – jednorodne własności faz objętościowych i
dodatkowa gęstość (masy, energii, itp.) przypisywana powierzchni
– gdy zachodzi taka potrzeba
Energia
Można wybrać położenie
powierzchni tak, aby znikała
powierzchniowa gęstość masy lub
powierzchniowa gęstość energii.
Gęstość
W przypadku układy zawierającego
kilka składników można wybrać
położenie tak aby znikała
powierzchniowa gęstość jednego ze
składników.
Opis standardowy – znika powierzchniowa gęstość masy
Energia swobodna kryształu F jest sumą wkładu objętościowego i
powierzchniowego:
r
r
F = ∫ f s (T, p, r ) dV + ∫ f l (T, p, r ) dV + ∫ γ (θ, ϕ, T, p) dS
Vs
Vl
S
µl,s - potencjał chemiczny (s,l)
fl,s - gęstość energii swobodnej na jednostkę objętości faz (s,l)
γ - gęstość energii powierzchniowej
Energia swobodna – w modelu Gibbsa jest więc równa:
F = f s (T, p)Vs + f l (T, p)Vl + γ (θ, ϕ, T, p)A
Napięcie powierzchniowe - i powierzchniowa gęstość energii
•
Powierzchniowa gęstość energii
F=
∫ γ(θ, T, p) dS = γ(θ, T, p)A
A
•
Napięcie powierzchniowe – siła działające na jednostkę długości obwodu
powierzchni
r
σ
Praca potrzebna na zwiększenie obwodu = zmiana energii powierzchni
r r r
r
W = ∫ dlσ * δx ≅ σ δA = σ
∆Fpow = γδA
r
σ =γ
Zwilżanie powierzchni
•
Rozważmy 3 układy: faza stała(1), faza gazowa(3) oraz inna faza (ciekła
lub stała - 2)
•
Własności energetyczne powierzchni są określone przez ich energie
powierzchniowe (napięcia powierzchniowe):γγ12, γ13, γ23.
(A)
•
(B)
Całkowite zwilżanie powierzchni (A) zachodzi gdy
γ13 > γ12 + γ 23
Częściowe zwilżanie powierzchni – kąt zwilżania
•
Częściowe zwilżanie powierzchni (A) zachodzi gdy
γ13 < γ12 + γ 23
γ13 > γ12 − γ 23
•
Kąt zwilżania powierzchni definiujemy jako
γ12
γ13 = γ12 + γ 23 cos(θ)
θ
γ 23
γ13
Brak zwilżania
•
Kąt zwilżania powierzchni
γ12
γ13 = γ12 + γ 23 cos(θ)
θ
γ 23
•
Brak zwilżania powierzchni (A) zachodzi gdy
γ12 > γ13 + γ 23
γ13
Warunki stabilności (V,T)
• Układy zamknięty – warunek na stabilności - fluktuacje izotermicznoizochoryczne
δF ≥ 0
δF = − p1δV1 − p 2 δV1 + γδA + µ1δN1 + µ 2 δN 2 ≥ 0
N = N1 + N 2 = const
δN1 = −δN 2
V = V1 + V2 = const
δV1 = −V2
T = const
δT = 0
• Równania równowagi
p1 = p 2 + γ
δA
δV1
µ1 (p, T ) = µ 2 (p, T )
Stan równowagi zależy od kształtu powierzchni
Powierzchnia płaska
U1,V1,N1
U2,V2,N2
p1,T1,ρ
ρ1
p2,T2,ρ
ρ2
• Równania równowagi
p1 = p 2 + γ
δA
δV1
µ1 (p, T ) = µ 2 (p, T )
• Dla powierzchni płaskiej – wielkość powierzchni nie zależy od
objętości faz:
δA
=0
δV1
Warunki równowagi nie zależą od ich rozmiaru – są to wartości
umieszczane na diagramach fazowych
p1 = p 2
T1 = T2 = Tp
Powierzchnia zakrzywiona – przypadek izotropowy
• Równania równowagi
p1 = p 2 + γ
δA
δV1
U1,V1,N1
p1,T1,ρ
ρ1
µ1 (p, T ) = µ 2 (p, T )
U2,V2,N2
p2,T2,ρ
ρ2
• Fazy izotropowe - kula:
4πR 3
V1 =
3
A = 4πR
δA 2
= = κ1 + κ 2
δV1 R
2
κ1 , κ 2 - krzywizny powierzchni
Warunki równowagi zależą od rozmiaru faz
2γ
p1 = p 2 +
R
T1 = T2 ≠ Tp
Powierzchnia zakrzywiona – efekt Gibbsa-Thompsona
• Równania równowagi
2γ
p1 = p 2 +
R
U1,V1,N1
p1,T1,ρ
ρ1
• Przesunięcie ciśnienia – zmiana warunku
równowagi chemicznej
µ1 (p + dp, T + dT ) = µ 2 (p, T + dT )
Efekt Gibbsa - Thompsona – zmiana temperatury równowagi
powierzchni zakrzywionej
U2,V2,N2
p2,T2,ρ
ρ2
Efekt Gibbsa-Thompsona
• Powierzchnia płaska
• Powierzchnia zakrzywiona
µ1 (p, T ) = µ 2 (p, T )
µ1 (p + dp, T + dT ) = µ 2 (p, T + dT )
Po rozwinięciu otrzymujemy:
vdp − s1dT = s 2 dT
Tp dp
vdp
(V / N )dp
Vdp
=
=
=
dT =
s1 − s 2 (S1 − S2 ) / N S1 − S2
L
Efekt Gibbsa - Thompsona – zmiana temperatury równowagi powierzchni
zakrzywionej
 2 do 
T = Tp 1 
R


do =
γ
γ
=
- długość kapilarna
Tp (Sl - Ss ) L
L – ciepło przemiany na
jednostkę objętości
Powierzchnia zakrzywiona – przypadek anizotropowy
• Równania równowagi
R2
1
1 
p1 = p 2 + γ (θ, ϕ) +

R
R
2
 1
• Dla powierzchni są zdefiniowane dwa promienie
krzywizny R1 oraz R2 które dają rozmiar
obszaru fazy 2. Zmiana ta powoduje zmianę
potencjału chemicznego
R1
µ1 (p + dp, T + dT ) = µ 2 (p, T + dT )
Efekt Gibbsa - Thompsona – zmiana temperatury równowagi
powierzchni zakrzywionej:

1
1 

T = Tm 1 - d o (θ, ϕ) 
+
 R 1 R 2 

d o (θ, ϕ) =
γ (θ, ϕ)
γ (θ, ϕ)
=
Tm (Sl - Ss )
L
Przypadek anizotropowy - równowagowy kształt
powierzchni kryształów
•
•
W przypadku kryształów energią powierzchniowa zależy od orientacji, tzn.
zachodzi γ = γ(θ
θ,ϕ
ϕ)
Wykres tej zależności jest to tzw. γ - plot - wyznaczenie na jego podstawie
równowagowego kształtu kryształu nosi nazwę konstrukcji (twierdzenia)
Wulfa.
Równowagowy kształt kryształu jest wyznaczony przez minimalną obwiednię
utworzoną przez płaszczyzny prostopadłe do linii wychodzących ze środka wykresu
i przechodzące przez punkty przecięcia linii i tego wykresu
Stąd wyznaczenie równowagowego kształtu sprowadza się do wyznaczenia
zależności γ(θ,ϕ) .
dθ
E θ
1
E2
Konstrukcja Wulfa
• Dana jest zależność energii
powierzchniowej od kątów γ(θ
θ,ϕ
ϕ)
• Obliczamy wielkość energii
powierzchniowej dla kąta dθ
θ
• Dla przypadku 1
∆E 2 = E 2 dl ⊥
• Dla przypadku 1
E1dl ⊥
E1
∆E1 = E1dl1 =
=
dl ⊥
cos θ cos θ
W przypadku gdy E2 > (E1/cosθ) to realizowany będzie przypadek 1, w
przypadku odwrotnym przypadek 2.
Jest to konstrukcja Wulfa
Kryształ Kossela – najprostszy model kryształu
•
•
•
•
Siec kwadratowa (2d) lub regularna( 3d)
Oddziaływanie najbliższych sąsiadów
Energia oddziaływania nie zależy od kierunku
(φ
φ - energia wiązania dwu atomów)
Z – liczba sąsiadów (d=2 Z=4, d=3
Z=6)
φ
φ
• Modyfikacje
• Oddziaływanie anizotropowe
φ
φ
Y
• Oddziaływanie drugich sąsiadów
φ
X
φ
nnn
nn
Powierzchnie w krysztale Kossela
• Powierzchnia – układ atomów które nie maja wysycanych wiązań
(mają złamane wiązania - broken bonds )
• Energia kryształu (bez uwzględnienia
powierzchni):
φ
ES = −
ZN s φ
= − N bond −Sφ
2
• Energia kryształu (z powierzchnią):
E S+ A = −
N s Zφ
+ N bond − A φ
2
• Energia powierzchni:
E S+ A − E S = N bond − A φ
Jest to uproszczony lecz zupełny opis
powierzchni dla fazy stałej i fazy
gazowej
Powierzchnie kryształ-ciecz w modelu Kossela
• Energia wiązania atomów w krysztale - φss
N s Zφss
ES = −
= N bond −SSφss
2
• Energia wiązania atomów w cieczy - φll
N l Zφll
El = −
= N bond −llφll
2
•
Energia wiązania atomu w cieczy i w krysztale - φsl
• Energia układu z powierzchnią:
φss
φll
E S+ A + L =
φsl
− N bond −ls φls + − N bond −ss φss − N bond −llφll
• Każde wiązanie łączy dwa atomy, stąd
energia powierzchni jest równa:
φ + φss 

E A = N bond − A φsl − ll
2 

Jest to zupełny opis powierzchni dla fazy ciekłej i fazy stałej
Przykład (2d) - powierzchnie (01) oraz powierzchnie
nachylone (vicinal surfaces)
Powierzchnia (01)
Powierzchnia nachylona (vicinal)
α
1
tg(α ) =
n
n=
1
tg(α )
n – szerokość stopnia (w stałych sieciowych)
γ (α ) = φ(1 + n ) cos(α ) = [cos(α ) + sin (α ) ]φ ≥ φ
γ - plot – wykres ma wcięcie (cusp)
dla płaszczyzn o niskich wskaźnikach Millera (T = 0)
2-d kryształ Kossela - zależność kształtu od temperatury
kT/ϕ
ϕ=0
kT/ϕ
ϕ = 0.1
kT/ϕ
ϕ = 0.3
kT/ϕ
ϕ = 0.6
Powierzchnie 2-d oraz 3-d
• Stopień jest obiektem 1-d
Struktura powierzchni 3-d
F
S
K
• Powierzchnie o niskich wskaźnikach Millera nazywamy
powierzchniami płaskimi (F – flat)
• Warstwy atomowe zakończone są brzegiem. Brzeg warstwy
nazywamy stopniami (S – step lub L – ledge)
• Koniec rzędu atomów w stopniu nazywamy kinkiem (K – kink)
Model nosi nazwę modelu TLK – terrace – ledge - kink
Rodzaje powierzchni 3-d
Powierzchnia S(stepped)
Powierzchnia F(flat)
Powierzchnia K(kinked)
3-d Kossel –
klasyfikacja
Rotmana i
Wortisa
Diagram fazowy
Ciemne kropki - punkty osobliwe
przejścia od powierzchni gładkiej
do powierzchni zakrzywionej
Mikroskopowa struktura powierzchni – powierzchnie
gładkie i szorstkie
• Szorstkość powierzchni definiujemy jako:
N - No
R≡
No
gladka
N - ilość złamanych wiązań
No - minimalna ilość złamanych wiązań
szorstka
Parametr szorstkości zdefiniowany w ten sposób nie jest tożsamy z szorstkością
mierzona np. przy pomocy mikroskopu sił atomowych (AFM)
Przejście fazowe powierzchnia gładka – powierzchnia
szorstka: wyniki analityczne
• Model pojedynczej warstwy:
• Teoria pola średniego (przybliżenie Bragga – Williamsa)
• Energia swobodna układu jest równa:
F = kT[x ln x + (1 - x ) ln (1 - x ) + Z φ x (1 - x )]
0.1
0.0
x≡
Zφ/kT=3
-0.1
N at
No
F/kT
Zφ/kT=2
-0.2
-0.3
Przejście fazowe dla Zφ=2kT
Zφ/kT=1
-0.4
-0.5
0.0
0.2
0.4
0.6
x
0.8
1.0
Przejście fazowe powierzchnia gładka – powierzchnia
szorstka: wyniki symulacji komputerowych
•
Różnica energii
układu ze stopniami
oraz bez stopni:
Przejście fazowe
dla kT = 0.61φ
•
•
•
•
Model ze stopniami
Pseudoperiodyczne warunki brzegowe
Przybliżenie SOS
Leamy & Gilmer - 1974
α≡
kT kT
=
φ
ε
Równowagowa struktura stopni
• Stopień – obiekt 1-d
• Nie występuje przejście fazowe dla struktury
stopnia
• Stopień - obiekt szorstki – obecność dużej gęstości
kinków
• Stopień – obiekt na którym odbywa się wymiana
atomów
Powierzchnie kryształów rzeczywistych – bez atomów
obcych
• Na powierzchni kryształów rzeczywistych może zajść efekt
Jahna-Tellera: spontaniczne złamanie symetrii dla obniżenia
energii układu
• Wyróżniamy dwa rodzaje efektów: relaksację i rekonstrukcje
powierzchni
• Relaksacja powierzchni: zmiana położeń atomów zachowująca
symetrię translacyjną sieci (równoległą do powierzchni)
• Rekonstrukcja powierzchni: zmiana położeń atomów w sieci
naruszająca symetrie sieci Bravais
Relaksacja powierzchni
• Występuje w przypadku metali – wiązania prawie
izotropowe
• Zachowanie elektrostatycznej struktury powierzchni
Powierzchnia prosta
Powierzchnia zrelaksowana
Powierzchnie ulegające rekonstrukcji – przykłady
2x1 – rekonstrukcja
2x1 – rekonstrukcja
brakującego rzędu
parowania
Symetria sieci – notacja Wooda
Notacja (symbol) Wooda
Powierzchnia o wskaźnikach
krystalograficznych (hkl)
Symbol
chemiczny, np. C

S(hkl) κ


c – centrowana
p – prosta (domyślna w
przypadku braku symbolu)
a1 , a2 - wektory translacji
prymitywnych powierzchni
r r 
a1 a1  o
r , r  Rϕ
b1 b1 

Obrót o kąt ϕº
(Dla ϕ=0 symbol
jest pomijany)
b1 , b2 - wektory translacji
prymitywnych sieci objętościowej
Notacja Wooda jest niekiedy niejednoznaczna (dla sieci regularnej)
Symbol Wooda - przykłady
(1x1)
(2x 2)
(2x1)
(2x 2)
(
2x 2
)
Powierzchnie półprzewodników – rekonstrukcja
• Silne, kierunkowe wiązania
• Tendencja do wysycenia przez tworzenie wiązań
równoległych do powierzchni: łańcuchów, dimerów itp.
• Struktura powierzchni może ulec zmianie na skutek
przyłączenia obcych atomów wysycających złamane
wiązania
• Rekonstrukcja może sięgać kilku warstw atomowych
• Ładunki związane ze stanami powierzchniowymi tworzą
pola które mogą sięgać głęboko do wnętrza półprzewodnika
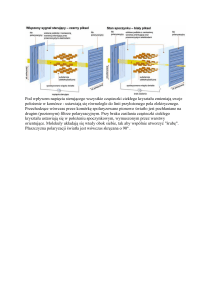
Powierzchnie półprzewodników - dimery
Dimery symetryczne - schemat powstawania
Dimery asymetryczne –
schemat powstawania
Skanningowy mikroskop tunelowy (Scanning Tunneling
Microscope – STM)
Nobel Laureates:
Heinrich Rohrer and
Gerd Binnig
Działanie skanningowego mikroskopu tunelowego
Oddziaływanie
końcówki mikroskopu
z powierzchnią
Zależność prądu tunelowania od
odległości d.
K oraz k – są stałymi
STM osiąga rozdzielczość atomową!
Mikroskop sił atomowych – (AFM – Atomic Force Microscope)
Atomic Force Microscope - NovaScan
ESPM II
OSPM II
Działanie mikroskopu sił atomowych
Oddziaływanie
końcówki mikroskopu
z powierzchnią
Detekcja ruchu
końcówki mikroskopu
– odbity promień lasera
Rozdzielczość atomowa
powierzchni miki w
roztworze wodnym.
Odległość pomiędzy
sąsiadującymi
wypukłościami wynosi
5.4 Å.
Powierzchnie półprzewodników – adatomy – Si (111) 7x7
DAS (dimer – adatom – stacking fault)
Adatomy na powierzchni Si (111) model
STM obraz
Adatomy – kółka szare
Si(111) – rekonstrukcja (7x7) - obrazy STM
3-d model
Model - R.M.
Tromp (IBM)
Obraz STM
Adsorpcja
• Fizysorpcja – przyłączanie atomów do powierzchni
kryształu/cieczy bez tworzenia wiązań chemicznych. Siły wiążące –
siły Lennarda – Jonesa. Na ogół nie prowadzi do lokalizacji atomu
na powierzchni
• Chemisorpcja –przyłączenie atomu do powierzchni
kryształu/cieczy powodujące powstanie wiązania chemicznego. Na
ogół prowadzi do lokalizacji atomów w węzłach sieci
krystalograficznej. Często prowadzi do zmian wiązania w
przyłączanych cząsteczkach chemicznych.
Fizysorpcja – izoterma Langmuira
•
•
•
•
Zakładamy ze istnieje pewna liczba węzłów na których mogą być
zaadsorbowane cząstki
Pokryciem Γ nazywamy stosunek liczby obsadzonych wezłów do liczby
wszystkich węzłów
Pokrycie zależy min. od energii wiązania na powierzchni
Dla danego układu (tzn. dla określonej energii wiązania) pokrycie jest
funkcja ciśnienia gazu nad powierzchnia i temperatury:
Γ = Γo
Γo = Γ(P → ∞ )
P
P + P1 2 (T )
1

E 
P1 2 (T ) = P Γ =  = CT 5 2 exp b 
2

 kT 
Eb – energia wiązania do powierzchni
Przykład - adsorpcja CO/Pd(111)
Chemisorpcja
• Adsorpcja dysocjatywna
25
25
20
20
15
15
E dis
10
5
E bar
E dis
10
E bar
5
0
1.0
Energy
Energy
• Adsorpcja molekularna
1.5
2.0
2.5
distance
3.0
3.5
4.0
0
1.0
1.5
2.0
2.5
distance
3.0
3.5
4.0
Oddziaływanie N2 z Ga(l)
N2
Energia bariery na rozpad
Excess energy [eV]
6
5.8 eV
4
N2 molecule
horizontally and
cluster of 19 atoms
In
Ga
Al
4.8 eV
2
3.2 eV
0
1
2
3
Distance from surface(A)
Ga
Energia dysocjacji swobodnej
cząsteczki N2 -- 9.8 eV/cząsteczkę
S. Krukowski and Z. Romanowski
Obliczenia kwantowe, Dmol, QM DFT
4
Dysocjacja N2 na powierzchni Ga
3,5
1.0A
N - N spacing [A]
3,0
2,5
2,0
1.6A
1,5
2.6A
1,0
0,8
1,2
1,6
2,0
2,4
2,8
3,2
3,6
d [A]
S. Krukowski and Z. Romanowski
Dmol, QM DFT
4,0
Podsumowanie
•
Powierzchnie, zwłaszcza powierzchnie półprzewodników tworzą struktury o
własnościach różnych od własności układów objętościowych
•
Równowagowe struktury powierzchni mogą wykazywać przemiany będące
przemianami fazowymi związanymi ze zmianą symetrii (rekonstrukcja).
Innego typu zmiany prowadzą do relaksacji powierzchni lub do zmiany jej
gładkości.
•
Wizualizacja struktury powierzchni wymaga zastosowanie zaawansowanych
technik mikroskopowych, np. AFM lub TEM
•
Adsorpcja gazów na powierzchni może zmieniać ich własności, w tym ich
strukturę w sposób zasadniczy
•
Adsorpcja cząsteczek może prowadzić do zmiany ich konformacji chemicznej
(chemisorpcja) lub tylko lokalizacji (fizysorpcja)
•
Otrzymanie właściwego obrazu powierzchni , w tym jej struktury oraz
procesów powierzchniowych wymaga przeprowadzenia obliczeń kwantowomechanicznych, najczęściej za pomocą metody DFT