Materiały piezoelektryczne: pomiar prostego i odwrotnego

Laboratorium Nowoczesna Diagnostyka Materiałowa
Materiały piezoelektryczne: pomiar prostego
i odwrotnego zjawiska piezoelektrycznego
Zagadnienia do przygotowania
1. Prosty i odwrotny efekt piezoelektryczny i układ równań opisujący te
efekty wraz z jednostkami zmiennych i parametrów materiałowych.
2. Podstawowe równania elektromechaniki.
3. Anizotropia w piezoelektrykach i podstawowe anizotropowe efekty piezoelektryczne.
4. Podstawowe geometrie rezonatorów piezoelektrycznych.
5. Metody pomiaru materiałów piezoelektrycznych.
Literatura
1. Wykład
Spis treści
Zagadnienia do przygotowania . . . . . . . . . . . . . . . . . . . . . . .
1
Literatura . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1
1. Wstęp . . . . . . . . . . . . . . . . . . . . . . . . .
1.1. Opis zjawisk piezoelektrycznych . . . . . . . .
1.2. Równania elektromechaniki . . . . . . . . . . .
1.3. Anizotropia zjawiska piezoelektrycznego . . . .
1.4. Rezonatory piezoelektryczne . . . . . . . . . .
1.5. Współczynnik sprzężenia elektromechanicznego
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
2
2
3
4
5
6
2. Program ćwiczenia . . . . . . . . . . . . . . . . . . . . . . .
2.1. Prosty efekt piezoelektryczny - pomiar statyczny . . . . .
2.2. Pomiary współczynnika sprzężenia elektromechanicznego
2.2.1. Na podstawie pomiarów pojemności . . . . . . . .
2.2.2. Ze wzorów Okami . . . . . . . . . . . . . . . . . .
2.3. Badanie odwrotnego efektu piezoelektrycznego . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
8
8
9
9
9
9
Materiały dodatkowe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
1
1. Wstęp
Zjawisko piezoelektryczności zostało odkryte w 1880 r. przez Pierre’a i Piotra Curie. Do
piezoelektryków należą do niektóre materiały krystaliczne, polimerowe i ceramiczne.
W przypadku materiałów krystalicznych, kryształy piezoelektryczne są układami nie posiadającymi środka symetrii. Wiele materiałów organicznych wykazuje efekt piezoelektryczny.
Może on być obserwowany w niektórych gatunkach drewna, jedwabiu i ścięgnach zwierzęcych.
Efekt występujący w materiałach pochodzenia naturalnego jest jednak bardzo słaby, w przeciwieństwie do niektórych tworzyw sztucznych, a zwłaszcza syntetycznych polimerów. Duże
znaczenie praktyczne mają cienkie folie tych materiałów, które mogą być prasowane w postaci stosów piezoelektrycznych. Efekt piezoelektryczny polimerów ulega zwiększeniu w wyniku
przeprowadzenia dodatkowych zabiegów, do których należy wyciąganie folii w podwyższonej
temperaturze i w dużym polu elektrycznym, jak również domieszkowanie tworzywa sztucznego
ceramiką piezoelektryczną.
Ceramiki piezoelektryczne są natomiast obecnie jednym z najszerzej stosowanych w technice
materiałów piezoelektrycznych. Szeroki zakres praktycznych zastosowań materiałów piezoceramicznych oprócz tego, że jest związany z właściwościami ceramik, tj. głównie z silnym efektem
piezoelektrycznym i w niektórych przypadkach z dużą wartością stałej dielektrycznej, wynika z łatwej i prostej technologii, która może być z powodzeniem stosowana w wielkoseryjnej
produkcji.
Najbardziej znanym piezoelektrykiem jest kryształ kwarcu, jednakże niektóre związki, jak
np. BaTiO3 lub PbZrTiO6 , wykazują ten efekt w znacznie większym stopniu (50 – 100 razy).
Piezoelektryki wykorzystywane są w różnych dziedzinach nauki i techniki. Najbardziej popularne to zastosowania to:
— w elementach elektronicznych (filtry, rezonatory)
— transformatory piezoelektryczne
— w zapalarkach do gazu, zapalniczkach – uderzenie ciężarka rozpędzonego przez napiętą
sprężynę a następnie zwolnioną przez zapadkę powoduje powstanie potencjału od kilku
do kilkunastu kV i przeskok iskry elektrycznej,
— precyzyjne wagi analityczne, wagi domowe,
— sterowanie pomiarem w tzw. mikroskopach STM czy AFM,
— wkładki gramofonowe w popularnych gramofonach z lat 1950-1990, gdzie drgania igły gramofonowej przenoszone na kryształy piezoelektryka, powodując powstanie napięć i uzyskanie
sygnału dźwiękowego,
— w sondach USG, które umożliwiają wytworzenie fali akustycznej i rejestrację ech, pochodzących od granic struktur o różnych wartościach impedancji akustycznych wzdłuż jednego
kierunku.
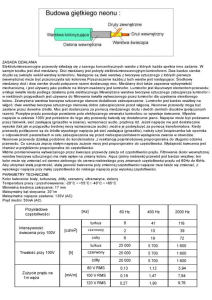
1.1. Opis zjawisk piezoelektrycznych
Polaryzacja elektryczna w wielu materiałach może wywołać zmiany wymiarów nieliniowo
zależne od polaryzacji, czyli efekt zwany elektrostrykcją. W niektórych dielektrykach, nazywanych piezoelektrykami, zachodzi zjawisko piezoelektryczne bądź też efekt piezoelektryczny
prosty i odwrotny.
Efekt piezoelektryczny prosty to zjawisko fizyczne polegające na powstawaniu na przeciwległych ścianach kryształów ładunków elektrycznych przeciwnego znaku w wyniku deformacji
kryształu.
Zjawisko to powstaje tylko w pewnych ciałach stałych, mających uporządkowaną budowę
atomową i wykazujących właściwą symetrię tej budowy. Zjawisko piezoelektryczne może zaist2
nieć w materiałach wykazujących samoistną lub indukowaną polaryzację. Polaryzacja ta zmienia
się pod wpływem naprężeń mechanicznych T, które powodują powstanie indukcji elektrycznej:
D =d·T
(1)
gdzie: D - indukcja elektryczna w mC2 , T - naprężenia mechaniczne w P a, d – moduł piezoelektryczny.
Efekt piezoelektryczny odwrotny to zjawisko polegające na zmianie wymiarów piezoelektryka pod wpływem zewnętrznego pola elektrycznego, który to efekt można opisać równaniem:
S =d·E
(2)
V
gdzie S - bezwymiarowe odkształcenie względne, E natężenie pola elektrycznego w m
. Wynika
stąd, że moduł piezoelektryczny d, nazywany również stałą ładunkową, można wyrazić na dwa
sposoby:
S
D
=
(3)
d=
T
E
C
a jego jednostkami mogą być zarówno N
jak i m
.1
V
1.2. Równania elektromechaniki
Ponieważ i naprężenia i pole elektryczne mogą oddziaływać na materiał jednocześnie, powyższe zależności należy powiązać. Formułuje się równania stanu, nazywane podstawowymi
równaniami elektromechaniki. Opisują one związki miedzy elektrycznymi i elastycznymi zmiennymi ośrodka, występującymi przy określonych warunkach brzegowych:
D = T · E + d · T
E
S =s ·T +d·E
(4a)
(4b)
F
, sE - podatność mechaniczna
gdzie T - przenikalność elektryczna dla stałych naprężeń w m
przy stałym natężeniu pola elektrycznego, wyrażana w P a−1 .
Równania stanu można wyrazić również dla innych zmiennych elastoelektrycznych:
S = sD · T + gt · D
(5a)
E = βT · D − g · T
(5b)
E
T = c · S + et · E
(5c)
D = S · E + e · S
(5d)
T = cD · S − ht · D
(5e)
S
E =β ·D−h·S
(5f)
W równaniach (4) - (5) występują:
— parametry mechaniczne materiałów takie jak moduł sprężystości c i jego odwrotność czyli
podatność mechaniczna d, a indeks górny E lub D oznacza warunki brzegowe, w jakich
zostały wyznaczone (przy stałym E lub D),
— parametry elektryczne, takie jak przenikalność elektryczna i jej odwrotność β, wyznaczone
dla stałego T (nazywane wolnymi) lub S (nazywane obciążonymi),
— współczynniki piezoelektryczne d – moduł piezoelektryczny i jego odwrotność h, g – stała
napięciowa i jej odwrotność e. 2
1
2
Wykaż samodzielnie, że istnieje równoważność pomiędzy tymi jednostkami.
Zastanów się, jakie jednostki będą miały parametry występujące w równaniach (5).
3
1.3. Anizotropia zjawiska piezoelektrycznego
Analizę zjawisk piezoelektrycznych komplikuje fakt, że zazwyczaj piezoelektryki są anizotropowe, to znaczy, że współczynniki mechaniczne, elektryczne i piezoelektryczne zależą od
kierunków działania sił i naprężeń.
Dla ceramiki piezoelektrycznej tensory D i E mają po trzy współrzędne (1 – 3), odpowiadające kierunkom układu współrzędnych x, y, z, natomiast tensory S i T mają po sześć
współrzędnych, związanych z naprężeniami i odkształceniami liniowymi w trzech osiach (1 –
3) oraz ścinającymi, również w trzech osiach (4 – 6). Dla materiałów anizotropowych równania
elektromechaniki przyjmują postać macierzową.
Dla materiałów ceramicznych występują pewne symetrie powodując, że niektóre z elementów
macierzy są równe 0 a inne powtarzają się. Dla typowej ceramiki piezoelektrycznej tensorowa
postać podstawowych równań elektromechaniki wygląda jak następująco:
S = sE · T + d · E
(6a)
T
D =d ·T +·E
gdzie
sE =
 E
s11
 E
s11
 E
s13

 0


 0
0
(6b)
E
0
0 d31
sE
0
0
0
12 s13


E
E


0 d31 
s11 s13 0
0
0

 0




11 0 0
E
E



0 d33 
0
0
s13 s13 0


d =  0

 0 d
 =  0 11 0 
0
0
0 sE
0
0
15



44
0 0 33






d
0
0
0
0
0 sE
0
15
44
E
0
0
0
0
0
0
0 2(sE
11 + s12 )



gdzie dT oznacza transpozycję macierzy współczynników d.
W takim równaniu współczynniki dik to moduły piezoelektryczne opisujące związek między
składową naprężeń mechanicznych Tk lub odkształceń mechanicznych Sk ze składową indukcji
elektrycznej Di lub natężenia pola elektrycznego Ei w identyczny sposób, jak równanie (4)
opisze to dla materiału izotropowego.
Jeśli w tensorach odkształceń, naprężeń czy pola elektrycznego niezerowa jest tylko jedna
składowa, wtedy równanie (6) silnie się upraszcza. W materiałach anizotropowych wyróżnia się
podstawowe kombinacje wyodrębnionych kierunków działania sił i pola elektrycznego:
— podłużny efekt piezoelektryczny, w którym kierunki naprężenia mechanicznego i indukcji
elektrycznej (polaryzacji) są zgodne a pozostałe równe zero, obowiązuje zatem w tym przypadku zależność:
S3
D3
=
(7)
d33 =
T3
E3
— poprzeczny efekt piezoelektryczny, w którym kierunki naprężenia mechanicznego i indukcji
elektrycznej (polaryzacji), są prostopadłe, obowiązuje zatem w tym przypadku zależność:
d31 =
D3
S1
=
T1
E3
(8)
— skośny efekt piezoelektryczny, w którym wektor polaryzacji jest równoległy do płaszczyzny,
w której zachodzi odkształcenie ścinające, obowiązuje zatem w tym przypadku zależność:
d15 =
D1
S5
=
T5
E1
Kierunki działania sił i pola elektrycznego w tych zjawiskach ilustruje rysunek 1.
4
(9)
a)
b)
T3
T3
T5
c)
Dl
Dl
Dl
P
E3
P
P
E1
E1
Rysunek 1. Rodzaje prostego i odwrotnego efektu piezoelektrycznego obserwowanego w piezoceramice: a) efekt podłużny, b) efekt poprzeczny, c) efekt skośny.
Rysunek 2. Podstawowe rodzaje drgań w rezonatorach piezoelektrycznych: a) drgania grubościowe, b) drgania poprzeczne, c) drgania radialne, d) drgania ścinania.
1.4. Rezonatory piezoelektryczne
Rezonatory piezoelektryczne to elementy elektroniczne, wykonane z piezoelektryków z naniesionymi na nie elektrodami, w których wykorzystuje się zależność impedancji takiego elementu
od częstotliwości.
Materiał piezoelektryczny jest w nich umieszczony tak, aby mógł się swobodnie odkształcać pod wpływem napięcia przyłożonego do elektrod rezonatora dzięki odwrotnemu zjawisku
piezoelektrycznemu. W normalnych warunkach i napięciach rzędu woltów odkształcenia te są
znikome, rzędu pikometra Jeśli jednak napięcie będzie przemienne a jego częstotliwość zbliżona do częstotliwości rezonansowej, to dzięki wzmocnieniu rezonansowemu odkształcenia staną
się znacznie większe. Wtedy ładunek generowany dzięki prostemu zjawisku odwrotnemu silnie
będzie wpływał na właściwości elektryczne rezonatora.
W rezonatorach mogą występować różne rodzaje wzbudzonych drgań, których przykłady
pokazano na rysunku 2.
Ich częstotliwości zależą od wymiarów rezonatora oraz prędkości rozchodzenia się fali akustycznej w materiale N (nazywaną również stałą częstotliwościową), z którego je wykonano. Na
przykład dla rezonatora o kształcie dysku o średnicy φ i grubości h częstotliwość rezonansowa
dla drgań radialnych wynosi:
N
(10)
fr =
φ
a grubościowych:
fr =
5
N
h
(11)
Wartość N również może zależeć od kierunku rozchodzenia się fali a jej typowe wartości dla
ceramik piezoelektrycznych to 1850 – 2000 m/s.
1.5. Współczynnik sprzężenia elektromechanicznego
Ważnym parametrem opisującym materiał piezoelektryczny jest współczynnik sprzężenia
elektromechanicznego k. Jest on bezwymiarową miarą stopnia przetwarzania energii elektrycznej w mechaniczną i odwrotnie w piezoelektryku. Można go określić na podstawie stosunku
wewnętrznej energii elektromechanicznej WEM do iloczynu energii zmagazynowanej w postaci
pola elektrycznego WE oraz energii mechanicznej (energii potencjalnej sprężystości) WM :
2
WEM
, gdzie:
WE · WM
J
1
1
WEM = S3 E3 = d33 E3 T3
2
2
m3
1
1
J
WE = E3 D3 = T33 E32
2
2
m3
J
1
1
2
T
WM = S3 T3 = sE
2
2 33 33 m3
k2 =
(12a)
(12b)
(12c)
(12d)
W zależności od materiału, rodzaju wzbudzonych drgań i warunków brzegowych przy jakich
pracuje element wykonany z materiału piezoelektrycznego liczbowe wartości k mogą osiągać
wartości od 0,01 do 0,75. Im ta wartość jest większa, tym większa skuteczność przetwarzania
energii elektrycznej w mechaniczną i odwrotnie.
Współczynnik ten można wyznaczyć na różne sposoby. Jeden z nich polega na pomiarze
przenikalności dielektrycznej wolnej T i obciążonej S piezoelektryka. Związek między tymi
właściwościami opisuje zależnosć:
S = T (1 − k 2 )
(13)
Jak wyznaczyć te dwie przenikalności elektryczne? Jeśli element piezoelektryczny ma regularny kształt, na przykład pastylki, na której elektrody umieszczone są np. jak na rysunku 2c,
wtedy łatwo jest wyliczyć przenikalność przez pomiar pojemności C na podstawie równania
opisującego pojemność kondensatora płaskiego:
C=
A
h
(14)
gdzie to przenikalność bezwzględna,3 A – pole powierzchni okładki kondensatora, h – odległość
pomiędzy okładkami, w tym wypadku grubość piezoelektryka.
Pojemność można dokładnie mierzyć za pomocą mierników RLC bądź analizatorów impedancji. W obu wypadkach do kondensatora przyłożone jest napięcie o zadanej częstotliwości i
na podstawie zmierzonego natężęnia przepływającego prądu wylicza się pojemność. Dla rezonatora wartość ta zależy od częstotliwości, przy której dokonuje się pomiaru, jak pokazano na
rysunku 3.
Jeśli element piezoelektryczny jest zamocowany swobodnie a częstotliwość, przy której dokonuje się pomiaru jest znacznie poniżej częstotliwości rezonansowej, wtedy piezoelektryk zdąży
się odkształcić przy każdym cyklu napięcia pomiarowego a swobodne zamocowanie spowoduje,
że brak będzie zewnętrznych naprężeń, które można uznać za stałe.
Gdy z drugiej strony częstotliwość pomiaru znacznie przekracza rezonansową, wtedy piezoelektryk nie nadąży się odkształcać. W ten sposób zmieniając częstotliwość dokonać pomiaru
C T oraz C S , z których na podstawie (14) można określić przenikalności T i S .
3
Przenikalność bezwzględna = 0 · r , gdzie 0 to przenikalność elektryczna próżni a r to przenikalność
elektryczna względna materiału.
6
pojemnosć
T
C
S
C
0
częstotliwość
Rysunek 3. Zależność pojemności rezonatora piezoelektrycznego od częstotliwości.
a)
b)
rezonator
R
R
aaaaaaa
aaaaaaa
aaaaaaa
aaaaaaa
aaaaaaa
rezonator
I
aaaaaaa
aaaaaaa
aaaaaaa
aaaaaaa
aaaaaaa
|Y|
|Z|
fr
fr
fa
częstotliwość
fa
częstotliwość
Rysunek 4. Dwa sposoby pomiaru krzywych rezonansowych za pomocą oscyloskopu w metodzie dynamicznej: a) pobudzenie napięciowe i pomiar prądu, b) pobudzenie prądowe i pomiar
napięcia.
Współczynnik sprzężenia elektromechanicznego można również wyznaczyć badając krzywe
rezonansowe rezonatora wykonanego z materiału piezoelektrycznego.
Krzywe te można wyznaczać w sposób przybliżony za pomocą prostych układów pomiarowych, pokazanych na rysunku 4. W układach tych generator funkcyjny pracuje jako wobulator,
czyli generator sygnału sinusoidalnego, o relatywnie dużej częstotliwości zmiennej w czasie, a
przykład w zakresie od 100 kHz do kilku MHz w ciągu 0,1 s.
Jeśli czas trwania kreślenia obrazu na ekranie oscyloskopu podłączonego do układu jak
na rysunku 4a to również będzie 0,1 s, wtedy uzyskamy przebieg, którego obwiednia będzie
odpowiadała natężeniu prądu I płynącego przez szeregowe połączenie rezonatora i rezystora. 4
Zakładając, że napięcie z generatora odkłada się w większości na rezonatorze można w przybliżeniu powiedzieć, że oscyloskop pokaże przebieg modułu admitancji Y = UI od częstotliwości.
Taki wykres można uzyskać również używając analizatora impedancji.
Na takim wykresie widoczne maksimum odpowiada częstotliwości, dla której następuje rezonans. Minimum odpowiada tzw. antyrezonansowi. Określając częstotliwości rezonansu fr i
antyrezonansu fa można określić współczynnik sprzężenia elektromechanicznego korzystając z
przybliżonej zależności podanej przez Okami:
1
=
k2
a
fa −fr
fr
+b
(15)
na podstawie której można obliczyć kr dla drgań radialnych podstawiając a = 0, 495, b = 0, 574
a k33 dla drgań grubościowych podstawiając a = 0, 405, b = 0, 810.
4
Prąd jest tu mierzony pośrednio, poprzez zastosowanie rezystora i obrazowanie na oscyloskopie napięcia
na rezystorze, przez który płynie ten prąd (U = R · I).
7
dźwignia
trzpień
przeciwwaga
belka
badany element
spust
podstawa
Rysunek 5. Stanowisko do pomiarów prostego efektu piezoelektrycznego metodą statyczną.
Jeśli pomiary przeprowadza się w układzie z pobudzeniem prądowym, pokazanym na rysunku 4b, wtedy na oscyloskopie obserwuje się wykres, którego obwiednia odpowiada w przybliżeniu
przebiegowi modułu impedancji Z = UI , rezonansowi odpowiada minimum a antyrezonansowi
maksimum.
2. Program ćwiczenia
2.1. Prosty efekt piezoelektryczny - pomiar statyczny
Zadanie polega na pomiarze ładunku wygenerowanego na elementach piezoelektrycznych,
umieszczonych w stanowisku pomiarowym (rysunek 5), na które wywierany jest nacisk związany z ciężarem użytych obciążników. Dostępne obciążenia: 100 g, 200 g, 200 g, 500 g, 1000 g
(obciążniki duże).
Akwizycja danych jest półautomatyczna (program piezo.vee). Program rejestruje wskazania elektrometru w czasie trwania pomiaru. Opcja ZERO CHECK powoduje zwarcie (opcja
uaktywniona) lub rozwarcie wejścia elektrometru. Procedura pomiaru:
1. Sprawdzić, czy nieobciążona belka nie naciska na mierzony element, w razie potrzeby wyregulować przeciwwagą.
2. Uruchomić program piezo.vee i nacisnąć START,
3. Zewrzeć wejście elektrometru zaznaczając opcję ZERO CHECK w programie.
4. Obrócić dźwignię (rysunek 5) do oporu w lewo.
5. Obciążyć mierzony element dobranymi ciężarkami umieszczanymi na trzpieniu.
6. Obrócić dźwignię z powrotem do oporu do pozycji pionowej.
7. Rozewrzeć wejście elektrometru usuwając zaznaczenie ZERO CHECK.
8. Przycisnąć spust, na element piezoelektryczny wywierany jest nacisk.
9. Po kilku sekundach ponownie zewrzeć wejście elektrometru (ZERO CHECK).
10. Powtórzyć algorytm pomiaru efektu piezoelektrycznego od punktu d) dla dostępnych obciążeń (od 100 g do 2000 g, a następnie od 2000 g do 100 g, z krokiem co 200 g).
11. Zapisane dane należy wykreślić. Z wykresu wyznaczyć wartości ładunku przy kolejnych
obciążeniach.
12. Sporządzić wykres zależności wygenerowanego ładunku od siły nacisku.
Na podstawie przeprowadzonej serii pomiarów należy wyznaczyć wartość modułu piezoelektrycznego d33 .
8
2.2. Pomiary współczynnika sprzężenia elektromechanicznego
2.2.1. Na podstawie pomiarów pojemności
Współczynnik sprzężenia elektromechanicznego można wyznaczyć poprzez pomiar pojemności C T i C S na podstawie równań (13) i (14). Dokonaj takich pomiarów dla elementu badanego
metodą statyczną i/lub innych elementów wskazanych przez prowadzącego.
2.2.2. Ze wzorów Okami
Wyznaczenie współczynnika sprzężenia elektromechanicznego dla wskazanych przez prowadzącego elementów piezoelektrycznych odbywa się w układzie, jak na rysunku 4.
Przed przystąpieniem do pomiarów należy zgrubnie oszacować częstotliwości, przy których
mogą wystąpić podstawowe typy rezonansów. Dokonuje się tego na podstawie równań (10) i
(11).
Przygotowanie układu pomiarowego do pracy wymaga zmian ustawień oscyloskopu:
1. zmienić metodę pomiaru na Peak-Detect (menu Acquire),
2. do kanału 1 dołączyć wyjście z badanego układu,
3. kanał 2 służy do synchronizacji z generatorem, należy go połączyć z odpowiednim wyjściem
generatora funkcyjnego, sprzężenie DC. Zbocze rosnące na tym sygnale oznacza początek
przemiatania, opadające wystepuje albo w połowie przemiatania, albo przy częstotliwości
ustawionej za pomocą funkcji MARKER w generatorze funkcyjnym.
Procedura pomiaru:
1. Na generatorze wybrać funkcję sinus o amplitudzie kilku VP P przemiatany liniowo od
100 kHz do np. 5 MHz w czasie np. 100 ms (dłuższe czasy dają mniej wygodny, ale dokładniejszy pomiar).
2. Ustawić odpowiednio wyzwalanie oscyloskopu na rosnące zbocze na kanale 2, a poziom
wyzwalania około połowy wysokości przebiegu na kanale 2. Podstawa czasu i położenie
wykresu w osi X należy ustawić tak, aby był widoczny jeden pełny cykl przemiatania. Jeśli
został ustawiony czas przemiatania 1 s lub dłuższy trzeba przełączyć tryb pracy wyzwalania
na NORMAL. W przeciwnym wypadku wygodniejszy jest tryb AUTO.
3. Na oscylogramie widoczne będą liczne rezonanse. Określić zgrubnie częstotliwość wszystkich
z nich w przedziale częstotliwości zadanym przez prowadzącego.
4. Na podstawie przeprowadzonych wcześniej oszacowań zidentyfikować rzeczywiste podstawowe drgania radialne i grubościowe.
5. Zmieniając wyłącznie ustawienia generatora zawęzić zakres przemiatania tak, aby na oscylogramie był widoczny wyłącznie podstawowy rezonans dla drgań radialnych. Zmierzyć częstotliwości rezonansu i antyrezonansu.
6. Wyznaczyć ze wzorów Okami (15) współczynnik sprzężenia elektromechanicznego dla drgań
radialnych.
7. Powtórzyć dwa poprzednie punkty dla podstawowych drgań grubościowych.
2.3. Badanie odwrotnego efektu piezoelektrycznego
Badanie odwrotnego efektu piezoelektrycznego odbywa się za pomocą stanowiska przedstawionego schematycznie na rysunku 6.
Elementem badanym jest piezostos. Składa się on z 78 warstw ceramiki piezoelektrycznej
przedzielonych elektrodami. Napięcie polaryzujące piezostos oddziałuje na każdą warstwę osobno przez co zmiana ∆l długości l piezostosu jest 78 razy większa, niż pojedynczej warstwy.
Górny koniec piezostosu zamocowany jest sztywno a koniec dolny oddziałuje na dźwignię
prostą, której przełożenie określa stosunek r2 do r1 . Do drugiego końca dźwigni zamocowano
ruchomą okładkę kondensatora, druga jego okładka jest nieruchoma. Ruchy dźwigni, wywołane
9
wskaźnik
zegarowy
piezoelement
l
dźwignia
r2
r1
h
śruba
nastawcza
kondensator
Rysunek 6. Schemat budowy stanowiska do pomiaru odwrotnego efektu piezoelektrycznego.
zmianą długości piezostosu ∆l powodują zmiany odległości h pomiędzy okładkami kondensatora.
Śruba nastawcza i wskaźnik zegarowy wykorzystywane są wyłącznie do kalibracji stanowiska,
przy normalnym pomiarze nie stykają się z dźwignią.
Pojemność kondensatora można mierzyć bezpośrednio odpowiednim miernikiem, bądź pośrednio, poprzez pomiar częstotliwości generatora RC, w którym za pojemność wzorcową dołączony jest kondensator pomiarowy. Częstotliwość sygnału z takiego generatora wynosi
f=
1
2RC
(16)
gdzie R to rezystor umieszczony w obwodzie generatora, którego wartość należy odczytać, a
pojemność C to:
0 A
k
C = C0 +
= C0 +
(17)
h + h0
h + h0
gdzie C0 to pojemność pasożytnicza kondensatora pomiarowego, niezależna od odległości h,
k – współczynnik kalibracyjny wynikający z powierzchni okładek kondensatora A, h0 – drugi
współczynnik kalibracyjny, uwzględniający niedokładności wykonania kondensatora. Wartości
współczynników wyznaczane są w czasie kalibracji, w której odległość między okładkami ustala
się śrubą nastawczą i mierzy wskaźnikiem zegarowym. Wartości współczynników kalibracyjnych
będą podane przez prowadzącego.
Jak wspomniano, w trakcie właściwych pomiarów czujnik zegarowy i śruba nastawcza nie
stykają się z dźwignią. Zmiany jej wychylenia określane są bezdotykowo, na podstawie pomiaru
częstotliwości generatora RC dokonywanych za pomocą multimetru. Zależność wiążącą h z f
należy wyprowadzić samodzielnie na podstawie (16) i (17).
W trakcie pomiarów należy:
1. Upewnić się, że wskaźnik zegarowy nie styka się z dźwignią.
2. Upewnić się, że piezostos znajduje się w kontakcie z dźwignią, a początkowa odległość
pomiędzy okładkami kondensatora pomiarowego jest taka, że częstotliwość f znajduje się
w przedziale od 7 do 10 kHz.
3. W sposób wskazany przez prowadzącego zajęcia określić zależność częstotliwości f of napięcia U przyłożonego do piezostosu.
4. Uwzględniając współczynniki kalibracyjne, przełożenie dźwigni oraz wielowarstwową budowę piezoelektryka, wykreślić zależność wydłużenia pojedynczej warstwy piezostosu od
napięcia.
5. Na podstawie tej zależności wyznaczyć wartość podłużnego modułu piezoelektrycznego d33 .
Materiały dodatkowe
10
Materiał
840 841 850 Typ IV 880
T
względna przenikalność elektryczna 33r 1250 1350 1900
3400
1000
współczynnik strat tgδ
0,40 0,35 1,40
1,70
0,35
◦
temperatura Curie [ C]
325 320 360
180
310
3
gęstość ρ[g/cm ]
7,6
7,6
7,6
7,6
7,6
dobroć mechaniczna Qm
500 1400 80
65
1000
współczynniki sprzężenia elektromechanicznego
kp
0,59 0,60 0,63
0,77
0,50
kt
0,59 0,60 0,63
0,77
0,50
k33
0,52
k31
0,72 0,68 0,72
0,62
k15
0,35 0,33 0,36
-h i h0,30i
moduły piezoelektryczne pC
, pm
N
V
d33
290 300 400
650
215
−d31
125 109 175
95
d15
480 450 590
- i h 330i
h
mV ·m
stałe ładunkowe
, mC
N
m2
g33
26,5 25,5 24,8
20,9
25,0
−g31
11,0 10,5 12,4
10,0
g15
38,0 35,0 36,0
28,0
moduły sprężystości [GPa]
c11
80
76
63
59
90
c33
68
63
54
51
72
h i
stałe częstotliwości drgań ms
NL
1524 1700 1500
1725
NT
2005 2005 2040
2040
2110
NP
2130 2055 2080
1980
2120
Tabela 1. Podstawowe parametry materiałowe wybranych ceramik piezoelektrycznych.
11