Podstawy Informatyki Metody dostepu do danych

Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Podstawy Informatyki
Metody dostępu do danych
dr inż. Alina MOMOT
[email protected]
http://zti.polsl.pl/AMomot/pi
dr inż. Alina MOMOT
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Plan wykładu
1
Informatyka
Wprowadzenie
Czym zajmuje się informatyka
2
Bazy danych
Wprowadzenie
Podstawowe problemy baz danych
Struktury danych
3
Przeszukiwanie tablic
Odszukanie rekordu
Przeszukiwanie sekwencyjne
Przeszukiwanie dychotomiczne
Przeszukiwanie z użyciem funkcji mieszającej
dr inż. Alina MOMOT
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Wprowadzenie
Czym zajmuje się informatyka
Informatyka - pochodzenie słowa
Informatyka pochodzi od francuskiego słowa informatique:
information (informacja) i automatique (automatyczny).
Pierwsze użycie słowa zarejestrowano w 1962 roku.
Pierwsza definicja (Akademia Francuska, 6 kwietnia 1967r.)
Informatyka
Nauka o racjonalnym przetwarzaniu, szczególnie przez maszynę,
automatyczną, informacji traktowanej jako nośnik wiadomości i podstawa
komunikowania się w dziedzinach technicznych, ekonomicznych i
społecznych.
dr inż. Alina MOMOT
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Wprowadzenie
Czym zajmuje się informatyka
Informatyka w Polsce
“(...) uświadomienie sobie istnienia odrębnej nauki obejmującej maszyny
matematyczne, maszynową technikę obliczeniową i przetwarzanie
informacji, określenie jej obszaru i powiązań z innymi naukami, a także
potrzeba krótkiej i jasnej nazwy – jest dzisiaj w Polsce nakazem
społecznym. Wydaje mi się, że najodpowiedniejszą nazwą dla tej
dziedziny w języku polskim jest INFORMATYKA (...)”
Romuald Marczyński
Sympozjum ’Naukowe Problemy Maszyn Matematycznych’
Zakopane, 20-26.10.1968 r.
dr inż. Alina MOMOT
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Wprowadzenie
Czym zajmuje się informatyka
Informatyka na świecie
Francja – informatique
Niemcy – Informatik
Polska – informatyka
Ale...
rosyjskie słowo informatika, oznacza informację naukowo-techniczną,
amerykańskie słowo informatics jest rozumiane jako information
science, czyli ’gromadzenie, klasyfikację, przechowywanie i
rozpowszechnianie zapisanej wiedzy’,
Odpowiednikiem słowa informatyka jest angielskie computer science.
dr inż. Alina MOMOT
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Wprowadzenie
Czym zajmuje się informatyka
Komputer - źródłosłów
Słowo komputer
pochodzi od łacińskiego computare (liczyć),
w XVII wieku poprzez francuskie compter zostało przejęte przez
język angielski.
Odpowiedniki w języku polskim:
pomoc obliczeniowa,
aparat matematyczny,
mózg elektronowy,
maszyna matematyczna,
elektroniczna maszyna obliczeniowa,
elektroniczna maszyna cyfrowa,
maszyna cyfrowa.
dr inż. Alina MOMOT
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Wprowadzenie
Czym zajmuje się informatyka
Pojęcie informatyki współcześnie
Informatykę można rozpatrywać jako:
samodzielną dyscyplinę naukową,
narzędzie wykorzystywane przez inne nauki,
gałąź techniki,
przemysł wytwarzający sprzęt i oprogramowanie.
dr inż. Alina MOMOT
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Wprowadzenie
Czym zajmuje się informatyka
Informatyka - definicja
Informatyka traktowana jako ’nauka o komputerach’, to jak chirurgia
nazwana ’nauką o nożu’.
[Dawid Harel]
Informatyka to systematyczne badanie procesów algorytmicznych,
które opisują i przetwarzają informację: ich teoria, analiza, projektowanie,
efektywność, implementacja i zastosowanie.
Fundamentalne pytanie brzmi: co można (efektywnie) zautomatyzować?
[prof. Jan Węglarz]
dr inż. Alina MOMOT
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Wprowadzenie
Czym zajmuje się informatyka
Czym zajmuje się informatyka
Informatyka zajmuje się zagadnieniami związanymi z
pobieraniem,
przechowywaniem,
przetwarzaniem,
przesyłaniem informacji.
[prof. Stefan Węgrzyn]
Informacja :
wszystko to co zmniejsza naszą niepewność,
uporządkowane dane, zinterpretowane na podstawie posiadanej
wiedzy.
[prof. Władysław M. Turski]
dr inż. Alina MOMOT
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Wprowadzenie
Podstawowe problemy baz danych
Struktury danych
Plan wykładu
1
Informatyka
Wprowadzenie
Czym zajmuje się informatyka
2
Bazy danych
Wprowadzenie
Podstawowe problemy baz danych
Struktury danych
3
Przeszukiwanie tablic
Odszukanie rekordu
Przeszukiwanie sekwencyjne
Przeszukiwanie dychotomiczne
Przeszukiwanie z użyciem funkcji mieszającej
dr inż. Alina MOMOT
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Wprowadzenie
Podstawowe problemy baz danych
Struktury danych
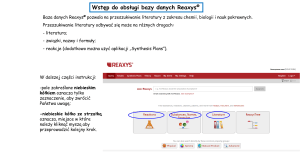
Bazy danych
Najwcześniejsze znane użycie terminu baza danych miało miejsce w
listopadzie 1963.
Baza danych - uporządkowany zbiór danych przechowywany w
pamięci komputera.
Przetwarzanie danych realizowane jest za pomocą programu
zarządzającego (system zarządzania bazą danych).
Dane reprezentowane są przez rekordy danych stanowiące
uporządkowany zbiór elementów dowolnego typu umieszczony w
tzw. polach, które zawierają klucz rekordu oraz jego atrybuty.
dr inż. Alina MOMOT
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Wprowadzenie
Podstawowe problemy baz danych
Struktury danych
Modele baz danych
Pierwsze systemy zarządzania bazami danych opracowano w latach
60-tych XXw.
Charles Bachman szukał bardziej efektywnego użycia nowych
urządzeń umożliwiających bezpośredni dostęp do składowanych
danych.
Powstały wtedy pierwsze modele baz danych:
hierarchiczne
– jednej danej przyporządkowanych jest m innych danych bazy,
sieciowe
– n danym przyporządkowanych jest m innych danych bazy,
relacyjne (F.Codd, lata 70-te)
– zależności między danymi opisywane są poprzez odpowiednie klucze,
obiektowe (lata 90-te).
dr inż. Alina MOMOT
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Wprowadzenie
Podstawowe problemy baz danych
Struktury danych
Podstawowe problemy baz danych
1
Problem rozmieszczenia polega na podaniu takiego algorytmu A,
który na podstawie klucza Ki zawartego w rekordzie Ri przydzieli
miejsce (adres) dla tegoż rekordu w określonej strukturze S.
2
Problem odszukania rekordu Ri w strukturze S polega na ustaleniu
adresu tego rekordu, na podstawie klucza Ki i algorytmu A.
3
Problem wyszukania występuje, gdy na podstawie atrybutów
innych niż klucz należy wyszukać odpowiedni rekord1 .
1
rozwiązanie tego problemu polega na przetestowaniu pól wszystkich rekordów i
porównaniu ich zawartości z wartością zadanego atrybutu
dr inż. Alina MOMOT
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Wprowadzenie
Podstawowe problemy baz danych
Struktury danych
Struktury danych
Podstawowe struktury danych to:
struktury stałe
ich rozmiar jest niezależny od zebranych w nich elementów, ustalony
z góry i niezmienny w czasie wykonywania operacji na strukturze,
m.in. tablice
struktury dynamicznie zmienne
ich rozmiar zależy od liczby zgromadzonych w nich elementów, m.in.
listy, drzewa, sieci.
Rekordy w takich strukturach mają jedno lub kilka dodatkowych pól,
zwanych polami łącznikowymi lub wskaźnikowymi, zwykle
zawierające adresy elementów połączonych z danym rekordem.
dr inż. Alina MOMOT
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Wprowadzenie
Podstawowe problemy baz danych
Struktury danych
Tablice
Jest strukturą jednorodną.
Składa się ze składowych tego samego typu zwanego podstawowym.
Jest strukturą o dostępie swobodnym (wszystkie elementy mogą być
wybrane w dowolnej kolejności i są jednakowo dostępne).
Tablica jednowymiarowa o rozmiarze n oznaczana jest T[n].
Pesel
34567890123
45678901234
56789012345
67890123456
Nazwisko
Kowalska
Nowak
Testowy
Kowalska
Imię
Anna
Tomasz
Jan
Anna
Adres
Gliwice
Katowice
Bytom
Gliwice
Tablicę dwuwymiarową T[m,n] przedstawiamy jako m szeregowo
ustawionych tablic o rozmiarze n.
dr inż. Alina MOMOT
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Wprowadzenie
Podstawowe problemy baz danych
Struktury danych
Listy
Lista liniowa – zbiór, w którym każdy element ma co najwyżej
jednego poprzednika lub następnika.
Szczególnymi przypadkami listy liniowej są:
lista cykliczna
– nie można tu wyróżnić początkowego ani końcowego elementu,
stos
– dopisywanie i usuwanie elementów odbywa się z jednego końca,
kolejka
– rekordy są dopisywane z jednego końca a usuwane z drugiego
(tzn. usunięty może być tylko najwcześniej wpisany element).
Lista dwukierunkowa – istnieje tu dodatkowe w stosunku do listy
liniowej połączenie ’następnik-poprzednik’.
dr inż. Alina MOMOT
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Wprowadzenie
Podstawowe problemy baz danych
Struktury danych
Drzewa, sieci
Drzewo – struktura, w której element może posiadać wiele następników,
lecz tylko jednego poprzednika.
Drzewo binarne – liczba następników wynosi zero, jeden lub dwa.
Drzewo BST (ang. Binary Search Tree) – drzewo binarne, w
którym lewe poddrzewo każdego węzła zawiera wyłącznie elementy o
kluczach mniejszych niż klucz węzła a prawe poddrzewo zawiera
wyłącznie elementy o kluczach większych.
Drzewo AVL (Adelsona-Velskiego oraz Landisa) – zrównoważone
binarne drzewo poszukiwań (BST), w którym wysokość lewego i
prawego poddrzewa każdego węzła różni się co najwyżej o jeden.
Sieć – struktura, w której istnieją elementy o wielu poprzednikach i wielu
następnikach.
dr inż. Alina MOMOT
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Wprowadzenie
Podstawowe problemy baz danych
Struktury danych
Przykłady drzew binarnych
dr inż. Alina MOMOT
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Odszukanie rekordu
Przeszukiwanie sekwencyjne
Przeszukiwanie dychotomiczne
Przeszukiwanie z użyciem funkcji mieszającej
Plan wykładu
1
Informatyka
Wprowadzenie
Czym zajmuje się informatyka
2
Bazy danych
Wprowadzenie
Podstawowe problemy baz danych
Struktury danych
3
Przeszukiwanie tablic
Odszukanie rekordu
Przeszukiwanie sekwencyjne
Przeszukiwanie dychotomiczne
Przeszukiwanie z użyciem funkcji mieszającej
dr inż. Alina MOMOT
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Odszukanie rekordu
Przeszukiwanie sekwencyjne
Przeszukiwanie dychotomiczne
Przeszukiwanie z użyciem funkcji mieszającej
Odszukanie rekordu danego kluczem
dr inż. Alina MOMOT
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Odszukanie rekordu
Przeszukiwanie sekwencyjne
Przeszukiwanie dychotomiczne
Przeszukiwanie z użyciem funkcji mieszającej
Odszukanie rekordu danego kluczem
Sposób odszukania zależy od struktury.
Najprostszy przypadek gdy klucz jednocześnie adresem rekordu
(indeksem) – metoda adresowania bezpośredniego.
Niskie zapełnienie obszaru pamięci przeznaczonego na zbiór.
Problemy podczas przemieszczania zbioru w pamięci i jego
rozszerzania.
dr inż. Alina MOMOT
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Odszukanie rekordu
Przeszukiwanie sekwencyjne
Przeszukiwanie dychotomiczne
Przeszukiwanie z użyciem funkcji mieszającej
Odszukanie rekordu w tablicy
Założenia:
N-elementowy zbiór rekordów umieszczony w N-elementowej tablicy.
Przy braku dodatkowej wiedzy tablicę przeszukuje się sekwencyjnie.
wyszukiwanie liniowe
function Szukaj(x, T[1..N])
begin
for i:=1 to N do
if T[i]=x return i;
return ’brak poszukiwanego elementu’;
end
W pesymistycznym przypadku lub gdy tablica nie zawiera poszukiwanego
elementu koszt czasowy wynosi N.
dr inż. Alina MOMOT
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Odszukanie rekordu
Przeszukiwanie sekwencyjne
Przeszukiwanie dychotomiczne
Przeszukiwanie z użyciem funkcji mieszającej
Średni czas odszukania
Średni czas odszukania opisuje wzór:
L=
N
X
ci pi ,
i=1
gdzie:
ci – liczba prób wykonanych w celu odnalezienia i-tego rekordu,
pi – prawdopodobieństwo odwołania do i-tego rekordu,
N – wielkość (pojemność) tablicy.
dr inż. Alina MOMOT
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Odszukanie rekordu
Przeszukiwanie sekwencyjne
Przeszukiwanie dychotomiczne
Przeszukiwanie z użyciem funkcji mieszającej
Średni czas odszukania - wyszukiwanie liniowe
Założenia:
prawdopodobieństwo odwołania do każdego z rekordów jest
jednakowe.
L=
N
X
i=1
ci pi =
N
X
i
i=1
dr inż. Alina MOMOT
N
=
N +1
= O(N)
2
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Odszukanie rekordu
Przeszukiwanie sekwencyjne
Przeszukiwanie dychotomiczne
Przeszukiwanie z użyciem funkcji mieszającej
Odszukanie rekordu w tablicy
Wiedząc, że N-elementowa tablica jest uporządkowana rosnąco można
zastosować przeszukiwanie dychotomiczne.
wyszukiwanie binarne
function Szukaj(x, T[1..n])
begin
l:=1;r:=n;
while (l<=r) do begin
m:=(l+r) div 2;
if (T[m]<x) then l:=m+1
else if (T[m]>x) then r:=m-1
else return m; { ponieważ T[m]=x }
end;
return ’brak poszukiwanego elementu’;
end;
dr inż. Alina MOMOT
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Odszukanie rekordu
Przeszukiwanie sekwencyjne
Przeszukiwanie dychotomiczne
Przeszukiwanie z użyciem funkcji mieszającej
Przeszukiwanie dychotomiczne - przykład
Szukany klucz: 9
(left) l = 1
(right) r = 10
(middle) m = (1 + 10) div 2 = 5
1
2
3
4
5
dr inż. Alina MOMOT
6
7
8
9
Synchronizacja procesów
10
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Odszukanie rekordu
Przeszukiwanie sekwencyjne
Przeszukiwanie dychotomiczne
Przeszukiwanie z użyciem funkcji mieszającej
Przeszukiwanie dychotomiczne - przykład
Szukany klucz: 9
(left) l = 6
(right) r = 10
(middle) m = (6 + 10) div 2 = 8
1
2
3
4
5
dr inż. Alina MOMOT
6
7
8
9
Synchronizacja procesów
10
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Odszukanie rekordu
Przeszukiwanie sekwencyjne
Przeszukiwanie dychotomiczne
Przeszukiwanie z użyciem funkcji mieszającej
Przeszukiwanie dychotomiczne - przykład
Szukany klucz: 9
(left) l = 9
(right) r = 10
(middle) m = (9 + 10) div 2 = 9
1
2
3
4
5
dr inż. Alina MOMOT
6
7
8
9
Synchronizacja procesów
10
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Odszukanie rekordu
Przeszukiwanie sekwencyjne
Przeszukiwanie dychotomiczne
Przeszukiwanie z użyciem funkcji mieszającej
Przeszukiwanie dychotomiczne - przykład c.d.
Szukany klucz: 5
liczba prób: 1
1
2
3
4
5
6
7
8
9
10
5
dr inż. Alina MOMOT
krok 1
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Odszukanie rekordu
Przeszukiwanie sekwencyjne
Przeszukiwanie dychotomiczne
Przeszukiwanie z użyciem funkcji mieszającej
Przeszukiwanie dychotomiczne - przykład c.d.
Szukany klucz: 8
liczba prób: 2
1
2
3
4
5
6
7
8
9
10
5
2
krok 1
8
dr inż. Alina MOMOT
Synchronizacja procesów
krok 2
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Odszukanie rekordu
Przeszukiwanie sekwencyjne
Przeszukiwanie dychotomiczne
Przeszukiwanie z użyciem funkcji mieszającej
Przeszukiwanie dychotomiczne - przykład c.d.
Szukany klucz: 6
liczba prób: 3
1
2
3
4
5
6
7
8
9
10
5
krok 1
2
1
8
3
6
dr inż. Alina MOMOT
krok 2
9
Synchronizacja procesów
krok 3
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Odszukanie rekordu
Przeszukiwanie sekwencyjne
Przeszukiwanie dychotomiczne
Przeszukiwanie z użyciem funkcji mieszającej
Przeszukiwanie dychotomiczne - przykład c.d.
Szukany klucz:
liczba prób: 4
1
2
3
4
7
5
6
7
8
9
10
5
krok 1
2
1
8
3
6
4
dr inż. Alina MOMOT
krok 2
9
7
krok 3
10
Synchronizacja procesów
krok 4
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Odszukanie rekordu
Przeszukiwanie sekwencyjne
Przeszukiwanie dychotomiczne
Przeszukiwanie z użyciem funkcji mieszającej
Przeszukiwanie dychotomiczne - przykład c.d.
Szukany klucz:
liczba prób:
1
2
3
4
5
6
7
8
9
10
5
krok 1
2
1
8
3
6
4
krok 2
9
7
krok 3
10
krok 4
Powstało drzewo binarne idealnie zrównoważone.
dr inż. Alina MOMOT
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Odszukanie rekordu
Przeszukiwanie sekwencyjne
Przeszukiwanie dychotomiczne
Przeszukiwanie z użyciem funkcji mieszającej
Średni czas odszukania - wyszukiwanie binarne
Odszukanie rekordu w przypadku:
optymistycznym wymaga 1 próby,
pesymistycznym wymaga dlog2 (N + 1)e prób.
Średni czas odszukania rekordu:
L=
N
X
ci pi = O(log2 (N)).
i=1
dr inż. Alina MOMOT
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Odszukanie rekordu
Przeszukiwanie sekwencyjne
Przeszukiwanie dychotomiczne
Przeszukiwanie z użyciem funkcji mieszającej
Średni czas odszukania - drzewo BST
Wyszukiwanie w drzewie binarnym w przypadku:
optymistycznym wymaga 1 próby,
pesymistycznym wymaga N prób
drzewo degeneruje się do listy, np. dla posortowanych danych.
Średnio liczba prób wynosi:
L = 2(log2 (N) + γ) − 3,
gdzie γ ≈ 0.577 jest stałą Eulera.
Drzewo wyważone skraca nam drogę poszukiwań średnio o 39%.
dr inż. Alina MOMOT
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Odszukanie rekordu
Przeszukiwanie sekwencyjne
Przeszukiwanie dychotomiczne
Przeszukiwanie z użyciem funkcji mieszającej
Funkcja mieszająca (haszująca)
Funkcja mieszająca dla danego klucza wyznacza indeks w tablicy
(przekształca klucz w liczbę z zadanego zakresu).
Zbiór możliwych wartości kluczy jest najczęściej znacznie większy od
zbioru adresów (indeksów tablicy)!
dr inż. Alina MOMOT
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Odszukanie rekordu
Przeszukiwanie sekwencyjne
Przeszukiwanie dychotomiczne
Przeszukiwanie z użyciem funkcji mieszającej
Funkcja mieszająca - przykłady
1
Przekształcenie klucza do postaci liczby binarnej, np. dla klucza
literowego można skorzystać z kodu ASCII.
2
W przypadku klucza binarnego:
wyznaczenie reszty z dzielenia wartości liczbowej klucza przez liczbę
elementów tablicy N,
odrzucenie najmniej znaczących bitów (lub skrajnych bitów),
podzielenie klucza binarnego na kilka części i dodanie ich do siebie,
podnoszenie wartości klucza do kwadratu, a następnie pobieranie do
wyniku tylko wybranych bitów.
dr inż. Alina MOMOT
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Odszukanie rekordu
Przeszukiwanie sekwencyjne
Przeszukiwanie dychotomiczne
Przeszukiwanie z użyciem funkcji mieszającej
Odszukanie rekordu z użyciem funkcji mieszającej
1
Mając zadany klucz K należy obliczyć związany z nim adres (indeks).
2
Sprawdzić, czy obiekt o kluczu K jest rzeczywiście pod adresem
wyznaczonym przez funkcję h(K).
Kolizja występuje gdy pod danym adresem jest inny klucz niż żądany.
Wyznacza się wtedy adres alternatywny za pomocą odpowiedniego
algorytmu rozwiązywania kolizji.
dr inż. Alina MOMOT
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Odszukanie rekordu
Przeszukiwanie sekwencyjne
Przeszukiwanie dychotomiczne
Przeszukiwanie z użyciem funkcji mieszającej
Rozwiązywanie problemu kolizji - metoda łańcuchowa
Dane nie są przechowywane bezpośrednio w tablicy, lecz na liście
związanej z danym indeksem tablicy.
Nowy element dołącza się do końca listy.
Średnia złożoność wyszukiwania jest złożonością liniowego
wyszukiwania elementu na liście i zależy od współczynnika
wypełnienia listy1 .
Ponieważ złożoność pesymistyczna wyszukiwania wynosi O(N),
czasami zamiast list stosuje się drzewa.
Zaletą metody łańcuchowej jest szybkość i prostota usuwania
elementów z listy.
1
stosunek liczby elementów do wielkości tablicy
dr inż. Alina MOMOT
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Odszukanie rekordu
Przeszukiwanie sekwencyjne
Przeszukiwanie dychotomiczne
Przeszukiwanie z użyciem funkcji mieszającej
Rozwiązywanie problemu kolizji - adresowanie otwarte
Lokalizacja elementu określana jest przez dodanie do wartości funkcji
mieszającej h(K ) wartości funkcji przyrostu p(i).
i oznacza numer próby (ile razy wstawienie się nie powiodło ze
względu na kolizję),
Ze względu na rodzaj funkcji przyrostu wyróżnia się różne metody
adresowania otwartego, np.:
szukanie liniowe, dla p(i) = i,
szukanie kwadratowe, dla p(i) = i 2 ;
mieszanie podwójne, dla p(i) = i ∗ h0 (K ),
gdzie h0 jest dodatkową funkcją mieszającą od klucza K .
Wadą tej metody jest problem usuwania elementu, w sytuacji gdy w
tablicy znajdują się inne, o tej samej wartości funkcji mieszającej.
dr inż. Alina MOMOT
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Odszukanie rekordu
Przeszukiwanie sekwencyjne
Przeszukiwanie dychotomiczne
Przeszukiwanie z użyciem funkcji mieszającej
Analiza efektywności funkcji mieszającej - założenia
Wystąpienie każdego z kluczy jednakowo prawdopodobne.
Tablica o rozmiarze N zawiera już n rekordów.
Funkcja mieszająca przydziela wszystkie miejsca w tablicy z
jednakowym prawdopodobieństwem, czyli 1/N.
Algorytm rozwiązywania kolizji wybiera nie przeszukane miejsca w
tablicy z równym prawdopodobieństwem.
dr inż. Alina MOMOT
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Odszukanie rekordu
Przeszukiwanie sekwencyjne
Przeszukiwanie dychotomiczne
Przeszukiwanie z użyciem funkcji mieszającej
Analiza efektywności funkcji mieszającej
Spodziewana średnia liczba prób jaką należy wykonać aby umieścić n+1
rekord w tablicy N-elementowej:
Dla n = 0 otrzymujemy E1 = 1, bo tablica była jeszcze pusta.
1 N−1
N+1
Dla n = 1, E2 = 1Pt (1) + 2Pn (1)Pt (2) = N−1
N + 2 N N−1 = N .
Dla n = 2, E3 = 1Pt (1) + 2Pn (1)Pt (2) + 3Pn (1)Pn (2)Pt (3) =
Dla n = 3, E4 = 1Pt (1) + . . . + 4Pn (1)Pn (2)Pn (3)Pt (4) =
Ogólnie
N+1
En+1 =
N−n+1
N+1
N−1
N+1
N−2
Pt (j) – prawdopodobieństwo, że udało się wstawić rekord w j-tym kroku
pod warunkiem, że w żadnym poprzednim się nie udało,
Pn (j) – prawdopodobieństwo, że w j-tym kroku się nie udało wstawić
rekordu pod warunkiem, że w żadnym poprzednim kroku się nie udało.
dr inż. Alina MOMOT
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Odszukanie rekordu
Przeszukiwanie sekwencyjne
Przeszukiwanie dychotomiczne
Przeszukiwanie z użyciem funkcji mieszającej
Analiza efektywności funkcji mieszającej
Spodziewana średnia liczba prób jaką należy wykonać aby umieścić n+1
rekord w tablicy N-elementowej:
Dla n = 0 otrzymujemy E1 = 1, bo tablica była jeszcze pusta.
1 N−1
N+1
Dla n = 1, E2 = 1Pt (1) + 2Pn (1)Pt (2) = N−1
N + 2 N N−1 = N .
Dla n = 2, E3 = 1Pt (1) + 2Pn (1)Pt (2) + 3Pn (1)Pn (2)Pt (3) =
Dla n = 3, E4 = 1Pt (1) + . . . + 4Pn (1)Pn (2)Pn (3)Pt (4) =
Ogólnie
N+1
En+1 =
N−n+1
N+1
N−1
N+1
N−2
Pt (j) – prawdopodobieństwo, że udało się wstawić rekord w j-tym kroku
pod warunkiem, że w żadnym poprzednim się nie udało,
Pn (j) – prawdopodobieństwo, że w j-tym kroku się nie udało wstawić
rekordu pod warunkiem, że w żadnym poprzednim kroku się nie udało.
dr inż. Alina MOMOT
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Odszukanie rekordu
Przeszukiwanie sekwencyjne
Przeszukiwanie dychotomiczne
Przeszukiwanie z użyciem funkcji mieszającej
Analiza efektywności funkcji mieszającej
Spodziewana średnia liczba prób jaką należy wykonać aby umieścić n+1
rekord w tablicy N-elementowej:
Dla n = 0 otrzymujemy E1 = 1, bo tablica była jeszcze pusta.
1 N−1
N+1
Dla n = 1, E2 = 1Pt (1) + 2Pn (1)Pt (2) = N−1
N + 2 N N−1 = N .
Dla n = 2, E3 = 1Pt (1) + 2Pn (1)Pt (2) + 3Pn (1)Pn (2)Pt (3) =
Dla n = 3, E4 = 1Pt (1) + . . . + 4Pn (1)Pn (2)Pn (3)Pt (4) =
Ogólnie
N+1
En+1 =
N−n+1
N+1
N−1
N+1
N−2
Pt (j) – prawdopodobieństwo, że udało się wstawić rekord w j-tym kroku
pod warunkiem, że w żadnym poprzednim się nie udało,
Pn (j) – prawdopodobieństwo, że w j-tym kroku się nie udało wstawić
rekordu pod warunkiem, że w żadnym poprzednim kroku się nie udało.
dr inż. Alina MOMOT
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Odszukanie rekordu
Przeszukiwanie sekwencyjne
Przeszukiwanie dychotomiczne
Przeszukiwanie z użyciem funkcji mieszającej
Analiza efektywności funkcji mieszającej
Spodziewana średnia liczba prób jaką należy wykonać aby umieścić n+1
rekord w tablicy N-elementowej:
Dla n = 0 otrzymujemy E1 = 1, bo tablica była jeszcze pusta.
1 N−1
N+1
Dla n = 1, E2 = 1Pt (1) + 2Pn (1)Pt (2) = N−1
N + 2 N N−1 = N .
Dla n = 2, E3 = 1Pt (1) + 2Pn (1)Pt (2) + 3Pn (1)Pn (2)Pt (3) =
Dla n = 3, E4 = 1Pt (1) + . . . + 4Pn (1)Pn (2)Pn (3)Pt (4) =
Ogólnie
N+1
En+1 =
N−n+1
N+1
N−1
N+1
N−2
Pt (j) – prawdopodobieństwo, że udało się wstawić rekord w j-tym kroku
pod warunkiem, że w żadnym poprzednim się nie udało,
Pn (j) – prawdopodobieństwo, że w j-tym kroku się nie udało wstawić
rekordu pod warunkiem, że w żadnym poprzednim kroku się nie udało.
dr inż. Alina MOMOT
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Odszukanie rekordu
Przeszukiwanie sekwencyjne
Przeszukiwanie dychotomiczne
Przeszukiwanie z użyciem funkcji mieszającej
Analiza efektywności funkcji mieszającej
Spodziewana średnia liczba prób jaką należy wykonać aby umieścić n+1
rekord w tablicy N-elementowej:
Dla n = 0 otrzymujemy E1 = 1, bo tablica była jeszcze pusta.
1 N−1
N+1
Dla n = 1, E2 = 1Pt (1) + 2Pn (1)Pt (2) = N−1
N + 2 N N−1 = N .
Dla n = 2, E3 = 1Pt (1) + 2Pn (1)Pt (2) + 3Pn (1)Pn (2)Pt (3) =
Dla n = 3, E4 = 1Pt (1) + . . . + 4Pn (1)Pn (2)Pn (3)Pt (4) =
Ogólnie
N+1
En+1 =
N−n+1
N+1
N−1
N+1
N−2
Pt (j) – prawdopodobieństwo, że udało się wstawić rekord w j-tym kroku
pod warunkiem, że w żadnym poprzednim się nie udało,
Pn (j) – prawdopodobieństwo, że w j-tym kroku się nie udało wstawić
rekordu pod warunkiem, że w żadnym poprzednim kroku się nie udało.
dr inż. Alina MOMOT
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Odszukanie rekordu
Przeszukiwanie sekwencyjne
Przeszukiwanie dychotomiczne
Przeszukiwanie z użyciem funkcji mieszającej
Wykres En+1 dla 100-elementowej tablicy
dr inż. Alina MOMOT
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Odszukanie rekordu
Przeszukiwanie sekwencyjne
Przeszukiwanie dychotomiczne
Przeszukiwanie z użyciem funkcji mieszającej
Analiza efektywności funkcji mieszającej
Ponieważ liczba prób przy rozmieszczaniu jest taka sama jak przy
odszukiwaniu, to średnia liczba prób potrzebnych do znalezienia
losowego klucza w tablicy wypełnionej M elementami:
M
1
1 X
En+1 = − log2 (1 − α),
L=
M n=1
α
gdzie
M
N +1
jest ilorazem liczby zajętych i dostępnych adresów – współczynnikiem
N
wypełnienia. Gdy tablica jest pusta, to α = 0, gdy pełna α = N+1
.
α=
dr inż. Alina MOMOT
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Odszukanie rekordu
Przeszukiwanie sekwencyjne
Przeszukiwanie dychotomiczne
Przeszukiwanie z użyciem funkcji mieszającej
Analiza efektywności funkcji mieszającej - wnioski
Ze względu na efektywność zaleca się aby pojemność tablicy mieszająca
była 10% - 20% większa od przewidywanej liczby danych.
dr inż. Alina MOMOT
Synchronizacja procesów
Plan wykładu
Informatyka
Bazy danych
Przeszukiwanie tablic
Odszukanie rekordu
Przeszukiwanie sekwencyjne
Przeszukiwanie dychotomiczne
Przeszukiwanie z użyciem funkcji mieszającej
Wady zastosowania funkcji mieszającej
Teoretycznie wyszukiwanie elementu ma złożoność czasową O(1),
ale w przypadku pesymistycznym wynosi O(N).
Obliczanie wartości dobrej funkcji mieszającej może być bardzo
kosztowne.
Zastosowanie tablicy mieszającej dla zbyt małej liczby elementów
może być wolniejsze niż zastosowanie zwykłej tablicy przeszukiwanej
sekwencyjnie1 .
1
ze względu na wykorzystanie pamięci podręcznej, która przyspiesza odwołania do
komórek pamięci operacyjnej gdy są one zgrupowane blisko siebie
dr inż. Alina MOMOT
Synchronizacja procesów