Magdalena Gawrońska

Magdalena Gawrońska
nr albumu 135743
Sprawozdanie z ćwiczeń laboratoryjnych
z fizyki
Wyznaczanie ciepła właściwego ciał
stałych metodą kalorymetryczną.
Prowadzący ćwiczenia:
dr W. Kumala
1. Wstęp.
Mierzeniem ilości ciepła zajmuje się dział nauki o cieple zwany kalorymetrią.
Kalorymetria opiera się na kilku prostych zasadach, które można wyrazić następująco:
1. Ilość ciepła Q1 oddana przez ciało jest równa ilości ciepła Q2 pobranej przez jego
otoczenie (przez ciała, które je otaczają).
2. Ilość ciepła pobrana przez ciało podczas ogrzewania jest równa ilości ciepła oddanej
podczas stygnięcia w tym samym zakresie temperatur, jeżeli w odwrotnym porządku
przechodzi ono przez te same stany pośrednie.
3. Ilość ciepła Q pobrana przez ciało w procesie ogrzewania (lub oddana w procesie
chłodzenia) jest proporcjonalna do iloczynu jego masy oraz powstałego (dodatniego lub
ujemnego) przyrostu temperatury t
Q=m c t
gdzie współczynnik proporcjonalności c nazywamy jego ciepłem właściwym. W przypadkach
1. i 2. przyjmujemy, że ciała przyjmujące lub oddające ciepło nie wykonują równocześnie
pracy, ani też że nie jest ona na nich wykonywana.
Rys. 1. Kalorymetr wodny.
Nie istnieje kalorymetr izolujący doskonale. Zawsze pewne nieznane ilości ciepła nie
dają się rachunkowo uwzględnić, np. nieznane straty powstają w momencie przenoszenia
ciała z ogrzewacza do naczynia kalorymetrycznego, na skutek nieuniknionego parowania i
konwekcji, (pomiędzy naczyniem K i płaszczem B jest powietrze) itp. Najbliższym idealnego
byłby kalorymetr o płaszczu próżniowym (naczynie Dewara – termos). Te czynniki
powodują, że wynik badania jest obarczony na ogół większym błędem, niż to wynika z
formalnej analizy przeprowadzonej na gruncie teorii błędów.
2. Wyniki i obliczenia.
A) Masy badanych ciał.
m1 = 66,2  0,002 [g]
m2 = 29,5  0,002 [g]
m3 = 18,4  0,002 [g]
B) Masa naczynia kalorymetrycznego i mieszadełka.
mm = 7,6  0,002 [g]
mk = 150,7  0,002 [g]
C) Masa wody dla poszczególnych pomiarów.
mw= mkw - mk
(gdzie mkw –naczynie z wodą)
mw1 =241,1 – 150,7 = 90,4  0,002 [g]
mw2 =241,1 – 150,7 = 90,4  0,002 [g]
mw3 =234,0 – 150,7 = 83,3  0,002 [g]
D) Temperatury początkowe ciał.
TC1 = 95,4  C
TC2 = 96,2  C
TC3 = 95,0  C
E) Temperatura początkowa i końcowa w procesie wymiany ciepła odczytana z
wykresów.
TP1 = 16,2  C
TK1 = 21,0  C
TP2 = 17,6 C
TK2 = 21,6  C
TP3 = 16,7  C
TK3 = 19,6  C
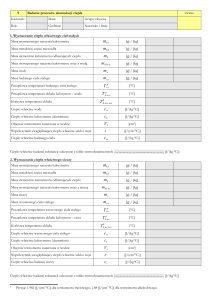
F) Wielkości stałe.
Ciepło właściwe wody: cw =4185  8 [J/kg K]
Ciepło właściwe kalorymetru mosiężnego: ck =390  5 [J/kg K]
Ciepło właściwe mieszadełka cm = 897  5 [J/kg K]
G) Wyznaczone wielkość wynoszą:
c1 = 433  23 [J/kg C]
c2 = 807 15 [J/kg C]
c3 = 926  58 [J/kg C]
-Przykładowe obliczenia dla ciała 1:
cx 
c1 
-
cw  mw  ck  mk  cm  mm   TK  TP 
mc  TC  TK 
4185  0,0904  390  0,1507  897  0,0076  21,0  16,2  433
0,0662  95,4  21,0
 J 
 kg  C 


Niepewność pomiarów:
(TK- TP) = 0C + (TK- TP)0,9% + 0,2C
(TC- TP) = 1C + TC  0,9% + TP  0,9% + 0,2C
 c  mw  mw  c w  ck  mk  mk  ck  mm  c m TK  TP  mc TC  TK  
  c x
c x   w









c

m

c

m

c

m
T

T
m
T

T
w
w
k
k
m
m
K
P
c
C
K


 4185  0,000002  0,0904  8  390  0,000002  0,1507  5  0,0076  5 0,2432 0,000002 2,2 
  433 
c1  



4185  0,0904  390  0,1583  897  0,0076
4,8
0,0662
74,4 

 23
3. Wnioski.
Metoda kalorymetryczna pozwala na wyznaczenie ciepła właściwego z dokładnością do
ok. 5%. Błąd ten nie uwzględnia jednak wielu czynników wypływających w trakcie
pomiarów takie jak wymiana ciepła z otoczeniem podczas przenoszenia ciała do kalorymetru
czy ciepło wyprowadzane przez mieszadełko. Niedokładne mieszanie może mieć również
spory wpływ na otrzymane wyniki. Z rachunku błędów wynika, że największą niedokładność
wprowadza błąd ciepła właściwego wody, błąd pomiaru jej temperatury, oraz błąd pomiaru
temperatury ciała. Źródłem nieznanego, z powodu strat powstałych w momencie przenoszenia
ciała z ogrzewacza do naczynia kalorymetrycznego, na skutek parowania i konwekcji, błędu
jest również to, że nie można dokładnie wyznaczyć temperatur początkowej TP i końcowej TK
w procesie wymiany ciepła. Aby ten błąd zminimalizować wprowadza się graficzny sposób
określenia T P i TK .
Porównując otrzymane wyniki z wartościami tablicowymi można przypuszczać,
iż badane ciała były wykonane z następujących materiałów:
1- mosiądz
2- miedź
3- aluminium
Zestawienie wyników:
c1 = 433  23 [J/kg C]
c2 = 807 15 [J/kg C]
c3 = 926  58 [J/kg C]