Masz do dyspozycji:

LII OLIMPIADA FIZYCZNA
2002/2003
Zawody III stopnia
Masz do dyspozycji:






żarówkę z włóknem wolframowym, o napięciu znamionowym 2,2 V,
oscyloskop,
zasilacz napięcia stałego, regulowanego w zakresie 03 V
opornik o oporności 1 ,
przewody elektryczne,
papier milimetrowy.
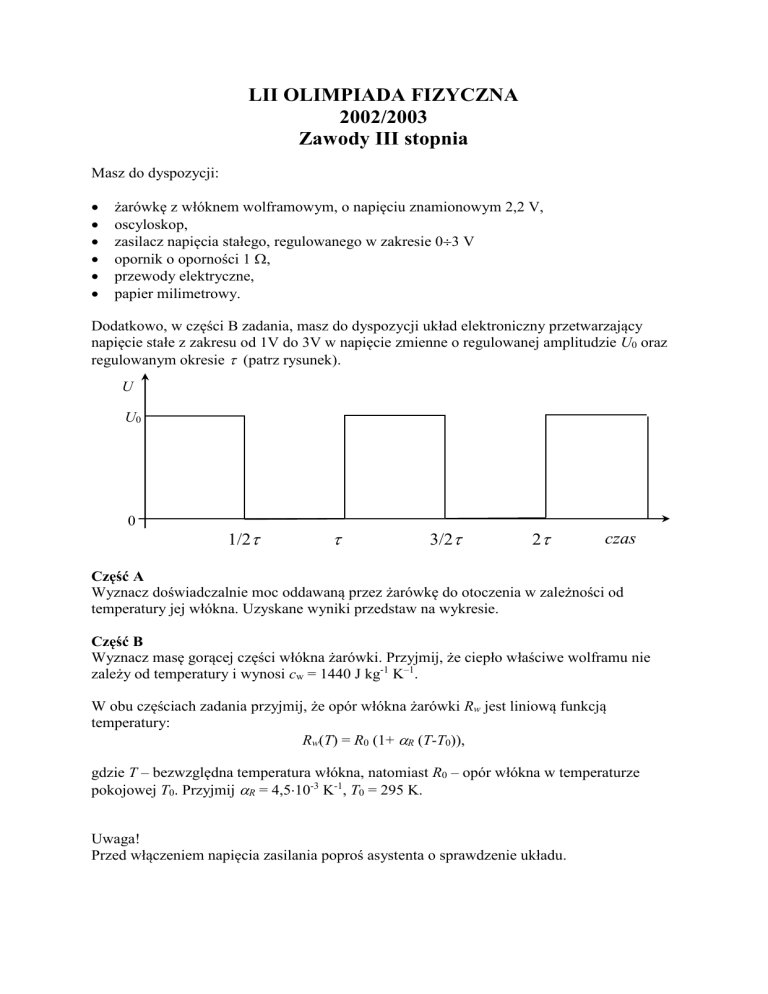
Dodatkowo, w części B zadania, masz do dyspozycji układ elektroniczny przetwarzający
napięcie stałe z zakresu od 1V do 3V w napięcie zmienne o regulowanej amplitudzie U0 oraz
regulowanym okresie  (patrz rysunek).
U
U0
0
1/2

3/2
2
czas
Część A
Wyznacz doświadczalnie moc oddawaną przez żarówkę do otoczenia w zależności od
temperatury jej włókna. Uzyskane wyniki przedstaw na wykresie.
Część B
Wyznacz masę gorącej części włókna żarówki. Przyjmij, że ciepło właściwe wolframu nie
zależy od temperatury i wynosi cw = 1440 J kg-1 K–1.
W obu częściach zadania przyjmij, że opór włókna żarówki Rw jest liniową funkcją
temperatury:
Rw(T) = R0 (1+ R (T-T0)),
gdzie T – bezwzględna temperatura włókna, natomiast R0 – opór włókna w temperaturze
pokojowej T0. Przyjmij R = 4,510-3 K-1, T0 = 295 K.
Uwaga!
Przed włączeniem napięcia zasilania poproś asystenta o sprawdzenie układu.
Część teoretyczna
Część A
Wyznaczenie zależności mocy emitowanej przez żarówkę od temperatury jej włókna można
wykonać w układzie, którego schemat elektryczny przedstawiono schematycznie na rys. 1.
I
A
Uz
Zasilacz
+
U0
B
UR
R = 1
M
Oscyloskop
Rys.1
W układzie tym oscyloskop wykorzystany jest w roli woltomierza napięcia stałego.
Podłączając go miedzy punkty MB oraz MA układu możemy wyznaczyć prąd I = UR/R oraz
napięcie Uz=U0-UR. Pozwala to wyznaczyć moc Ps =( U0-UR)UR/R dostarczaną do żarówki
oraz opór jej włókna Rw = R ( U0-UR)/UR. Dla określenia temperatury włókna konieczne jest
wyznaczenie jego oporności R0 odpowiadającej znanej temperaturze, np. temperaturze
pokojowej. W tym celu należy wykonać wykres zależności mocy Ps od oporu włókna Rw.
Ekstrapolując wyniki do granicy Ps  0 można otrzymać wartość R0 odpowiadającą
temperaturze panującej w sali, w której wykonywane są pomiary. Znając opór włókna można
będzie wyznaczyć jego temperaturę, co umożliwi wykonanie wykresu zależności mocy
oddawanej przez żarówkę do otoczenia od temperatury jej włókna.
Część B
Zasilając żarówkę z napięciem prostokątnym można w sposób cykliczny, zmieniać jej
temperaturę. Odpowiednie pomiary można wykonać w układzie przedstawionym
schematycznie na rys. 2.
I
A
G
Uz
U0
B
U
R
Rys. 2
R = 1
M
Oscylosko
p
W momencie, gdy między punktami MA napięcie osiąga pewną niezerową wartość U0 przez
żarówkę zaczyna płynąć prąd i w miarę upływu czasu temperatura jej włókna wzrasta do
wartości Tm1 (Rys.3). W tym czasie wzrasta również opór włókna, natomiast wartość prądu
płynącego przez żarówkę maleje. W chwili, gdy napięcie zasilające układ spada do zera,
temperatura włókna zaczyna maleć, osiągając minimalną wartość T1. Wtedy napięcie
zasilania ponownie wzrasta i cykl ogrzewania i stygnięcia włókna powtarza się. Zmieniając
wartość napięcia U0 można regulować zarówno zakres jak i tempo zmian temperatury włókna.
Na rys. 3. przedstawiono (linią przerywaną) oczekiwane zmiany temperatury włókna dla
napięcia U02<U0.
U
U0
0
UR
UR0
t
URS
t
T
Tm1
T1
Tm2
T2
t0
t1
t2
t3
t5
t6
t
Rys. 3
Szybkość zmian temperatury włókna zależy od szybkości dostarczania do niego energii, jego
masy m oraz ciepła właściwego cw . Załóżmy, że w krótkim przedziale czasu t dostarczymy
do włókna pewną porcję energie. Część tej energii zostanie spożytkowana na wzrost
temperatury włókna, a część zostanie oddana do otoczenia. Jeśli przyjmiemy, że dostarczając
przez czas t do włókna moc P spowodowaliśmy wzrost jego temperatury o T to bilans
energii dostarczonej i oddanej otoczeniu można zapisać w postaci:
P-Ps = mcwT/t,
.
(1)
gdzie Ps – moc strat. Ponieważ zależność mocy Ps od temperatury wyznaczona zostanie w
części A zadania to, zgodnie ze wzorem (1), dla znalezienia masy włókna pozostaje
wyznaczyć szybkość zmian temperatury włókna przy dostarczaniu mu mocy P-Ps.
Zmianę temperatury włókna T można wyznaczyć badając zmianę jego oporu Rw:
T
1 Rw

.
(2)
t R02 t
gdzie R0 – opór włókna w temperaturze pokojowej.
Wyrażając opór włókna przez napięcia mierzone między punktami MA (U0) oraz MB (UR)
dostajemy:
U
U R
T
  20 2
t
R0 U R t
(3)
Jeśli zmianę temperatury włókna mierzyć będziemy tuż po pojawieniu się napięcia na
żarówce, to odpowiadająca je mocy dostarczanej do włókna wyniesie:
U R 0 (U 0  U R 0 )
,
R
gdzie UR0 – napięcie na oporniku R na początku cyklu ogrzewania włókna.
P  I (U 0  U R 0 ) 
(7)
Część doświadczalna
Część A
Zmieniając napięcie U0 miedzy punktami MB obwodu przedstawionego na rys.1, mierzymy
opowiadające mu napięcie UR na oporniku szeregowo połączonym z żarówką. Obraz na
oscyloskopie tworzy pozioma linię. Jej odległość od poziomu odpowiadającego napięciu
zerowemu odpowiada mierzonemu napięciu.
Uzyskaną zależność oporu żarówki od temperatury przedstawiono na rys. 4.
1.0
Ps
0.8
Ps (W)
0.6
0.4
Ps=0,030* R-0,027
R0 = 0,93 
0.2
0.0
0
2
4
6
8
10
12
R ()
Rys. 4
Wynika z niego, że dla małych wartości oporu włókna moc oddawana przez żarówkę do
otoczenia jest jego liniową funkcją. Korzystając z wykresu, można zatem łatwo odczytać opór
włókna odpowiadający oporowi włókna w temperaturze pokojowej (T0 = 293 K) R0 =
0,950,05 . Pozwala to wykonać wykres zależności mocy oddawanej przez żarówkę do
otoczenia od temperatury jego włókna(rys. 5).
0.8
0.7
0.6
Ps (W)
0.5
0.4
0.3
0.2
0.1
0.0
0
500
1000
1500
2000
T(K)
Rys. 5 Zależność mocy oddawanej przez żarówkę do otoczenia od temperatury jej włókna.
Część B
Zestawiamy układ doświadczalny zgodnie ze schematem przedstawionym na Rys. 1.
Łączymy oscyloskop z punktami BM obwodu. Odpowiednio dobierając podstawę czasu oraz
wzmocnienie, odczytujemy z oscyloskopu wartość napięcia UR0 oraz szybkość zmian napięcia
UR, tzn. UR/t. Posługujemy się przy tym podziałką z ekranu oscyloskopu (rys 3). Podobnie
odczytujemy napięcie URS. Napięcie U0 wyznaczamy podłączając oscyloskop miedzy punkty
AM obwodu (rys. 1).
UR0
t
UR
Rys. 3
Korzystając ze wzorów wyprowadzonych w części teoretycznej wyznaczamy moc P
pobieraną przez żarówkę w początkowym okresie rozgrzewania włókna oraz straty mocy Ps.
Wyniki otrzymane dla różnych temperatur włókna przedstawiono na rys. 6.
0.8
Ps
P
0.7
0.6
Moc (w)
0.5
0.4
0.3
0.2
0.1
0.0
400
600
800
1000
1200
1400
Temperatura (K)
Rys. 6
Z wykresów przedstawionych na rys. 6 wynika, że straty mocy Ps są znacznie mniejsze od
mocy P potrzebnej dla wywołania zmiany temperatury włókna. W interesującym obszarze
temperatur włókna, zależność mocy strat Ps od temperatury można opisać zależnością
liniową. Dzięki temu, można łatwo wyznaczyć interesującą nas różnicę mocy P- Ps
odpowiadającą danej temperaturze włókna. Zależność różnicy mocy P – Ps od szybkości
zmian temperatury włókna T/t przedstawiono na rys. 7.
0.8
b = 0.026(5)
0.7
0.6
P-Ps (W)
0.5
0.4
0.3
0.2
0.1
0.0
0
10
20
30
40
50
60
T / t (K/ms)
Rys. 7
Do uzyskanych danych doświadczalnych dopasowano prostą, uzyskując parametr nachylenia
b = mcw= (265)10-3 J. Biorąc pod uwagę wartość ciepła właściwego wolframu
cw = 1440 J kg-1K–1, otrzymano masę włókna żarówki m = 184g. Wynik ten jest zgodny z
wartością uzyskaną z bezpośredniego ważenia włókna usuniętego z badanej żarówki.
Punktacja
Część A
a) zestawienie układu doświadczalnego i wykonanie pomiarów mocy
oddawanej przez żarówkę do otoczenia w zależności od temperatury włókna
b) wyznaczenie oporu R0
c) wykonanie wykresu zależności Ps (T)
do 2pkt.
do 2pkt.
do 2 pkt.
Część B
a) pomysł rozwiązania, wyprowadzenie wzorów
b) skorzystanie z bilansu energii dla włókna
c) wykonanie pomiarów umożliwiających wyznaczenie masy włókna
d) poprawny wynik
do 4pkt.
do 4pkt.
do 4 pkt.
do 2 pkt.