Początki Wszechświata
Krystyna Wosińska
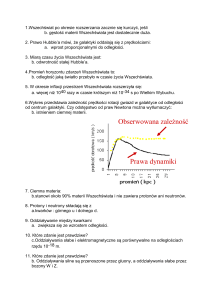
Dane obserwacyjne
Odkrycie Hubble’a w 1929 r.
v = H·r
Promieniowanie tła w 1964 r.
(Arno Penzias i Robert Wilson).
Skład Wszechświata: jakie
cząstki i w jakim stosunku
ilościowym tworzą Wszechświat.
Podstawy teoretyczne
Ogólna teoria względności (1917)
Równanie Friedmana opisujące globalną ewolucję Wszechświata
2
8
G
kc
2
H
2
3
R
H - stała Hubble’a
(v = H·R)
G – stała grawitacji
- gęstość materii Wszechświata
c – prędkość światła
k – zakrzywienie przestrzeni
R – czynnik skali – mierzy średnie oddalenie dwóch punktów
(np. gromad galaktyk)
= / k
Ten parametr wyznacza przyszłość
Wszechświata
<1
=1
>1
W miarę rozszerzania się Wszechświata maleje zarówno gęstość
rzeczywista, jak i krytyczna. Stosunek tych gęstości jest stały.
Jeśli wyznaczymy , odkryjemy przyszłość Wszechświata
Einstein dodał do równania stałą kosmologiczną , aby „ratować”
płaski i statyczny Wszechświat.
2
8
G
kc
2
H
2
3
R
3
- reprezentuje siłę odpychającą, równoważącą przyciąganie
grawitacyjne – dzięki niej pojawia się rozwiązanie równania opisujące
statyczny Wszechświat.
W 1922 r. Aleksander Friedman znalazł wszystkie rozwiązania
równania i wykazał, że nawet dodanie stałej kosmologicznej nie
zapewni stałości Wszechświata.
Einstein nazwał dodanie stałej kosmologicznej swoją największą
pomyłką, jednak obecnie wcale nie jest oczywiste, że wynosi ona
zero!
Era Plancka
10-44 s
Temperatura 1032 K
Dwie cząstki punktowe o masach równych masie Plancka
i oddalone o długość Plancka:
grawitacyjna
energia potencjalna
GM P2
M Pc2
lP
Masa Plancka:
c
MP
1,22 1019 GeV
G
masa spoczynkowa
Długość Plancka:
lP
1,66 10 33 cm
MPc
Era Plancka
Aby opisać Wszechświat w erze Plancka,
trzeba połączyć teorię grawitacji z
mechaniką kwantową.
Mechanika kwantowa
Obiekty kwantowe (kwarki, atomy, ...) mogą istnieć w
różnych stanach.
Przestrzenią tych stanów jest przestrzeń Hilberta
Przestrzeń Hilberta – liniowa przestrzeń wektorowa
Każdy wektor (stan układu) można przedstawić jako
kombinację liniową innych wektorów.
Układ może znajdować się w superpozycji dwu lub więcej stanów
Świat mechaniki kwantowej jest światem probabilistycznym
Mechanika kwantowa
Obserwable – wielkości mierzalne (np. położenie, pęd)
Obserwabli odpowiada operator działający na przestrzeni Hilberta
A :
Pomiar zaburza stan obiektu – ze
stanu przeprowadza go w stan
Działanie operatora A na wektor stanu opisuje równanie,
którego rozwiązaniem są wartości własne (wyniki pomiaru)
Rozwiązania skwantowane – wyniki pomiarów
mogą przybierać tylko wartości dyskretne
Teoria grawitacji
Równania pola grawitacyjnego określające zakrzywienie
czasoprzestrzeni są silnie nieliniowe
Pole dwu ciał nie jest sumą pól poszczególnych pól
Geometrodynamika
Wheelera
Stany Wszechświata
zakreślają krzywą w
przestrzeni wszystkich
możliwych stanów – w
superprzestrzeni.
przestrzeń
Próby skwantowania grawitacji
Stan Wszechświata:
w chwili t1
t1
w chwili t2
t2 czas
DeWitt zaproponował, aby na superprzestrzeni
zdefiniować funkcje falowe
Wartość funkcji falowej w danym punkcie
superprzestrzeni, czyli w danym stanie Wszechświata
– prawdopodobieństwo urzeczywistnienia tego stanu.
Próby skwantowania grawitacji
Równanie Wheelera-DeWitta – równanie na funkcje falowe
Wszechświata w superprzestrzeni.
Niespodzianka: funkcje falowe Wszechświata
nie zależą w tym równaniu od czasu!
W kwantowo-grawitacyjnym reżimie czas nie może być zewnętrznym
parametrem, który numeruje następujące po sobie stany.
Czas staje się elementem kwantowej gry –
ma charakter probabilistyczny.
Stany Wszechświata nie następują po sobie w sposób konieczny; istnieje
jedynie określone prawdopodobieństwo układania się poszczególnych
stanów w następujące po sobie ciągi. I dopiero przy przejściu przez próg
Plancka prawdopodobieństwa dążą do jedności i wyłania się
deterministyczna ewolucja z czasem jako zewnętrznym parametrem.
Michał Heller, „Kosmologia kwantowa”
Model Standardowy
Do chwili obecnej odkryto około dwieście cząstek (z których większość
nie jest cząstkami elementarnymi).
Model Standardowy – teoria opisująca wszystkie cząstki i oddziaływania
między nimi za pomocą:
•6 kwarków
•6 leptonów
•cząstek przenoszących oddziaływania
Każdej cząstce odpowiada
antycząstka
Odziaływanie elektromagnetyczne
•Działa na ładunki elektryczne
•Odpowiedzialne za wiązania chemiczne
•Nośnik – foton ()
•Zasięg – nieskończony
Odziaływanie silne
•Działa na ładunki kolorowe
•Odpowiedzialne za wiązanie kwarków w barionach
•Nośniki – gluony
•Zasięg – 10-15 m (odległość typowa dla kwarków w
nukleonie)
Uwięzienie kwarków
•Oddziaływanie między kwarkami rośnie wraz z odległością.
•Próba rozdzielenia kwarków prowadzi do wytworzenia nowej pary
kwark-antykwark (jest to proces korzystniejszy energetycznie).
mezon D-
mezon D+
mezon c
E mc
2
Zamiana energii na masę
Oddziaływanie słabe
•Odpowiedzialne za rozpad ciężkich kwarków i leptonów na lżejsze
kwarki i leptony (zmiana zapachu).
•Cząstki przenoszące oddziaływanie słabe to bozony: W+, W- i Z0.
Masy W+, W- i Z0 duże (~80 GeV)
Zasięg mały
Oddziaływanie słabe i elektromagnetyczne opisuje
jednolita teoria oddziaływań elektrosłabych.
Oddziaływania elektrosłabe
Małe odległości (10-18 m) wielkie energie
Oddziaływania słabe i elektromagnetyczne
porównywalne.
Większe odległości (3•10-17 m)
Oddziaływanie słabe jest 10-4 razy mniejsze niż
elektromagnetyczne
Słaby rozpad
e
W
e
e
e
e
e
W rozpadzie pośredniczy
bozon W-
Oddziaływanie grawitacyjne
•Działa na każde ciało
•Odpowiedzialne za istnienie planet, gwiazd,
galaktyk...
•Nośnik (hipotetyczny) – grawiton?
•Zasięg – nieskończony
Brak teorii, która wiąże oddziaływanie grawitacyjne z
innymi rodzajami oddziaływań – jeden z głównych
nierozwiązanych problemów kosmologii.
Oddziaływania
elektrosłabe
grawit.
grawiton
(?)
γ
W+
WZo
silne (kolorowe)
masa
[GeV]
ładunek
0
80.4
80.4
91.2
0
+1
-1
0
ggluon
masa
[GeV]
ładunek
0
0
superoktet SU(3)
8 stanów koloru
Literatura:
•http://chall.ifj.edu.pl/przygodazczastkami/frameless/index.html
•http://www.wiw.pl/fizyka/boskaczastka/
•L. Lederman „Boska cząstka”
Unifikacja oddziaływań
Przy wielkich energiach oddziaływania słabe i
elektromagnetyczne są porównywalne –
oddziaływania elektrosłabe.
Jeszcze większe
energie zrównanie
oddziaływań
elektrosłabych i
silnych
TOE – Theory Of Everything
nie istnieje!
GUT – Grand Unified Theory nie
potwierdzona doświadczalnie!
Teoria Wielkiej Unifikacji
GUT – Grand Unified Theory
Modele supersymetryczne (SUSY)
Tuż po erze Plancka przy temperaturach powyżej 1028 K (EGUT = 1016 GeV)
Wszechświat wypełniała mieszanina kwarków, leptonów oraz cząstek
przenoszących oddziaływania — fotonów, bozonów W i Z oraz gluonów.
Nierozróżnialne oddziaływania (nośniki) są w równowadze z
materią i antymaterią.
Przykład:
W W qq
Oddziaływania elektro-magnetyczne, słabe i silne są
nierozróżnialne.
GUT wymaga istnienia dodatkowych nośników
oddziaływań – 12 bozonów (i antybozonów) X (X )
Problemy do wyjaśnienia...
Cząstki i antycząstki pojawiają się i anihilują zawsze
parami. Obowiązuje prawo zachowania liczby barionowej i
leptonowej.
Dlaczego więc we Wszechświecie nie ma równej
ilości materii i antymaterii?
Drugim ważnym faktem obserwacyjnym jest
dramatyczna przewaga ilości fotonów (tła reliktowego)
nad ilością barionów η = nb/nγ ≤ 10-9
Jak to wytłumaczyć?
Bozony X i Y
•Ładunek = 1/3 i 4/3
•Ładunek kolorowy R, G, B
Leptokwarki
•Ładunek leptonowy
•Masa 1016 GeV
Bozony X w oddziaływaniach z kwarkami (q) i leptonami (l)
mogą powodować przemiany kwarku w antykwark (i odwrotnie)
oraz kwarku w lepton (i odwrotnie).
”Przy temperaturach GUT (1028 K) symetria i prostota osiągają
poziom, na którym istnieje tylko jeden rodzaj materii (lepto-kwark?)
i jedno oddziaływanie z całym wachlarzem cząstek-nośników oraz... no
tak, dynda tam jeszcze z boku grawitacja.” - Leon Lederman
Bozony X
Rozpady bozonów X:
X q q
X qq
X ql
X ql
Bozony X
Przy temperaturach T > 1028 K pary X + anty-X powstają i anihilują
zupełnie symetrycznie.
Gdy jednak temperatura spada poniżej 1027 K, kreacja i anihilacja par
staje się coraz mniej prawdopodobna, wzrasta zaś szansa
spontanicznego rozpadu.
Prawdopodobieństwa różnych kanałów rozpadów mogą być różne:
X
X
p1
1-p1
q q
ql
Jeśli p1 = p2, to po rozpadach
pozostaną równe ilości
kwarków i antykwarków oraz
leptonów i antyleptonów.
X
X
p2
1-p2
qq
ql
Jeśli p1 p2, to pozostanie
pewna nadwyżka materii nad
antymaterią.
Bozony X
Różnica p1 i p2 rzędu 10-9 wystarczy do wyjaśnienia
obserwowanego obecnie stosunku ilości barionów do
fotonów we Wszechświecie.
Jak wielka była nadwyżka
materii nad antymaterią?
Na 30 mln antykwarków
przypadało (30 mln + 1) kwarków
Czas życia protonu
Konsekwencją GUT jest
nietrwałość protonu.
Doświadczalne potwierdzenie:
Rozpad p na neutralny pion
i pozyton w czasie 1030 lat
Wiek Wszechświata 1010 lat
Prawdopodobieństwo rozpadu
jednego protonu w ciągu roku
wynosi 10–30.
Zamiast tego możemy obserwować wiele protonów.
W 10 000 ton wody - około 1033 protonów
W ciągu roku około tysiąca protonów powinno ulec
rozpadowi.
Czas życia protonu
Eksperymenty, które mają wykryć rozpad protonu rozpoczęto w
latach 70 w podziemnych laboratoriach (tło od mionów z
promieniowania kosmicznego)
•Superkamiokande (Japonia) w kopalni:
Ogromny, przezroczysty walec z czystą wodą (około 50 000 ton) –
otacza go 11 000 czułych fotopowielaczy.
Inne eksperymenty:
•Irvine-Michigen-Brookhaven
•Soudan 2
•Frejus
•Nusex
Wynik: nie zaobserwowano rozpadu protonu!
Wniosek: czas życia protonu > 1032 lat
Teoria inflacji
Problemy, które trzeba wyjaśnić:
• Problem horyzontu
• Problem monopoli magnetycznych
• Problem płaskości Wszechświata
Problem horyzontu
Niezależnie od jakości teleskopów, nie możemy obserwować dowolnie
odległych obiektów. Największa odległość, w której światło zdążyło
dotrzeć do obserwatora w czasie istnienia Wszechświata wynosi :
R T c
Gdzie: T – wiek Wszechświata, c – prędkość światła
?
?
13,7 mld lat świetlnych
3·1027 cm
?
Horyzont można też zdefiniować
podstawiając do prawa Hubble’a
maksymalną prędkość ucieczki
galaktyk równą prędkości
światła:
1
c H R R c T c
H
Problem horyzontu
Obserwujemy we wszystkich kierunkach wysoką jednorodność
Wszechświata, zarówno w skali wielkoskalowej (galaktyki, gromady
galaktyk), jak i promieniowania mikrofalowego, którego natężenie i
temperatura są identyczne we wszystkich kierunkach z dokładnością do
1/1000.
A
Nasza galaktyka
B
Punkty A i B nie mogły ze sobą
oddziaływać od początku
istnienia Wszechświata, więc
skąd ta jednorodność...?
Problem horyzontu
T = 3·1028 K
T = 3K
Ekspansja o
czynnik 1028
Obecny horyzont
zdarzeń
Horyzont zdarzeń
3·10-25 cm
Wiek = 10-35 s
Wiek = 1017 s
W wieku 10-35 s Wszechświat składał się z ogromnej liczby niezależnych,
rozdzielonych obszarów?? Sprzeczność z obserwowaną
jednorodnością!
Problem monopoli magnetycznych
P. Dirac (w 1931): dopuszczalne jest istnienie monopoli
magnetycznych o wartości:
4c
g n
2e
Teorie Wielkiej Unifikacji przewidują powstanie ogromnej liczby monopoli
magnetycznych – cząstek o masach 1016 razy większych niż masa
protonu. Z obliczeń wynika, że monopoli byłoby teraz tysiące razy więcej
niż protonów czy neutronów.
Jednak monopole nie są obserwowane!
Problem płaskości Wszechświata
Względna gęstość materii we Wszechświecie:
k
Dane obserwacyjne i teoretyczne przewidywania ograniczają
dzisiejszą wartość do przedziału od 0,1 do 2.
Początkowa wartość była
bardzo niestabilna i
jakiekolwiek odchylenie od
wartości 1 szybko
wzrosłoby w czasie.
Problem płaskości Wszechświata
Aby dzisiejsza mieściła się w żądanym przedziale,
początkowa jej wartość
musiała być równa jedności z
dokładnością większą niż 1 na 10-15.
Początkowy Wszechświat był bardzo płaski!
Warunki początkowe Wszechświata zostały dostrojone z
wielką precyzją, aby mógł powstać dzisiejszy świat. Małe
wahanie na początku ewolucji Wszechświata sprawiłoby, że
zapadłby się w krótkim czasie lub materia tak szybko by się
oddalała, że nie powstałyby gwiazdy i planety.
Skąd to wykalibrowanie warunków początkowych?
Wszechświat inflacyjny
Po upływie czasu Plancka Wszechświat o temperaturze 1014 GeV
podlegał Wielkiej Unifikacji Oddziaływań (oddziaływania silne, słabe i
elektromagnetyczne nie różniły się).
Wszechświat zawierał obszary „fałszywej próżni” wypełnione ogromną
energią – ewolucja była kontrolowana przez oddziaływania ze skalarnym
polem „inflatonu” ).
„Fałszywa próżnia” to obszar o zadziwiających własnościach:
•jej gęstość nie zmienia się wraz z rozszerzaniem się
•wytwarza ona ujemne ciśnienie
Z ciśnieniem jako formą energii związana jest grawitacja.
Ujemne ciśnienie prowadzi do odpychającej siły grawitacyjnej –
odpowiada tej sytuacji niezerowa stała kosmologiczna .
Nastąpiła ekspansja!
Wszechświat inflacyjny
Wzór kosmologiczny:
2
8
G
kc
2
H
2
3
R
3
Te człony maleją
gwałtownie podczas
rozszerzania
2
Zostaje:
r
gdzie:
3
r
Rozwiązanie równania:
r
H
r
r
r ( t ) exp
t
3
Ekspansja wykładnicza!
r
3
Wszechświat inflacyjny
Wykładnicza ekspansja zakończyła się w chwili 10-34 s po Wielkim
Wybuchu.
Jak powiększył się w tym czasie Wszechświat?
r ( t ) exp
t exp H t )
3
Załóżmy, że inflacja zaczęła się w chwili T = H-1 = 10-36 s
rkon
expH t kon t pocz e 99 1043
rpocz
Wszechświat powiększył się w ułamku sekundy do
rozmiarów wielokrotnie przekraczających wszystko co
możemy obserwować!
Wszechświat inflacyjny
Inflacja zakończyła się przejściem fazowem – „fałszywa próżnia”
zamieniła się w próżnię prawdziwą wypełnioną cząstkami.
Towarzyszyło temu wyzwolenie ogromnej energii, która ponownie
„podgrzała” Wszechświat
Analogia:
Uwolniona energia
woda
lód
Podczas przejścia fazowego uwalnia się energia
Wszechświat inflacyjny
Po zakończeniu okresu inflacji Wszechświat rozszerza się dalej ze
stałą kosmologiczną równą zeru.
Teorię inflacji zaproponował w 1981 roku Alan Guth teoretyk fizyki
cząstek elementarnych zajmujący się Teorią Wielkiej Unifikacji.
Wszechświat inflacyjny
Rozwiązanie problemu jednorodności Wszechświata:
3·10-25 cm
Obserwowalny Wszechświat powstał z bardzo małego jednorodnego
obszaru.
Wszechświat inflacyjny
Rozwiązanie problemu monopoli:
Na skutek inflacji gęstość monopoli, jeśli istniały,
spadła do infinitezymalnie małej wartości.
Wszechświat inflacyjny
Rozwiązanie problemu płaskości Wszechświata:
Z równania Friedmana dla Wszechświata inflacyjnego
można otrzymać związek:
4
( t ) 1 exp
t
3
Oznacza on, że szybko dąży do jedności
Obecny Wszechświat jest płaski!
Historia Wszechświata
10-34 s
Temperatura 1027 K
Materia w postaci plazmy kwarkowo-gluonowej.
Wszechświat wypełniają swobodne kwarki, gluony, leptony,
bozony W i Z, fotony, które oddziaływują ze sobą.
Oddziaływanie silne oddziela się od oddziaływania elektrosłabego.
Od tej chwili oddziaływania te znacznie różnią się wielkością.
Era hadronowa
10-9 s
Temperatura 1015 K (250 GeV)
Kwarki łączą w hadrony, które są cząstkami relatywistycznymi.
Kreacja i anihilacja par hadronów jest w równowadze.
Hadrony, leptony i nośniki oddziaływań (fotony,
bozony W i Z) są w równowadze termodynamicznej.
Oddziaływanie słabe oddziela się od elektromagnetycznego.
Era hadronowa
W miarę ekspansji i stygnięcia
Wszechświata przestają być
produkowane najcięższe i
nietrwałe hadrony.
Przy 80 GeV przestają być też
produkowane bozony W i Z
Przy T < 1012 K także protony
i neutrony przestają być
cząstkami relatywistycznymi.
Jednocześnie zaczyna się
przewaga procesów
anihilacji tych cząstek nad
kreacją par.
Era hadronowa
Era hadronowa zbliża się do końca po ok. 10-4 s,
przechodząc w erę leptonową.
Prawie wszystkie protony i
neutrony anihilują (dodając
fotony do tła promieniowania).
Pozostaje nadwyżka materii
nad antymaterią.
Czas trwania ery hadronowej (10-4 s ) wydaje się być
znikomo krótki. Jednak czas życia większości hadronów i
skala czasowa oddziaływań silnych to ok. 10-24 s, a więc 20
rzędów wielkości mniej.
Dla nich era ta trwa bardzo długo.
Era leptonowa
10-4 s
Temperatura 1011 K (10 MeV)
Leptony (także neutrina) są w równowadze termodynamicznej
z promieniowaniem.
W epoce leptonowej, jedynymi relatywistycznymi
bozonami są fotony zaś relatywistycznymi fermionami
trzy generacje leptonów oraz ich antycząstki.
(e, e), (, ), (, )
Na początku ery leptonowej w
równowadze są procesy kreacji i
anihilacji par lepton – antylepton.
Liczba leptonów równa
liczbie fotonów
Era leptonowa
W miarę spadku temperatury (a więc i energii fotonów) następuje
najpierw nieodwracalna anihilacja taonów (jako najcięższych), a
następnie mionów.
Najdłużej utrzymuje się równowaga kreacji i anihilacji par
elektron – pozyton oraz ich oddziaływań z neutrinami.
e e
Temperatura progowa na produkcję
par elektron – pozyton T = 6109 K
Temperatura w środku Słońca
T = 15106 K
Era leptonowa
Pod koniec ery leptonowej, przy T < 1010 K (ok. 1 MeV), w
równowadze znajdują się następujące reakcje oddziaływań
słabych:
p e n e
n e p e
n
W równowadze, stosunek ilości neutronów i protonów
p
określony jest prawem Boltzmanna:
mn m p
n
kT
e
p
gdzie: (mn – mp) = 1,3 MeV
kT = 10 MeV dla T = 1011 K
Era leptonowa
n
W miarę ekspansji temperatura spada, a wraz z nią maleje p
(od ok. 0, 6 na początku ery leptonowej do ok. 0,2 pod jej
koniec).
Przy T 0,1 MeV równowaga słabych procesów stopniowo załamuje
się, a bardziej prawdopodobny staje się nieodwracalny rozpad beta:
n p e
Era leptonowa
Tuż po pierwszej sekundzie gęstość i temperatura zmalały tak, że
średni czas pomiędzy zderzeniami neutrin i antyneutrin przekroczył
czas życia Wszechświata, a ich średnia droga swobodna wzrosła na
tyle, iż stały się cząstkami swobodnymi.
Neutrina utraciły równowagę termodynamiczną z innymi cząstkami.
Powstało tło neutrinowe
Trudno je wykryć
doświadczalnie!
Era leptonowa
W 14 sekundzie temperatura spadła do 3109 K –
poniżej progu produkcji par elektron-pozyton
Elektrony i pozytony uległy
anihilacji, pozostawiając po sobie
olbrzymie ilości fotonów.
Zwiększenie
temperatury fotonów
Od tej chwili średnio na jeden nukleon przypadał
mniej więcej miliard fotonów.
Główne składniki Wszechświata to fotony i neutrina.
Nukleosynteza
Nukleosynteza – powstawanie jąder przez łączenie
się nukleonów lub lżejszych jąder - może zachodzić w
określonym przedziale temperatur:
•Temperatura zbyt niska – produkty reakcji mają za
małą energię, aby zbliżyć się dostatecznie.
• Temperatura za wysoka – powstałe w syntezie jądra
rozpadną się.
Nukleosynteza
1s
Temperatura 1010 K (0,1 MeV)
W okolicy tej temperatury mogą już utrzymać się produkty
pierwszej reakcji nukleosyntezy:
n p12D
Neutron ma w tych warunkach dwie możliwości:
1) reakcja z protonem i synteza deuteru,
2) spontaniczny rozpad beta.
Nukleosynteza
Przez pierwsze sekundy przybywa deuteru.
D
3
Gdy jego ilość względem wodoru osiągnie wartość 10
H
prawdopodobne stają się reakcje syntezy trytu i
izotopu 3He:
2
3
D
n
1
1T
2
1D
3
p2 He
Na skutek tych reakcji ubywa deuteru i jego obfitość stabilizuje się
stopniowo na poziomie około:
D
5
3
10
H
Nukleosynteza
23 He
5
3
10
Gdy względna koncentracja He osiągnie około
H
to zaczyna zachodzić kolejna reakcja:
3
2
He 23He 24He 2 p
Pewna niewielka część 4He zdąży jeszcze wejść w reakcje:
4
2
4
2
He T Li
3
1
7
3
He He Be
3
2
7
4
Nukleosynteza
Nukleosynteza kończy się po około 3 minutach.
Dla kolejnych reakcji, jak np. cykl 34He → 12C + γ jest już „za zimno”.
Wszechświat rozszerzając się ostygł do T 108 K
Po dalszych kilku tysiącach sekund radioaktywny tryt stopniowo
rozpada się na 3He, zaś 7Be przez wychwyt elektronu
przekształca się w 7Li.
Ustaliła się zasadnicza obfitość helu we Wszechświecie w ilości:
24 He
0,1
H
(22% - 24%) masy wodoru
stanowi masa 4He
Nukleosynteza
czas
Przebieg pierwotnej nukleosyntezy w czasie pierwszych
kilkunastu minut. Krzywe ukazują stopniowy wzrost (lub
spadek) obfitości poszczególnych nuklidów oraz
neutronów (n).
Nukleosynteza
Końcowa obfitość powstałych pierwiastków zależy
zasadniczo od dwóch czynników:
•tempa ekspansji — a więc i od tempa „stygnięcia”
Wszechświata,
•gęstości materii barionowej.
Porównując zmierzone obfitości różnych rodzajów jąder
z ilościami obliczonymi w modelach wczesnego
Wszechświata, można określić obecną gęstość materii
barionowej.
Względna zawartość: stosunek liczby
jąder do liczby jąder wodoru
Nukleosynteza
Najlepsze dopasowanie
4He
2H, 3He
7Li
Gęstość krytyczna
Nukleosynteza
Obserwowana obfitość 4He stała się też dodatkowo wskaźnikiem
testującym kwarkowo – leptonowy model budowy materii — a
konkretniej - wskaźnikiem ilości tzw. generacji kwarków i leptonów.
Znamy 3 rodziny leptonów:
(e, e), (, ), (, )
Tempo ekspansji i stygnięcia Wszechświata na etapie ery
leptonowej zależy od liczby rodzajów neutrin.
Tempo stygnięcia Wszechświata rzutuje z kolei na tempo reakcji
nukleosyntezy, a więc na końcową obfitość lekkich pierwiastków
np. 4He
Nukleosynteza
Teoretyczna obfitość
helu (jako procent masy) w
zależności od gęstości przy
różnych ilościach, N, typów
leptonów (i kwarków).
Era dominacji promieniowania
Po zakończeniu nukleosyntezy zawartość Wszechświata
jest następująca:
•Fotony
•Neutrina (tem. o 40% niższa od tem. fotonów)
•Elektrony (1 na miliard fotonów)
•Protony (1 na miliard fotonów)
•Jądra helu (23% masy protonów)
•Jądra 2H, 3He, 7Li (śladowe ilości)
Większość energii Wszechświata to energia fotonów
Era dominacji promieniowania
Przez ok. 300 tys. lat materia i promieniowanie są w równowadze
termodynamicznej (temperatura promieniowania równa jest
temperaturze materii).
Fotony w zderzeniach wymieniają enerię ze swobodnymi elektronami.
Na skutek zderzeń z elektronami
droga swobodna fotonów jest
bardzo mała.
Wszechświat jest
nieprzezroczysty dla
promieniowania
Ciało doskonale czarne
Era dominacji promieniowania
Gęstość energii promieniowania:
u a T 4
Obecna wartość (T = 2,73 K): u 10-34 g/cm3
Szacowana z obserwacji gęstość materii barionowej: ub 510-31 g/cm3
(prawie jeden atom na m3).
Obecnie materia dominuje nad promieniowaniem i
decyduje o geometrii i tempie ekspansji.
ub
u
104
t0
Era dominacji promieniowania
Gęstość promieniowania
u a T
4
1
R
4
Gęstość materii barionowej
ub
1
R3
Stosunek gęstości materii barionowej do gęstości promieniowania
zmienia się wraz z rozmiarem Wszechświata:
ub
R(t )
u
Obecnie wynosi 104, kiedy Wszechświat był 104 razy
mniejszy ub i u były równe.
Do tej chwili trwała era dominacji promieniowania
Era dominacji promieniowania
Era dominacji promieniowania – gęstość energii
promieniowania jest większa niż gęstość materii
barionowej (uγ > ub)
•Rozpoczyna się, gdy wiek Wszechświata wynosi kilkanaście
minut (od Wielkiego Wybuchu) przy temperaturze T ≈ 109 K
•Trwa kilka tysięcy lat, gdy w trakcie ekspansji temperatura
spadnie do około 3104 K.
Rozseparowanie materii i promieniowania
380 000 lat
Temperatura 3000 K
Protony i jądra przyłączają elektrony (rekombinacja) – tworzą się atomy.
Promieniowanie nie jest w stanie istotnie oddziaływać z
materią — nie jest w stanie w efektywny sposób jonizować
i wzbudzać atomów.
Materia nie ma wpływu na promieniowanie promieniowanie reliktowe
Od tej chwili temperatura
promieniowania maleje
wraz z ekspansją
Wszechświata:
1
T
R
Obecna wartość T = 2,73 K
Promieniowanie reliktowe
Energia fotonu:
E
hc
Średnia energia fotonu
zależy od temperatury:
E cons T
Średnia energia fotonu
maleje wraz z temperaturą
3000 K
Długość fali fotonu rośnie
2,73 K
temperatura
Promieniowanie reliktowe
W 1964 r. Arno Penzias i Robert Wilson odkryli promieniowanie tła.
1992 r. sonda kosmiczna COBE
Widmo promieniowania
tła zgadza się z widmem
promieniowania ciała
doskonale czarnego.
Wyniki COBE
T = (2,7250,002) K
2001 r. sonda kosmiczna WMAP (Wilkinson Microwave
Anizotropy Probe)
Promieniowanie reliktowe
Eksperyment WMAP
Sonda kosmiczna wystrzelona 30.06.2001 roku
Pomiar promieniowania mikrofalowego w 5
przedziałach częstości: od 23 GHz (13 mm)
do 94 GHz (3,2 mm).
Porównanie pomiarów w różnych zakresach częstości
umożliwia odjęcie tła pochodzącego od Galaktyki.
Aby zminimalizować tło pochodzące od Ziemi i Słońca sondę
umieszczono na orbicie wokół tzw. punktu Lagrange’a
Quasi-stabilna konfiguracja WMAP – Ziemia -Słońce
Eksperyment WMAP
1. Trzy pętle wokół Ziemi
2. Wykorzystanie
grawitacji Księżyca
WMAP na orbicie –
„tyłem” do Ziemi i Słońca
Eksperyment WMAP
Różne kolory oznaczają
różne temperatury.
Fluktuacje temperatury
promieniowania tła –
fotografia rozkładu materii
we Wszechświecie w wieku
380 000 lat .
Mapa temperatur Ziemi.
Bez fluktuacji gęstości nie
powstałyby galaktyki.
Eksperyment WMAP
W pierwszym przybliżeniu
promieniowanie jest
izotropowe (T 1 K)
Wpływ ruchu Ziemi względem
„globalnego” układu z prędkością
337 km/s (T 1 mK)
Po odjęciu efektu Dopplera
widzimy promieniowanie naszej
Galaktyki (T 200 K)
Po odjęciu promieniowania
Galaktyki i innych znanych źródeł
(T 100 K)
Eksperyment WMAP
Eksperyment WMAP
Przed fazą rekombinacji istniały w ośrodku fluktuacje gęstości
energii (i temperatur).
Obszary o gęstości większej niż
średnia, kurczyły się pod wpływem
grawitacji i nagrzewały.
Jednocześnie wzrastające z
temperaturą ciśnienie
promieniowania prowadziło do
zahamowania kolapsu i do
rozszerzania.
Obszar taki oscylował z amplitudą i częstością, które związane były
z warunkami fizycznymi ośrodka.
Eksperyment WMAP
W chwili przed rozpoczęciem
inflacji:
t = 10-34 s, kT 1014 GeV
Maksymalna odległość
między punktami
połączonymi przyczynowo:
ct 10-26 m
Zasada nieoznaczoności
spowoduje wystąpienie
różnic temperatury rzędu:
c
kT
1010 GeV
ct
Fluktuacje temperatury i gęstości:
kT
10 4
kT
Świat Nauki 04-2004
Eksperyment WMAP
Typowa amplituda fluktuacji
Dwie krzywe teoretyczne
obliczone dla różnych gęstości
materii Wszechświata.
Kątowe rozmiary fluktuacji
Eksperyment WMAP
Typowe rozmiary fluktuacji odpowiadają „horyzontowi akustycznemu” —
czyli rozmiarowi, jaki może przebiec dźwięk w ciągu ok. 300 000 lat.
Rozmiar takiego „horyzontu” można teoretycznie oszacować i
policzyć, jakie powinny być rozmiary kątowe takiego horyzontu,
rzutowane dzisiaj na sferę niebieską.
Rozmiary te zależą od geometrii Wszechświata.
płaski
zamknięty
otwarty
Eksperyment WMAP
Precyzyjny pomiar korelacji kątowych w promieniowaniu tła
umożliwił jednoczesne dopasowanie wielu parametrów.
Dominują fluktuacje o
rozmiarach kątowych
rzędu 0,80.
tot 1,02 0,02
k
Wszechświat jest płaski!
Porównanie amplitud maksimów pozwala oszacować ilość
ciemnej materii we Wszechświecie.
Eksperyment WMAP
Pierwsze maksimum:
Ciemna materia moduluje sygnały
akustyczne w promieniowaniu tła.
Po inflacji gęstsze obszary ciemnej
materii wciągają siłami grawitacji
bariony i fotony.
W epoce rekombinacji efekty
grawitacji i fali akustycznej sumują
się.
Drugie maksimum:
Skupiska ciemnej materii
odpowiadające fali drugiego
maksimum na długo przed
rekombinacją maksymalizują
temp. promieniowania w
dolinach. Jest to punkt zwrotny –
ciśnienie gazu zaczyna wypychać
bariony i fotony z dolin. Efekt –
drugie maksimum jest niższe.
Świat Nauki 04-2004
Eksperyment WMAP
Stwierdzono polaryzację
promieniowania mikrofalowego
w dużych skalach kątowych na
niebie.
Polaryzacja spowodowana
rozpraszaniem na cząstkach
naładowanych.
Kilkaset milionów lat po Wielkim Wybuchu około 17% fotonów
promieniowania reliktowego było rozpraszanych przez zjonizowany gaz.
Powstał on w wyniku powtórnej jonizacji kosmicznego wodoru i helu
przez promieniowanie pochodzące z pierwszego pokolenia bardzo
masywnych i gorących gwiazd.
Wniosek:
Pierwsze gwiazdy w epoce 200 - 300 mln lat po Wielkim Wybuchu.
Eksperyment WMAP
Wyniki:
Atomy (bariony) wypełniają tylko 4%
Wszechświata.
23% stanowi ciemna materia
73% to „ciemna energia”, którą
opisujemy przez stałą kosmologiczną.
„Ciemna energia” powoduje
przyspieszenie ekspansji Wszechświata!
Wiek Wszechświata –13,7 mld lat (z dokł. 1%)
Promieniowanie reliktowe pochodzi z okresu 379 000 lat po Big Bang
Pierwsze gwiazdy powstawały 200 mln lat po Big Bang
Polaryzacja promieniowania – dodatkowy dowód teorii inflacji.
Eksperyment Planck
Planowany na rok 2007 dostarczy
jeszcze dokładniejszych danych o
promieniowaniu reliktowym:
•Mapa promieniowania z rozdzielczością 5 - 10 minut
kątowych z dokładnością do 10-6 K
•Polaryzacja promieniowania – test teorii inflacji.
Powstawanie gwiazd
Tempo pojawiania
się formacji
gwiazd począwszy
od Wielkiego
Wybuchu.
A. Feild (STScI).
1028
grawitacja
Temperatura (K)
1015
Promieniowanie
reliktowe
1013
Nukleosynteza
102
Gęstość jądrowa
10-6
Unifikacja oddz.
elektrosłabych
10-11
Plazma
kwarkowogluonowa
Czas (s)
oddz. silne
1013
elektromagnetyzm
109
oddz. słabe
103
10-35
Inflacja
Wielka unifikacja
10-43
1038
Kwantowa grawitacja?