Skala decybelowa

1
Skala decybelowa
Często odnosimy wartość jakieś wielkości do wartości odniesienia tej samej wielkości. Mówimy
wówczas, że dana wartość jest x –razy większa (lub mniejsza) od znanej wartości odniesienia.
Wprowadźmy oznaczenia:
W – dowolna wartość jakieś wielkości, posiada jednostkę
Wo – znana wartość odniesienia tej samej wielkości, wyrażona w tych samych jednostkach co wartość
W
Stosunek tych dwóch wartości nazywamy wartością względną danej wielkości. Wartość względna nie
posiada jednostki. Wartość względną oznaczmy jako k. Zatem
=
(1)
Czasem stosunek k, czyli wartość względna, jest bardzo duża liczbą, rzędu bilionów lub bardzo małą,
kilkadziesiąt zer po przecinku. Jest to niewygodne dla zapisu i odczytania i może powodować pomyłki.
Dlatego wygodnie jest wygodnie wyrażać wartość bezwzględną jako logarytm dziesiętny z wartości
bezwzględnej. Jednostką wartości logarytmu z wartości bezwzględnej jest bel [B], ale częściej
stosujemy podwielokrotność tej jednostki, decy- (skrót d) czyli używamy decybela. Wartość
bezwzględna w belach obliczamy:
=
[B]
(2)
w decybelach ta sama wartość względna ma postać
= 10 ∙
[dB]
(3)
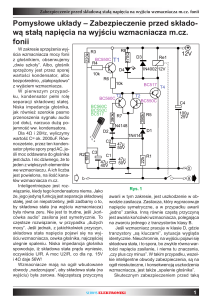
W elektrotechnice i elektronice często chcemy badać zależność niektórych wielkości od częstotliwości
np. wzmocnienie, moc wyjściową czy napięcie wyjściowe wzmacniacza. Jeśli na wejście wzmacniacza
podajemy napięcie sinusoidalne o nastawialnej częstotliwości, a do wyjścia wzmacniacza przyłączymy
rezystor, to mierząc napięcie na tym rezystorze, zauważymy, że napięcie zmienia się wraz z
częstotliwością. Jeśli będziemy mierzyć moc pobraną przez ten rezystor, to również zauważymy, że
moc wyjściowa zależy od częstotliwości napięcia sinusoidalnego na wejściu wzmacniacza. Uwaga: Do
pomiaru mocy wyjściowej wzmacniacza nie używamy watomierza, lecz miernika mocy wyjściowej.
Dla częstotliwości dużo większych niż 50 Hz, watomierz wskazywałby wartości znacznie odbiegające
od rzeczywistych.
Dla pewnej częstotliwości, napięcie wyjściowe ma największą wartość, którą określimy jako Umax, a
przy tym napięciu wydziela się na rezystorze największa moc, którą określimy jako Pmax. Niech P
oznacza dowolną wartość mocy wyjściowej, oczywiście mniejsza niż Pmax.
Moc względną możemy wyrazić jako stosunek
=
(4)
Wyrażenie to jest liczbą niemianowaną, czyli nie posiada jednostki. Możemy również ten stosunek
wyrazić w procentach, ale wówczas należy pomnożyć to wyrażenie przez 100%.
2
Możemy również moc względną wyrazić w decybelach i wówczas zapis będzie następujący:
= 10 ∙
[
]
(5)
W praktyce, wygodniej jest mierzyć napięcie niż moc. Można wówczas wyznaczyć napięcie wyjściowe
względne jako stosunek dowolnej wartości napięcia wyjściowego U do wartości maksymalnej Umax.
=
(6)
Pamiętamy z elektrotechniki matematyczną zależność mocy od napięcia.
P=
(7)
wzórtendotyczydowolnejwartościmocyPinapięciaU.Dlawartości
maksymalnejmocybędziewzórmiałpostać:
Pmax=
9:;
(8)
Obliczmy moc względną i wstawmy za P i Pmax wyrażenia (7) i (8).
=
=
?
?
@
@
=
9:;
=(
)2 (9)
Stwierdzamy,żemocjestproporcjonalnadokwadratunapięcia.
Powstawieniuwyrażenia(9)dowzoru(5),możemyobliczyćnapięciewzględnewyrażonew
decybelach.Otrzymamywówczas:
= 20 ∙
[
](11)
Wzory (5) i (11) będą nam bardzo pomocne do wyznaczenia spadków mocy i napięć na wyjściu
wzmacniacza.
Rozpatrzmy stan pracy wzmacniacza, gdy moc na wyjściu wzmacniacza jest o połowę mniejsza niż
moc maksymalna, czyli
=
= 0,5
(12)
Chcemy wyrazić moc względną w decybelach, więc obliczmy logarytm dziesiętny z liczby 0,5. Można
skorzystać z kalkulatora z funkcją obliczania wartości logarytmów lub z tablic logarytmicznych.
log0,5=-0,3010[B]
(13)
Jeśliwyrazimytęwartośćwdecybelach,tobędziemiałaonapostać:
log0,5=-3,01[dB] (14)
3
Ponieważ moc jest zawsze proporcjonalna do kwadratu napięcia, zgodnie ze wzorem (9), obliczmy
jaka będzie zależność matematyczna pomiędzy danym napięciem U, a napięciem maksymalnym
Umax przy spadku mocy -3 dB.
Wyznaczmy wartość stosunku danego napięcia do napięcia maksymalnego.
O
=
=P
→
Sprawdzamy: 20 ∙
Q
= PO =
Q
= 20 ∙
√O
Q
√O
≅ 0,707 (15)
≅ 20 ∙ log(0,707) ≅ −3,01
(16)
Zmianie mocy wydzielonej w odbiorniku o -3 dB odpowiada zmiana napięcia na tym
Q
odbiorniku ≅ 0,707 razy.
√O
Możemy napisać wzór:
Uwy(-3dB) = 0,707 Uwymax
(17)
Konsekwentnie wzmocnienie napięciowe wynosi
Ku (-3dB) = 0,707 Kumax
(18)
Mówimy, że na wyjściu rezystora nastąpił spadek mocy –3 dB, jeśli dana moc wyjściowa P jest
dwukrotnie mniejsza od mocy maksymalnej Pmax. Częstotliwość, przy której moc na rezystorze na
wyjściu wzmacniacza jest dwukrotnie mniejsza nazywamy częstotliwością graniczną, czyli przy spadku
mocy -3 dB. Przy takim spadku mocy, np. filtru aktywnego środkowoprzepustowego, definiujemy
częstotliwości graniczne, górną i dolną fd i fg. Są to częstotliwości przy których wzmocnienie
napięciowe zmienia się o -3 dB, czyli zachowana jest zależność (18).
Przeanalizujmy stosunek mocy P do Pmax równy 100 i obliczmy moc względną
kP=
=0,01
(19)
Teraz obliczmy moc względną kP w belach,
=
[ ]
i w decybelach
= 10 ∙
[
(20)
]
(21)
Jeśli w naszym przypadku ten stosunek wynosi 0,01, to obliczmy logarytm dziesiętny z tej liczby.
kB = log 0,01 = -2 [B]. Jeśli chcemy to wyrazić w decybelach, to kdB = 10 · (-2) = -20 dB
Jeśli moc wyjściowa jest 100 razy mniejsza od mocy maksymalnej, to mówimy, że nastąpił spadek
mocy o 20 decybeli.
Pamiętamy, że moc jest wprost proporcjonalna do kwadratu napięcia, więc obliczmy jaki jest
stosunek danego napięcia do napięcia maksymalnego. Przypomnijmy sobie wzór
=
=
O
O
(9), więc
→
=P
Q
Q
= PQWW = QW = 0,1
(22)
4
Sprawdzamy: 20 ⋅ log
Y
YZ[\
= 20 ⋅ log
Q
QW
= 20 ⋅ log(10]Q ) = −20dB
(23)
Jeżeli więc stosunek mocy P do mocy odniesienia Pmax wynosi 1/100, to wartość stosunku napięcia U
do wartości odniesienia Umax jest 1/10. Mówimy, że nastąpił spadek mocy -20dB. Zapiszmy to w
postaci wzorów matematycznych:
Uwy(-20dB) = 0,1 Uwymax
(24)
Konsekwentnie wzmocnienie napięciowe wynosi
Ku (-20dB) = 0,1 Kumax
(25)
Dla spadku mocy -20 dB możemy również wyznaczyć częstotliwości graniczne, górną i dolną fd
i fg. Są to częstotliwości przy których wzmocnienie napięciowe zmienia się o -20 dB, czyli zachowana
jest zależność (25).
Znajomość powyższych określeń jest bardzo przydatna przy opracowywaniu projektów
egzaminacyjnych w zawodzie technik elektronik. W minionych latach na egzaminie, zdający abiturient
miał za zadanie wyznaczyć pasmo przenoszenia wzmacniacza lub filtru aktywnego. Zatem warto
poznać te określenia i zależności, aby nie mieć trudności przy opracowywaniu projektu
egzaminacyjnego.
Opracowała:
Jadwiga Balicka