Slide 1

Badanie strutury powierzchni z atomową
zdolnością rozdzielczą
Powierzchnia – jak ją zdefiniować ?
Obszar kryształu, dla którego nie da się zastosowa
Definicja robocza
2-3 ostatnie warstwy atomowe
mikroelektronika
kserograf
tarcie
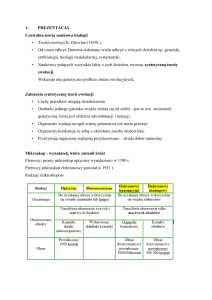
Technologie wykorzystujące zjawiska zachodzące na powierzchniach – drobne przykłady
adhezja
zwilżanie
utwardzanie
nośniki
pamięci
kataliza
10 -1
10 0
10 1
10 2
Skala długości, nm
10 3
generacja
drugiej
harmonicznej
korozja
nowe
materiały
światłowody
zabarwienia
materiałów
filtry
Badanie strutury powierzchni z atomową
zdolnością rozdzielczą
Informacja o symetrii powierzchni
dyfrakcja niskoenergetycznych elektronów (Low
Energy Electron Diffraction) – LEED

dyfrakcja odbiciowa wysokoenergetycznych
elektronów (Reflection High Energy Electron
Diffraction) – RHEED

holografia elektronowa

rozpraszanie jonów (Ion scattering spectroscopy
- ISS



kanałowanie jonów - channeling
Badanie strutury powierzchni z atomową
zdolnością rozdzielczą
Informacja o lokalnym otoczeniu –
atomowa zdolność rozdzielcza

mikroskop polowy – (Field Ion
Microscope) - FIM

skaningowy mikroskop tunelowy
(Scanning Tunneling Microscope)
– STM

mikroskop sił atomowych (Atomic
Force Microscope) – AFM
Czy elektrony mogą wydostać się ponad
powierzchnię ?
Uproszczony model pasmowy metalu (bariera o wysokości j)
Próżnia
Metal
j – praca wyjścia z metalu
EF – poziom Fermiego
Wnikanie do bariery
Obszar A)
Na zewnątrz x < 0
H= -(2/2m) (d2/dx2)
Wewnątrz x  0 H= -(2/2m) (d2/dx2)+V
Obszar B)
Szukamy rozwiązań w postaci:
dla x < 0
dla x  0
A) (x)  A eikx  B e ikx
k  (2mE /  2 )
B) (x)  C eik x  D eik x
k '  2m ( E  V ) /  2
'
'
Wewnątrz bariery k’ jest urojone k’=i
( x )  C e   x  D e  x
 więc D=0
Prawdopodobieństwo znalezienia elektronu wewnątrz bariery (obszar B)
P | ( x) |2 | C |2 e 2 x
  (2m(V  E) /  2 )1/ 2  (2mj /  2 )1/ 2
j - praca wyjścia z metalu
Funkcja falowa elektronu nie kończy się na powierzchni metalu, lecz wnika do
próżni. Prawdopodobieństwo znalezienia elektronu w próżni ~ exp(-2 x)
Metal w zewnętrznym polu elektrycznym
W miarę oddalania się od powierzchni
metalu elektron będzie „odczuwał”
następujący potencjał V(z)
V(z)=Vmetal+ Vobraz + Vpole
Vpole= - E ·z
Vobraz = -1/(4o) e/(2z)
j0 – efektywna wysokość bariery
(można ją znaleźć z warunku V(z0))
EF – położenie poziomu Fermiego
Prawdopodobieństwo przejścia przez barierę liczone w metodzie WKB

P ~ exp  23 / 2 m1/ 2 / 
 V(z)  E
zc
1/ 2
0
dz
E – energia kinetyczna cząstki o masie m
V(z) – energia potencjalna elektronu
zc – szerokość bariery
Przejście przez barierę – inne podejście
H  ( 2 / 2m)(d 2 / dx 2 )
H  ( 2 / 2m)(d 2 / dx 2 )  V
na zewnątrz barier
wewnątrz barier
V = (j1 + j2)/2
D=0 bo brak ruchu w kierunku –x o obszarze C
C
A
B
Dla x  0
(x)  A eikx  B e ikx
Dla x  a
 ( x)  C eikx  De ikx
ik ' x
 ik x
Dla 0  x  a  ( x )  E e  Fe
, gdzie k '  2m(E  V) /  2
Warunki brzegowe:
F=0 by   
k '  i   2m(V  E) /  2
 (x) i d/dx muszą być ciągłe w x=0 i w x=a
2
Ostatecznie otrzymujemy, że współczynnik przejścia
C
1

A
 V sinh 2  a  
1  4E (V  E ) 


Prawdopodobieństwo tunelowania
2
C
1
P

A
 V sinh 2  a 
1  4E (V  E) 


Prawdopodobieństwo tunelowania P dla || a >> 1
Pe
2  a
  2m j /  2
Równanie Nordheima
Dokładną gęstość prądu tunelowania j można wyliczyć z zależności
j=1.54x10-6 E 2/j t2(y) exp[-6.83x107 j3/2 f(y)/ E]
,
gdzie f(y) jest stabelaryzowaną funkcją bezwymiarowego
parametru y
y= e3/2 E 1/2 / j
Powyższe równanie można zapisać w postaci
I = a U2 exp(-b j3/2/cU)
Gdzie a,b,c są stałymi, I prądem emisji, a U przyłożonym napięciem.
Jak uzyskać duże E ?
E ~ q/r2
R0 i r  0
dla r  R0
E
Szukamy elektrod o ostrych końcach
Mikroskop polowy
Elektrony będą emitowane z miejsc, w których potencjał szybko się
zmienia, czyli np. z okolic, gdzie występują defekty, czy też gdzie
ulokowane są atomy.
Powiększenie M =D/d
M =L/R0 = 15 cm/10nm  105  107
Co się stanie, gdy w pobliżu powierzchni
próbki umieścimy sondę ?
Próbka
Sonda
Prawdopodobieństwo tunelowania P dla ||a >> 1
16 E (j  E) 2  a
P
e
2
j
, gdzie
  2 m( j  E ) /  2
j1  j 2
j
2
Prąd tunelowy – przypadek ogólny
Model ostrza z falą typu s
I  323h 1e2 V02sa (EF )R2t 4e2  R t   (r0 ) 2(E  EF )
I(d)  V sa (E F )e 1.025
jd
,
gdzie odległość [d] w Å, a średnia
praca wyjścia [j] w eV
Prąd tunelowy ( jednostki umowne)
Cała informacja o strukturze elektronowej „siedzi” w
gęstości stanów elektronowych próbki sa
Odległość ostrze-próbka ( Å )
Spektroskopia STM
Korzystając z mikroskopu STM można określić gęstość stanów 
badanej powierzchni.
Jeżeli element macierzowy przejścia jest stały, prąd tunelowania I można
przybliżyć wyrażeniem:
eU
I   SA (E F  eU  )d
EF – energia Fermiego,
U – napięcie na próbce.
0
Pochodna dI/dU pozwala wyznaczyć gęstość stanów na poziomie
EF-eU
dI
 SA (E F  eU)
dU
Zmieniając U badamy kształt pasm
Przepływ elektronów
Kierunek przepływu elektronów zależy od polaryzacji próbki
Próbka spolaryzowana
ujemnie
Próbka spolaryzowana
dodatnio
Jak zbudować mikroskop ?
Mikroskop skaningowy musi posiadać:
Ostrze
 Układ umożliwiający precyzyjne przesuwanie ostrza
 Układ umożliwiający tłumienie drgań.

Ostrze
Przypadek idealny
Przypadek rzeczywisty
Ostrze
jp 

U
exp  A j d
d

jp - prąd tunelowy (0.1-10 nA);
j  uśredniona praca wyjścia elektrody i ostrza ( kilka eV ).
A ~ 1.025 eV-1/2 Å-1
U - napięcie pomiędzy podłożem i ostrzem ( kilka V )
d - odległość ostrza od podłoża ( ~ Å )
Za względu na silną zależność prądu tunelowania od odległości, jedynie atom
znajdujący się najbliżej powierzchni jest aktywny.
Jak przesuwać ostrze ?
Zjawisko piezoelektryczne
Odkrywcy: 1880 Piotr i Paweł Curie
Przy ściskaniu lub rozciąganiu niektórych kryształów na ich
krawędziach pojawiają ładunki elektryczne.
Materiały piezoelektryczne: kwarc, turmalin, sól Saignette’a, tytanian baru,
piezoceramiki Pb(Ti,Zr)O3 (PZT) i inne.
Komórka elementarna kwarcu SiO2
(wiązanie jonowe)
Si
O
Kwarc
Przesunięcie jonów spowodowało, że na ściankach kryształu
prostopadłych do osi X1 wydzielił się ładunek
Podobne efekt pojawi się, gdy kryształ ściśniemy wzdłuż osi X2 i X3.
Przyłożenie zewnętrznego pola elektrycznego wymusi ruch jonów krzemu i tlenu,
a tym samym zdeformuje kryształ
Przyłożenie napięcia elektrycznego U powoduje odkształcenia
kryształu Dxi
Dxi = a U
Skaner
Odkształcenia Dxi są w pewnym zakresie
proporcjonalne do przyłożonego napięcia U
Dxi = ai U
|ai| = 1 - 6 Å / V
Skaner może być walcem wykonanym z piezoelektryka, podzielonym na 4
sektory. Do przeciwległych sektorów przykładamy napięcia o takich samych
wartościach, lecz przeciwnych znakach. Po przyłożeniu napięcia odpowiedni
sektor wydłuża się lub skraca, przechylając igłę zamocowaną na końcu
skanera.
Tłumienie drgań
Aby uzyskać atomową zdolność rozdzielczą odległość pomiędzy ostrzem a
próbką musi być utrzymywana z dokładnością 0.01 Å.
Należy wyeliminować drgania !!!!
Drgania mogą być powodowane przez:
wibracje budynku 15-20 Hz
 biegnących ludzi 2-4 Hz
 pompy próżniowe
 dźwięk.

Drgania można eliminować poprzez:



zawieszenie mikroskopu na sprężynach ( z dodatkowym tłumieniem przy
pomocy prądów wirowych)
pneumatyczne podpórki izolujące
zwiększenie masy własnej podstawy.
Skaningowy Mikroskop Tunelowy
Stacjonarny uchwyt na próbki
10 mm skaner
piezoelektryczny
Izolacja
drgań
Inercyjny układ
transportu
Uchwyt ma próbkę
8 calowa flansza UHV
Pracownia układów mezoskopowych
Zakładu Fizyki Doświadczalnej UJ
Skaningowy mikroskop elektronowy (SEM)
STM
STM mechanika
Transmisyjny mikroskop elektronowy (TEM)
Transmisyjny mikroskop elektronowy (TEM)
Mody pracy
Mod stałoprądowy
Skaner zmienia odległość pomiędzy
ostrzem a próbką w taki sposób, aby
prąd tunelowania był stały. Mierzone jest
napięcie przyłożone do elementów
piezoelektrycznych. To napięcie jest
następnie przeliczane na zmianę
długości tych elementów.
Ten sposób pracy jest zalecany, gdy nie znamy morfologii próbki
lub, gdy powierzchnia jest silnie pofałdowana
Mody pracy
Mod stałonapięciowy
Odległość pomiędzy ostrzem a próbką jest
stała. Mierzone są zmiany prądu
tunelowego.
Ten sposób pracy jest zalecany, gdy badamy gładkie powierzchnie.
Ze względu na silną zależność pomiędzy prądem tunelowania a
odległością igła-próbka, przy tym sposobie pracy osiąga się dużą
rozdzielczość.
Uwaga: Łatwo uszkodzić igłę.