laboratoria elektryczne - IMiUE

POLITECHNIKA ŚLĄSKA
WYDZIAŁ INŻYNIERII ŚRODOWISKA I ENERGETYKI
INSTYTUT MASZYN I URZĄDZEŃ ENERGETYCZNYCH
BADANIE TRANSFORMATORA
TRÓJFAZOWEGO
(E-13)
Opracował: mgr inż. Janusz Mędrych
Sprawdził:
Zatwierdził:
www.imiue.polsl.pl/~wwwzmiape
3
BADANIE TRANSFORMATORA TRÓJFAZOWEGO
1. Cel ćwiczenia
Celem ćwiczenia jest wyznaczenie charakterystyk stanu jałowego i stanu zwarcia
transformatora trójfazowego oraz dokonanie analizy własności transformatora jako
maszyny elektrycznej. Wykonane pomiary umożliwią wyznaczenie wartości
parametrów elementów schematu zastępczego transformatora.
2. Wprowadzenie
Transformator jest statyczną maszyną elektryczną, służącą do przetwarzania
(transformacji) energii elektrycznej. Celem transformacji jest podwyższanie lub
obniżanie napięcia, co powoduje zmniejszanie lub zwiększanie wartości natężenia
prądu. Przetwarzanie energii odbywa się za pośrednictwem pola magnetycznego.
Uproszczoną budowę transformatora trójfazowego przedstawia rysunek 1.1.
Rys. 1.1. Budowa transformatora trójfazowego
Na ferromagnetycznym rdzeniu nawinięte są odizolowane od rdzenia uzwojenia
Rdzeń transformatora, stanowiący jego obwód magnetyczny, jest przeważnie
4
wykonany z cienkich, wzajemnie od siebie odizolowanych blach stalowych.
Uzwojenia
wykonuje
się
z
izolowanego
drutu
miedzianego.
Właściwości
transformatora, jak każdej maszyny elektrycznej, opisywane są dla trzech
charakterystycznych stanów pracy: jałowego, obciążenia i zwarcia.
Straty mocy czynnej podczas pracy transformatora występują w rdzeniu ze
względu na prądy wirowe i histerezę magnetyczną, a także w uzwojeniach z powodu
mocy wydzielanej na ich rezystancjach.
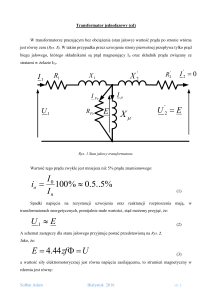
2.1. Stan jałowy transformatora
Transformator znajduje się w stanie jałowym, jeżeli uzwojenie pierwotne jest
zasilane napięciem U1 ze źródła, a obwód wtórny jest rozwarty (prąd I2 = 0). Prąd
stanu jałowego I0 wynosi od kilku do kilkunastu procent wartości prądu
znamionowego strony pierwotnej. Prąd I0 płynąc przez uzwojenie pierwotne wytwarza
w rdzeniu transformatora strumień magnetyczny główny Φ i strumień rozproszenia
Φ1R zamykający się w powietrzu (w uzwojeniu wtórnym prąd nie płynie, w związku
z tym nie jest wytwarzany strumień rozproszenia Φ2R). Strumień główny indukuje
w uzwojeniach siły elektromotoryczne odpowiednio E1 i E2 = U2. Strumień
rozproszenia Φ1R indukuje siłę elektromotoryczną E1R = UX1. Schematycznie
powstające strumienie magnetyczne przedstawiono na rysunku 1.2.
I0
Φ
U1
Φ1R
U2
Rys. 1.2. Strumienie magnetyczne w rdzeniu transformatora w stanie jałowym
Analizę pracy transformatora (i innych maszyn elektrycznych) wygodnie jest
przeprowadzać opierając się na schemacie zastępczym i wykresie wektorowym napięć
i prądów. Schemat zastępczy jest ścisły, gdy uwzględnia wszystkie istotne zjawiska,
występujące przy pracy danej maszyny. Sporządzając schemat zastępczy
transformatora w stanie jałowym, uwzględniamy w nim następujące elementy:
 Xμ
– reaktancję indukcyjną związaną ze strumieniem głównym Φ,
 X1R – reaktancję indukcyjną związaną ze strumieniem rozproszenia Φ1R,
5
 R1
– rezystancję uzwojenia strony pierwotnej transformatora,
 RFe – rezystancję obrazującą wspólne (z histerezy i z prądów wirowych)
straty mocy w rdzeniu.
Przy sporządzaniu schematu zastępczego przeważnie pomija się straty mocy
w materiałach izolacyjnych, prądy pojemnościowe i prądy upływu. Przy rysowaniu
schematu nie uwidacznia się też strony wtórnej transformatora (prąd I2 = 0).
Transformator w stanie jałowym zachowuje się jak odbiornik z rdzeniem stalowym
(dławik). Schemat zastępczy i wykres wektorowy transformatora w stanie jałowym
przedstawiono na rysunku 1.3.
Rys. 1.3. Schemat zastępczy i wykres wektorowy (1 faz.) transformatora w stanie jałowym
Dla przedstawionego na rys. 1.3. schematu można napisać równanie Kirchhoffa:
U

U

U

E

R

I

jX

I

jX

I
1
0
0
μ
1
R1
X1
1
1
R

(1)
Moc czynna pobierana przez transformator w stanie jałowym zamienia się
w całości na ciepło [4] i prawie w całości są to straty w rdzeniu. Znając rezystancję
uzwojenia pierwotnego R1 i moc pobieraną w stanie jałowym P0 (w jednej fazie),
możemy zapisać:


2
3
P

I

R

ΔP

ΔP

ΔP
0
0
1
Fe
H
W
gdzie:
ΔP

ΔP

ΔP
Fe
H
W – straty w rdzeniu,
ΔPH
– straty na histerezę (przemagnesowywanie),
ΔPW
– straty na prądy wirowe.
(2)
6
Znając wartość strat całkowitych ΔPFe w funkcji częstotliwości f, można
wyznaczyć udział strat na histerezę i na prądy wirowe z zależności:
2
ΔP
k
B
f
H
H m
(3)
2 2
ΔP

k B
f
W W m
(4)
gdzie:
Bm
– amplituda indukcji magnetycznej,
f
– częstotliwość napięcia zasilania (zmienna niezależna),
kH, kW – współczynniki stałe możliwe do wyznaczenia z prostej regresji (5),

P
Fe

k

k
f.
H
W
2
fB
m
(5)

P
0

współczynnik mocy stanu jałowego – cos
,
0
U

1I
0

przekładnię transformatora
U1
–  U ,
2

składową czynną prądu jałowego
2
2
P

I

R

I

R
0
0
1 P
0
0
1


– I
,
(8)
Fe
E
U
1
1

składową bierną prądu jałowego
2
2
– Iμ  I0IFe,
(6)
(7)
(9)
oraz przybliżone parametry schematu zastępczego RFe i X  :
E UU
X
 1 1 1,
μ
I
I
I0
μ
μ
2
2
2
3E
U
U
1
1
1
R



Fe
.
2
ΔP
P

I

R
Fe(1f)
0
0
1 P
0
(10)
(11)
2.2. Stan obciążenia transformatora
Transformator znajduje się w stanie obciążenia, jeżeli uzwojenie pierwotne jest
zasilane napięciem U1 ze źródła, a do obwodu wtórnego przyłączony jest odbiornik
o impedancji Z. Prądy I1 i I2 płynące przez uzwojenia pierwotne i wtórne wytwarzają
w rdzeniu transformatora strumień główny Φ i strumienie rozproszenia Φ1R
(uzwojenia pierwotnego) oraz Φ2R (uzwojenia wtórnego), zamykające się przez
powietrze (strumień Φ2R indukuje SEM E2R = UX2). Schematycznie powstające
strumienie magnetyczne przedstawiono na rysunku 1.4.
7
I1
I2
Φ
Φ1R
U1
Φ2R
U2
Z
Rys. 1.4. Strumienie magnetyczne w rdzeniu transformatora w stanie obciążenia
Prąd strony wtórnej I2 zależy od napięcia na zaciskach uzwojenia wtórnego U2
oraz od parametrów odbiornika Z. Prąd strony pierwotnej I1 dopasowuje się do prądu
obciążenia I2 oraz do prądu I0. Prąd I0 ma dwie składowe: składową bierną Iμ
niezbędną do magnesowania obwodu rdzenia i składową czynną IFe reprezentującą
globalne straty w rdzeniu. Sporządzając schemat zastępczy transformatora w stanie
obciążenia, należy uwzględnić (poza wymienionymi w p. 2.1.) następujące elementy:
 X2R – reaktancję indukcyjną związaną ze strumieniem rozproszenia Φ2R,
 R2 – rezystancję uzwojenia strony wtórnej transformatora.
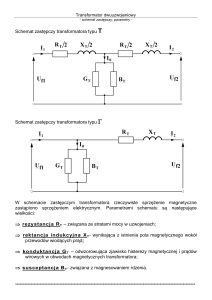
Schemat zastępczy transformatora w stanie obciążenia przedstawiono na rysunku 1.5.
I1
R1
X1R
Transformator I2
UX1
E1
RFe
UX2
UR2
I
IFe
U1
R2
idealny
I0
UR1
X2R
E1
X
E2
U2
Z

Rys. 1.5. Schemat zastępczy (1 faz.) transformatora w stanie obciążenia (postać I)
Dla przedstawionego na rys. 1.5. schematu można napisać równania Kirchhoffa
zarówno dla strony pierwotnej, gdzie przyjmuje ono postać równania (1):
U
U

U

E
1
,
1
R1
X1
(12)
jak i dla strony wtórnej w postaci:
E
U

U

U
2
.
X2
R2
2
(13)
Bardzo często schemat zastępczy transformatora w stanie obciążenia (i zwarcia)
przedstawia się bez transformatora idealnego po sprowadzeniu wielkości strony
8
wtórnej na stronę pierwotną (w postaci II). Przeliczenia wielkości strony wtórnej na
stronę pierwotną dokonuje się korzystając z pojęcia przekładni transformatora
idealnego czy pojęcia równoznacznego – przekładni zwojowej transformatora N .
E
N
2
2

 1  1,
N
E N
(14)
gdzie:
N1 – liczba zwojów uzwojenia strony pierwotnej,
N2 – liczba zwojów uzwojenia strony wtórnej.
Wielkości strony wtórnej sprowadzone (przeliczone) na stronę pierwotną
oznaczymy z tzw. primem „’ ”. Ostatecznie otrzymamy:

E
1


E


E
sprowadzone napięcie E2 E2N, ponieważ: E
, czyli
2
2
1
E
2
ogólnie
2U
U
2
N,

sprowadzony prąd
I2 I2 

sprowadzoną rezystancję
2
R2 R2N
,
(17)
(15)
1
N ,
(16)

U

U
2
2 N
2

R



R

2
2
N
1

I
ponieważ:
,
2
I

2

N

sprowadzoną reaktancję
2
2 X2N
X
,
(18)

sprowadzoną impedancję
2R
2jX
2,
Z
(19)

sprowadzona moc
S2  S2 ,
(20)


U


I
IU

S
moc jest niezmiennicza ponieważ: S
,
2 2 2 2 2 2
sprowadzony kąt przesunięcia fazowego 2  2 ,
kąt
przesunięcia

fazowego


jest
niezmienniczy
(21)
ponieważ:


X
2
X
X
2N
2
2


arctg

arctg

arctg

.
2
2
2

R
R
R

2
2
2N
W zależności od potrzeb możemy wielkości sprowadzać w dowolnym kierunku ze
strony wtórnej na pierwotną lub z pierwotnej na wtórną. Schemat zastępczy jednej
fazy transformatora w stanie obciążenia, po sprowadzeniu strony wtórnej na stronę
pierwotną, przedstawiono na rysunku 1.6.
9
Rys. 1.6. Schemat zastępczy (1 faz.) transformatora w stanie obciążenia (postać II)
Uzyskanie schematu zastępczego transformatora w postaci połączonych obwodów
elektrycznych strony pierwotnej i strony wtórnej pozwala sporządzić wykres
wektorowy prądów oraz napięć i w dogodny sposób analizować pracę transformatora
w stanie obciążenia. Wykres wektorowy transformatora w stanie obciążenia
przedstawiono na rysunku 1.7.
Rys. 1.7. Wykres wektorowy (1 faz.) transformatora w stanie obciążenia
10
Budowę wykresu rozpoczynamy od wykreślenia napięcia U’2, czyli napięcia
odbiornika Z sprowadzonego na stronę pierwotną. Znajomość impedancji odbiornika
pozwala wykreślić prąd I’2 pod kątem 2  2 . Równoległe do wektora prądu I’2
kreślimy spadek napięcia U’R2 oraz prostopadle spadek U’X2. Koniec wektora U’X2
wyznacza siłę elektromotoryczną E1 = E’2. Równoległe z wektorem sem E1
wyznaczamy wektor prądu IFe (wynikający ze strat w rdzeniu), a prostopadle wektor
prądu Iμ (wynikający z magnesowania rdzenia – dla podkreślenia tego faktu
naniesiono linią przerywaną równoległy wektor strumienia głównego Φ ). Suma
wektorów prądów IFe i Iμ stanowi prąd I0, który dodany do wektora prądu I’2
pozwala na wykreślenie prądu I1 zasilającego transformator. Równoległe do wektora
prądu I1 kreślimy spadek napięcia UR1 oraz prostopadle spadek UX1. Koniec wektora
UX1 wyznacza żądane napięcie zasilania transformatora U1.
2.3. Stan zwarcia transformatora
Transformator znajduje się w stanie zwarcia, jeżeli uzwojenie pierwotne jest
zasilane napięciem U1 ze źródła, a obwód wtórny jest zwarty. W praktyce
eksploatacyjnej jest to stan awaryjny i powinien zostać w możliwie krótkim czasie
usunięty. W praktyce pomiarowej realizuje się stan zwarcia transformatora,
doprowadzając do jednego z uzwojeń (pierwotnego lub wtórnego) napięcie o takiej
wartości, żeby w uzwojeniu zasilanym otrzymać prąd znamionowy. W stanie zwarcia
napięcie na zaciskach zwartego uzwojenia jest równe zeru. Przez zwarte uzwojenie
płynie prąd, ale nie jest wydawana moc do odbiornika. Całkowita moc pobierana ze
źródła przez zwarty transformator pokrywa wyłącznie straty i w całości zamieniana
jest na ciepło. W stanie zwarcia pomiarowego przy obniżonym napięciu zasilania
pomija
się
straty
mocy w
rdzeniu
ΔP

ΔP

ΔP
, ponieważ
Fe
H
W
zgodnie
z zależnościami (3) i (4) straty te, zależąc od kwadratu napięcia (indukcja
magnetyczna ma wartość wprost proporcjonalną do napięcia), stanowią ułamek
procenta strat znamionowych. Z analogicznego powodu pomija się również wartość
prądu magnesującego Iμ , będącego rzędu kilku promili [4] prądu pobieranego
w stanie zwarcia (czyli prądu znamionowego). Uwzględniając powyższe, schemat
zastępczy i wykres wektorowy transformatora w stanie zwarcia przedstawiono na
rysunku 1.8.
11
Rys. 1.8. Schemat zastępczy i wykres wektorowy (1 faz.) transformatora w stanie zwarcia
Wobec równości prądów I1 = I’2 dla przedstawionego na rys. 1.8. schematu
równanie Kirchhoffa przyjmie postać:




U

U

U

U

U

R

I

jX

I

j
X

I

R

I
1
1
1
1 (22)
1
R1
X1
X2
R2
1
1R
2R
2








U

R

R

j
X

X

I

Z

I
1
Z
1
1
12
1R
2R
lub
(23)
gdzie:
2
RZR
R
1
– rezystancja zwarciowa,
2
X
X
X
Z
1
– reaktancja zwarciowa,
Z
R
jX
Z
Z
Z – impedancja zwarciowa.
Przy zwartym jednym uzwojeniu transformatora zasilamy drugie uzwojenie
napięciem UZ (napięcie zwarcia) o takiej wartości, żeby przez uzwojenie zasilane
płynął prąd znamionowy IN. Z pomiarów mocy (jednej fazy) PZ i napięcia UZ oraz
znajomości prądu znamionowego IN można wyznaczyć:

straty mocy w uzwojeniach (tzw. straty w miedzi) ΔP
Cu 3P
Z,

współczynnik mocy stanu zwarcia
P
cos

 Z ,
Z
U
I
Z N
(25)

impedancję zwarciową
ZZ 
UZ
,
IN
(26)

rezystancję zwarciową
ΔP
Cu P
Z
R
Z 2  2 ,
3I
I
N
N
(27)

reaktancję zwarciową
2
2
X
Z
R
Z
Z
Z,
(28)
(24)
oraz przybliżone wartości parametrów schematu zastępczego R1, R2, X1R, X2R
obliczane dla przekładni N przy założeniu R1  R2 i X1RX2R [4]:
12
R1 
RZ
,
2
R2 
R1
N2 ,
X1R 
(29)
(30)
XZ
,
2
(31)
X1R
2 .
(32)
X2R
N
Pomiary w stanie zwarcia łącznie z pomiarami w stanie jałowym umożliwiają
wyznaczenie przybliżonych wartości wszystkich elementów schematu zastępczego
transformatora.
3. Badania i pomiary
3.1. Określenie wielkości mierzonych
Wielkościami mierzonymi są: natężenie prądu przewodowego, moc czynna
i napięcia fazowe strony pierwotnej i wtórnej transformatora w stanie jałowym oraz
natężenia prądów przewodowych (strony pierwotnej i wtórnej), moc czynna i napięcie
strony pierwotnej transformatora w stanie zwarcia. Na podstawie danych
pomiarowych wyznacza się charakterystyki biegu jałowego i zwarcia oraz wartości
wszystkich elementów schematu zastępczego transformatora.
3.2. Wyznaczenie charakterystyk stanu jałowego transformatora
3.2.1. Schemat stanowiska
Stanowisko pomiarowe zasilane jest z regulowanego źródła prądu zmiennego
autotransformatora ATr. Układ pomiarowy przedstawiono na rysunku 1.9.
Rys. 1.9. Schemat układu pomiarowego do badań transformatora w stanie jałowym
13
3.2.2. Przebieg ćwiczenia
1. Zaznajomić się z danymi umieszczonymi na tabliczce znamionowej badanego
transformatora (dane znamionowe należy umieścić w sprawozdaniu).
2. Zmierzyć rezystancje wszystkich faz stron pierwotnej i wtórnej badanego
transformatora. Zastosować metodę techniczną – pomiary wykonać zgodnie
z zaleceniami prowadzącego zajęcia.
3. Zestawić układ pomiarowy wg rysunku 1.9. i zgłosić prowadzącemu gotowość
do zasilenia układu. Wyłącznik Q2 musi być rozwarty !
4. Dokonać pomiarów wartości mocy czynnej P0, natężenia prądu I0 oraz
napięcia U2 dla kolejno nastawianych (przy użyciu autotransformatora)
wartościach napięcia U1 (proponowane wartości napięć poda prowadzący
zajęcia – nie należy pominąć wartości napięcia znamionowego strony
pierwotnej!).
5. Wyniki pomiarów należy sukcesywnie notować w tabeli 1.1.
6. Po zakończeniu serii pomiarowej ustawić pokrętło autotransformatora
regulacyjnego na wartość minimalną i wyłączyć zasilanie. Wyłącznik Q1
ustawić w pozycji rozłączonej „0”.
7. Wypełnić część obliczeniową tabeli korzystając z zależności od (6) do (11).
UWAGA:
Wszelkie czynności związane z załączaniem zasilania oraz wyborem lub zmianą
zakresów pomiarowych przyrządów mogą być dokonane po uzyskaniu zgody i pod
nadzorem prowadzącego zajęcia. Układ pomiarowy nie jest separowany od sieci
zasilającej!
Tabela 1.1
L.p.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
U10(f)
V
Pomiary
I0(f)
U20(f)
A
V
P0(f)
W
U10(fm) U20(fm)
V
V
P0(3f)
W
Q0
var
S0
VA
Obliczenia
Φ0
I0%
----A
COSφ0
Iμ
A
IFe
A
υ
-
Xμ
Ω
RFe
Ω
3.3. Wyznaczenie charakterystyk zwarcia transformatora
3.3.1. Schemat stanowiska
Stanowisko pomiarowe zasilane jest z regulowanego źródła prądu zmiennego –
autotransformatora ATr. Układ pomiarowy przedstawiono na rysunku 2.0.
Rys. 2.0. Schemat układu pomiarowego do badań transformatora w stanie zwarcia
3.3.2. Przebieg ćwiczenia
1. Zestawić układ pomiarowy wg rysunku 2.0. i zgłosić prowadzącemu gotowość
do zasilenia układu.
2. Dokonać pomiarów wartości mocy czynnej PZ i natężeń prądów IZ dla kolejno
nastawianych (przy użyciu autotransformatora) wartościach napięcia U1
(proponowane wartości napięć poda prowadzący zajęcia – nie należy pominąć
wartości napięcia przy prądzie znamionowym strony pierwotnej i/lub
wtórnej!).
3. Wyniki pomiarów należy sukcesywnie notować w tabeli 1.2.
4. Po zakończeniu serii pomiarowej ustawić pokrętło autotransformatora
regulacyjnego na wartość minimalną i wyłączyć zasilanie oraz zlikwidować
stan zwarcia wyłącznikiem Q2 (!).
5. Wypełnić część obliczeniową tabeli, korzystając z zależności od (25) do (28)
i od (31) do (32).
3
Tabela 1.2
L.p.
Pomiary
Uz(f) I1zw
I2zw
V
A
A
Pz
W
Uz(mf) Uz%
V
v
ΔPFe
W
Obliczenia
φ
COSφ z
-
Zz
Ω
Rz
Ω
Xz
Ω
1
2
3
4
5
6
7
8
9
10
11
12
13
14
4. Opracowanie wyników pomiarów
Na podstawie wyników pomiarów należy:
1. Wykreślić charakterystyki stanu jałowego transformatora I0, P0, U2, cos0 ,
0 ,  , IFe, Iµ, RFe, Xµ w funkcji napięcia zasilającego U1 (wszystkie
charakterystyki umieszczone na jednym wykresie powinny różnić się od siebie
kolorem i/lub charakterem linii i opisem).
2. Wykreślić charakterystyki stanu zwarcia transformatora I Z1,IZ2, PZ, cos Z ,  Z ,
RZ, ZZ, XZ w funkcji napięcia zasilającego U1 (wszystkie charakterystyki
umieszczone na jednym wykresie powinny różnić się od siebie kolorem i/lub
charakterem linii i opisem ).
3. Narysować pełny schemat zastępczy transformatora (jak dla stanu obciążenia)
i podać na schemacie wartości wyznaczonych parametrów:
a) R1, R2
– z pomiarów w stanie zwarcia dla prądu znamionowego oraz
dla porównania (w nawiasie) z pomiarów bezpośrednich
(punkt 3.2.2.),
b) X1R, X2R – z pomiarów w stanie zwarcia dla prądu znamionowego,
c) RFe, Xµ – z pomiarów w stanie jałowym dla napięcia znamionowego.
4. Wyznaczyć wartości:
4
a) przekładni transformatora –
,
b) napięcia zwarcia
– uZ%,
c) prąd jałowy
– i0%,
d) strat mocy w rdzeniu
– ΔPFe,
e) strat mocy w uzwojeniu
– ΔPCu.
5. Sprawozdanie
Sprawozdanie powinno zawierać:
1. Stronę tytułową (nazwę ćwiczenia, numer sekcji, nazwiska i imiona
ćwiczących oraz datę wykonania ćwiczenia).
2. Dane znamionowe badanego transformatora.
3. Schematy układów pomiarowych.
4. Tabele wyników pomiarowych wraz z obliczeniami.
5. Charakterystyki podanych (w punkcie 4. - Opracowanie wyników pomiarów)
zależności.
6. Schemat zastępczy transformatora wraz z wartościami wymienionych
(w punkcie 4. - Opracowanie wyników pomiarów) parametrów.
7. Uwagi i wnioski (dotyczące przebiegu charakterystyk, ich odstępstw od
przebiegów teoretycznych, wartości wyznaczonych parametrów schematu
zastępczego, rozbieżności pomiędzy przybliżonymi wartościami rezystancji
uzwojeń obliczonymi dla stanu zwarcia a ich wartościami zmierzonymi itp.).
5
LITERATURA wymieniona zgodnie ze skryptem [2]
1. Praca zbiorowa: Elektrotechnika i elektronika dla nieelektryków. WNT,
Warszawa 1995.
2. Cholewicki T.: Elektrotechnika teoretyczna, tom I. WNT, Warszawa 1973.
3. Horowitz P., Hill W.: Sztuka elektroniki, tomy I i II. WKiŁ, Warszawa 1996.
4. Plamitzer A. M.: Maszyny elektryczne. WNT, Warszawa 1970.
5. Lebson S.: Podstawy miernictwa elektrycznego. WNT, Warszawa 1970.
6. Praca zbiorowa: Poradnik inżyniera elektryka, tom I. WNT, Warszawa 1996.
7. Wyrażanie niepewności pomiaru. Przewodnik. GUM, Warszawa 1995.
8. Krykowski K.: Energoelektronika. Wydawnictwo Politechniki Śląskiej, Gliwice
1998.
9. Rajchert F., Sitnik A., Stępień J.: Tyrystory i ich zastosowania. WKiŁ, Warszawa
1980.
10. Tietze U., Schenk Ch.: Układy półprzewodnikowe. WNT, Warszawa 1987.
11. Meyer K.: Poradnik elektryka. Ośrodek Doradztwa i Doskonalenia Kadr, Gdańsk
1998.
12. Gruza L., Krzeczyński A., Lipski S., Manczyk S., Niestępski S., Nowak A.,
Nowak Z., Wolski A.: Poradnik montera elektryka. WNT, Warszawa 2007.