Instrumenty pochodne

Matematyka finansowa i ubezpieczeniowa - 9
100
Instrumenty pochodne - opcje
80
60
40
20
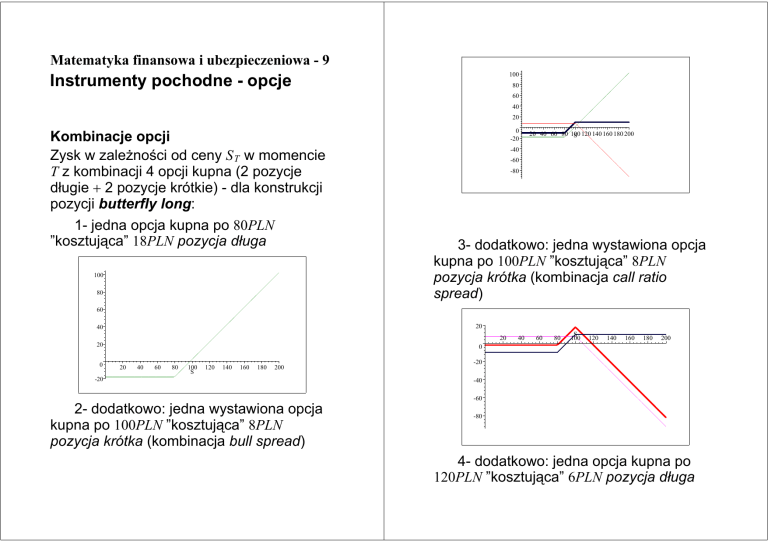
Kombinacje opcji
Zysk w zaleŜności od ceny S T w momencie
T z kombinacji 4 opcji kupna (2 pozycje
długie + 2 pozycje krótkie) - dla konstrukcji
pozycji butterfly long:
1- jedna opcja kupna po 80PLN
”kosztująca” 18PLN pozycja długa
100
80
0
-20
20 40 60 80 100
S 120 140 160 180 200
-40
-60
-80
3- dodatkowo: jedna wystawiona opcja
kupna po 100PLN ”kosztująca” 8PLN
pozycja krótka (kombinacja call ratio
spread)
60
40
20
20
0
20
0
20
40
60
80
100
S
120
140
160
180
200
-20
40
60
80
S
100
120
140
160
180
200
-20
-40
-60
2- dodatkowo: jedna wystawiona opcja
kupna po 100PLN ”kosztująca” 8PLN
pozycja krótka (kombinacja bull spread)
-80
4- dodatkowo: jedna opcja kupna po
120PLN ”kosztująca” 6PLN pozycja długa
(kombinacja butterfly)
S gt
↗p
60
40
St
20
20
40
60
S 120 140 160 180 200
80 100
↘ 1−p
0
-20
S dt
-40
-60
-80
Dwumianowy model wyceny
instrumentów pochodnych. Model
Coxa-Rossa-Rubinsteina
ZałóŜmy, Ŝe papier bazowy o cenie S t w
chwili t moŜe w momencie t + Δt kosztować:
S t+Δt
=
S gt z prawdopodobieństwem
p
S dt z prawdopodobieństwem 1 − p
tj. zmiana ceny następuje wg schematu na
drzewku:
ZałóŜmy, Ŝe roczne oprocentowanie lokat
(obligacji) wynosi r i niech 1 + r = e δ (δ −
roczna stopa ciągła). Przyjmujemy, Ŝe:
S dt ≤ e δΔt S t ≤ S gt
gdyŜ w przypadku przeciwnym moŜliwy by
był tzw. arbitraŜ.
Wartość f t+Δt = fS t+Δt  instrumentu
pochodnego na ten papier w momencie
t + Δt jest zaleŜna od ceny papieru
bazowego S t+Δt w momencie t + Δt :
f t+Δt
=
f gt z prawdopodobieństwem
p
f dt z prawdopodobieństwem 1 − p
Problem polega na ustaleniu
”sprawiedliwej” wartości f t instrumentu
pochodnego w momencie t
f gt
↗p
?f t
↘ 1−p
f dt
RozwaŜmy ”replikę” instrumentu
pochodnego, tzn. portfel A składający się z:
α jednostek papieru bazowego,
β jednostek obligacji
utworzony w momencie t. Jego wartość w
momencie t wynosi
V A t = αS t + βL t
gdzie L t cena jednej obligacji w momencie
t.
W momencie t + Δt wartość portfela A
wynosi
V A t + Δt = αS t+Δt + βL t+Δt =
αS gt + βL t e δΔt z pr.
=
p
αS dt + βL t e δΔt z pr. 1 − p
Ustalmy przy jakich α, β wartość portfela A
w momencie t + Δt jest taka sama jak
wartość instrumentu pochodnego, tzn.
rozwiąŜmy ze względu na α, β układ równań
αS gt + βL t e δΔt = f gt
αS dt + βL t e δΔt = f dt
Otrzymujemy:
α=
β=
f gt −f dt
S gt −S dt
S gt f dt −S dt f gt
L t S gt −S dt
e −δΔt
Skoro portfel A z tak dobranymi α, β
zapewnia w momencie t + Δt to samo co
instrument pochodny, to takŜe w momencie
t winien być wart tyle samo (w przeciwnym
wypadku moŜna wykonać arbitraŜ).
Zatem
f gt − f dt
S gt f dt − S dt f gt −δΔt
f t = V A t = g
St +
e Lt
S t − S dt
L t S gt − S dt 
= e −δΔt
=e
−δΔt
= e −δΔt
=e
−δΔt
g
δΔt f t
e
S gt
−
−
f dt
S dt
St +
S gt f dt
g
S t
−
−
S dt f gt
S dt 
e δΔt S t f gt − e δΔt S t f dt + S gt f dt − S dt f gt
S gt − S dt
g
g
e δΔt S t − S dt f t + S t − e δΔt S t f dt
S gt − S dt
Odnotujmy, Ŝe poniewaŜ S dt ≤ e δΔt S t ≤ S gt to
e δΔt S t − S dt
0≤q=
≤1
S gt − S dt
więc o q moŜna myśleć jak o nowym
(niezaleŜnym od p) prawdopodobieństwie,
tzw. prawdopodobieństwie arbitraŜowym
(nowa miara martyngałowa).
e δΔt S t − S dt g S gt − e δΔt S t d
ft +
ft
S gt − S dt
S gt − S dt
Dla opcji kupna z terminem wykonania T i
ceną rozliczenia X mamy więc (dla okresu
t, t + Δt = T − Δt, T):
f t = e −δΔt q ⋅ maxS gt − X, 0 + 1 − q ⋅ maxS dt − X, 0
q=
czyli
e δΔt S t − S dt
S gt − S dt
f t = e −δΔt q ⋅ f gt + 1 − q ⋅ f dt 
gdzie
q=
e
δΔt
S t − S dt
S gt − S dt
.
Gdy załoŜymy, Ŝe
S gt = S t ⋅ u, S dt = S t ⋅ l, u > 1, l ≤ 1 to
f t = e −δΔt q ⋅ maxS t u − X, 0 + 1 − q ⋅ maxS t l − X, 0
q=
e δΔt S t − S dt
S gt − S dt
Zadanie. Wyliczyć f t = f T−2Δt zakładając
schemat zmian cen papieru bazowego w
momentach
t = T − 2Δt, t + Δt = T − Δt, t + 2Δt = T
Przy załoŜeniu, Ŝe okres czasu t, T jest
podzielony na n podokresów
i
 i−1
n T − t, n T − t, i = 1, 2, . . . , n długości
Δt = 1n T, a zmiany cen są modelowane na
n −okresowym drzewku dwuminaowym,
którego pojedyńczym ogniwem jest
Si ⋅u
n
↗p
S gg
t
S ni
↗
↘ 1−p
S gt
↗
Si ⋅d
n
↘
S dg
t
St
↘
=
↗
S gd
t
gdzie S ni = St + ni T − t otrzymujemy
(przez indukcję) wzór na cenę opcji
c t = C t = cS t , t = S t Ψa, n, q ′  − Xe −δT−t Φa, n, q
S dt
n
↘
= e −nδΔt
S dd
t
∑
j=0
n
j
q j 1 − q n−j max0, u j d n−j S t − X
δΔt
q = e − d , q ′ = e −δΔt uq
u−d
ln S tXd n
a = 1+
ln ud
n
Φa, n, q = Q∑  n,i ≥ a
i=1
Uwaga. Przy odpowiednich załoŜeniach, z
powyŜszego wzoru otrzymujemy w granicy
(n  ∞) formułę Blacka-Scholesa:
c t = C t = cS t , t = S t Φd − Xe −δT−t Φd − σ T − t ,