Wykład VII
Układy trójfazowe
Układ napięć generatora
Rodzaje połączeń obwodów trój fazowych
Układ trójkątny faz odbiornika i generatora
Pomiar mocy w układach trójfazowych
Definicja układu trójfazowego
• Układem trójfazowym nazywamy układ trzech obwodów
elektrycznych, w których istnieją trzy źródła napięć
sinusoidalnych o jednakowej częstotliwości, przesunięte
względem siebie o określony kąt fazowy i wytworzone w
jednym generatorze zwanym generatorem trójfazowym.
Poszczególne obwody generatora trójfazowego nazywać
będziemy fazami i oznaczać literami A, B, C lub kolejnymi
cyframi 1, 2, 3.
Układ napięć generatora
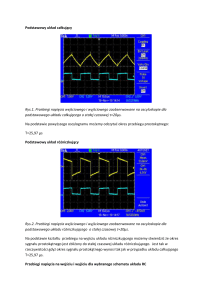
Rys. 1. Układ napięć źródłowych generatora symetrycznego
o kolejności zgodnej
•
•
Przykład połączenia 3 faz generatora w jeden układ gwiazdowy przedstawiony jest na
rysunku obok rys. 1.
Punkt wspólny wszystkich trzech faz generatora oznaczony jest cyfrą 0. Poszczególnym
napięciom fazowym przypisuje się wskaźniki A, B, C lub w przypadku oznaczenia
liczbowego cyfry 1, 2, 3. Układ napięć źródłowych generatora trójfazowego nazywa się
układem symetrycznym, jeśli napięcia kolejnych faz są przesunięte względem siebie
o kąt a amplitudy ich są sobie równe. Wartości chwilowe poszczególnych napięć
fazowych układu symetrycznego można zapisać w postaci.
Rys. 2. Wzór układu napięć źródłowych generatora
symetrycznego o kolejności zgodnej
Na rys. 3. przedstawiono przebiegi czasowe napięć
trójfazowych przy kącie początkowym ψ równym
zeru. Napięcia zmieniają się sinusoidalnie, zatem
występują regularne przesunięcia o kąt między
poszczególnymi sinusoidami.
Rys. 3. Przebiegi czasowe
napięć trójfazowych
Rys. 4. Wartości zespolone napięć
fazowych
Wobec sinusoidalnej postaci wymuszeń
w analizie układów trójfazowych stosuje
się metodę symboliczną. Zgodnie z nią
napięcia sinusoidalne zastępuje się ich
postacią zespoloną, która dla przyjętych
funkcji sinusoidalnych może być
zapisana jak na rys. 4.
Punkt wspólny napięć, odpowiadający punktowi
połączenia faz generatora oznaczony jest cyfrą 0. Na
końcach napięć fazowych zaznaczone są fazy (A, B, C).
Rys. 5. Wykres wektorowy napięć
trójfazowych generatora
Wirowanie faz
•
•
Napięcie fazowe generatora jest napięciem między
punktem końcowym wektora a punktem zerowym.
Wirowanie faz (zmiana pozycji wektora w czasie) w
generatorze trójfazowym odbywa się w przyjętym
układzie współrzędnych przeciwnie do ruchu
wskazówek zegara.
Rys. 6. Wektory napięć
trójfazowych wirujące w czasie
Oprócz napięć fazowych wyróżnia się również układy napięć
także liniowymi, czyli napięć panujących między
poszczególnych faz. Przy trzech napięciach fazowych
międzyfazowe określone wzorami: E E E
AB
•
A
B
E BC
międzyfazowych, zwanych
punktami zewnętrznymi
występują trzy napięcia
ECA EC E A
E B EC
Z definicji napięć międzyfazowych wynika, że niezależnie od symetrii
ich suma jest zawsze równa zeru, gdyż wszystkie napięcia tworzą
trójkąt zamknięty. Na rysunku 7 pokazano układ napięć
międzyfazowych generatora trójfazowego. Indeks symbolu EAB
oznacza, że strzałka wektora napięcia na wykresie jest skierowana
w stronę pierwszego wskaźnika (u nas litera A).
Rys. 7. Układ napięć międzyfazowych na tle napięć fazowych
Połączenia trójfazowe generatora i odbiornika
•
Układ napięć fazowych generatora może być połączony bądź w gwiazdę, bądź
w trójkąt. Schemat obu połączeń jest przedstawiony na rys. 8
Rys. 8. Połączenia faz generatora
trójfazowego w: a) gwiazdę,
b) trójkąt
•
Przy połączeniu trójkątnym generatora odbiornik jest zasilany
napięciem międzyfazowym trójprzewodowym. Przy połączeniu
generatora w gwiazdę, napięcie zasilające jest napięciem
fazowym, a liczba przewodów może być równa trzy lub cztery
(przy czterech przewodach zasilających jednym z nich jest
przewód zerowy, zwany również przewodem neutralnym). W
układzie trójfazowym, odbiornik zawiera również trzy fazy, przy
czym może być on połączony w gwiazdę lub w trójkąt. Oba
sposoby połączenia odbiornika przedstawione są na rys. 9.
Rys. 9. Odbiornik trójfazowy połączony w: a) gwiazdę, b) trójkąt
Rodzaje połączeń obwodów trójfazowych
•
W zależności od sposobu połączenia generatora i odbiornika, w układach
trójfazowych można wyróżnić cztery rodzaje połączeń. Są to:
1.
2.
3.
4.
•
generator i odbiornik połączone w gwiazdę (układ gwiazdowy),
generator i odbiornik połączone w trójkąt (układ trójkątny),
generator połączony w gwiazdę, a odbiornik w trójkąt,
generator połączony w trójkąt, a odbiornik w gwiazdę.
Z punktu widzenia metodyki analizy obwodów istotne są tylko dwa pierwsze
rodzaje połączeń. Dwa pozostałe są wtórne względem pierwszych i nie
wnoszą nowych elementów do metody analizy.
Układ gwiazdowy faz generatora i odbiornika
• Rozpatrzmy układ połączeń gwiazdowych odbiornika i generatora (gwiazdagwiazda) z oznaczeniami prądów i napięć przedstawionymi na rys. 10.
Rys. 10. Układ trójfazowy gwiazdowy
• Punkt 0 oznacza punkt wspólny faz generatora. Punkt N jest punktem
wspólnym impedancji fazowych odbiornika. Zakładamy symetrię napięć
fazowych generatora i dowolne wartości impedancji odbiornika. Przyjmijmy do
analizy układ czteroprzewodowy z impedancją przewodu zerowego równą.
Wartość impedancji może być dowolna, w szczególności zerowa (bezpośrednie
zwarcie punktów wspólnych generatora i odbiornika) lub nieskończona (układ
trójprzewodowy bez przewodu zerowego). Napięcie między punktem zerowym
odbiornika i generatora oznaczymy przez UN i będziemy nazywać napięciem
niezrównoważenia.
Analiza połączenia gwiazdowego obwodu
•
•
,
,
•
•
•
Układ napięć trójfazowych odbiornika tworzą napięcia na poszczególnych jego fazach,
czyli UA, UB, UC. W efekcie w obwodzie trójfazowym o połączeniu gwiazda-gwiazda
wyróżnia się dwa układy napięć trójfazowych gwiazdowych: generatora EA, EB, EC
i odbiornika UA, UB, UC.
W celu obliczenia prądów w obwodzie należy wyznaczyć układ napięć
odbiornikowych. Najlepiej dokonać tego wyznaczając napięcie UN.
Zastosujemy metodę potencjałów węzłowych przy założeniu, że punkt 0 jest węzłem
odniesienia, a poszukiwany potencjał węzłowy jest równy UN.
Zgodnie z metodą potencjałów węzłowych otrzymuje się: Z1 Z1 Z1 U EZ EZ EZ
Jeżeli oznaczymy:
A
A
A
A
B
C
A
B
C
n
oraz
to możemy zapisać równanie w następującej postaci:
Un
E A YA EB YB EC YC
YA YB YC YN
Wyznaczenie wartości napięcia UN pozwala obliczyć wartości napięć odbiornikowych.
Z prawa napięciowego Kirchhoffa zapisanego dla trzech oczek w obwodzie wynika:
U A EA U N
U B EB U N
U C EC U N
Analiza połączenia gwiazdowego obwodu
•
Przy znanych wartościach admitancji odbiornika, do obliczenia prądu stosuje się prawo
Ohma. Mianowicie
I A YA U A
I B YB U B
I C YC U C
I N YN U N
•
•
•
Suma prądów w węźle N jest równa zeru, zatem: I A I B I C I N
Moce wydzielone w odbiorniku trójfazowym oblicza się jako sumę mocy wydzielonych
w poszczególnych fazach odbiornika, czyli
S A PA jQ A U A I *A
S B PB jQB U B I B*
SC PC jQC U C I C*
Moc wydzielona na impedancji przewodu zerowego oznacza moc strat i wynosi
S N PN jQN U N I N*
•
Otrzymane wyniki można zinterpretować na wykresie wektorowym prądów i napięć
w obwodzie
.
Wykres wektorowy prądów i napięć dla przypadku obciążenia
niesymetrycznego
Rys. 11. Wykres wektorowy prądów
i napięć obwodu trójfazowego przy
obciążeniu niesymetrycznym
•
• Na rysunku widoczne są dwie gwiazdy napięć
fazowych: generatora o środku w punkcie 0
i odbiornika o środku w punkcie N.
• Dla obu gwiazd obowiązuje jeden trójkąt
napięć międzyfazowych.
• Przesunięcie potencjału punktu N względem 0
(napięcie UN różne od zera) jest
spowodowane niesymetrią odbiornika.
W pracy układu trójfazowego gwiazdowego można wyróżnić kilka
szczególnych przypadków:
1. odbiornik symetryczny z dowolną wartością impedancji przewodu
zerowego,
2. odbiornik niesymetryczny przy zwartym przewodzie zerowym,
3. zwarcie fazy odbiornika przy przerwie w przewodzie zerowym.
Odbiornik symetryczny
• W przypadku symetrii obciążenia, impedancje wszystkich faz odbiornika
Z A Z B ZC
YA YB YC
• Po uwzględnieniu tych równości
Un
E A YA EB YB EC YC
0
YA YB YC YN
• Ze względu na symetrię napięć generatora suma jego napięć fazowych jest
równa zeru, stąd napięcie niezrównoważenia UN w przypadku symetrii jest
zerowe.
• Oznacza to, że gwiazdy napięć odbiornikowych i generatorowych pokrywają
się.
• Prądy fazowe w tym przypadku wyznacza się więc prosto, na podstawie układu
napięć generatora, bez potrzeby obliczania napięcia niezrównoważenia UN:
I A E A YA
I B E B YB
I C EC YC
• Wobec
równości
admitancji
poszczególnych faz, suma prądów
fazowych wynosi:
I N I A I B IC Y ( E A EB EC ) 0
ze względu na zerowanie się sumy napięć
fazowych generatora.
• Prąd w przewodzie zerowym nie płynie,
niezależnie od wartości impedancji ZN
tego przewodu.
Rys. 12. . Wykres wektorowy prądów i napięć
w układzie trójfazowym symetrycznym
• Na rys. 12 przedstawiono wykres wektorowy prądów i napięć w układzie
trójfazowym symetrycznym.
• Wszystkie prądy i napięcia tworzą układ symetryczny o jednakowych
amplitudach i jednakowych przesunięciach poszczególnych wektorów
względem siebie.
• W praktyce najczęściej jest stosowany odbiornik symetryczny. Przykładami
takich odbiorników są silniki elektryczne trójfazowe czy piece grzejne
trójfazowe (zwykle o dużej mocy).
Odbiornik niesymetryczny przy zwartym
przewodzie zerowym
• Znaczne uproszczenia występują w analizie, jeśli punkt 0 i N układu
trójfazowego są połączone bezimpedancyjnie (ZN=0). W takim przypadku
napięcie niezrównoważenia UN=0, niezależnie od symetrii impedancji
odbiornika.
• Prądy fazowe są wówczas określane bezpośrednio na podstawie układu
napięć generatorowych
I A E A YA
I B E B YB
I C EC YC
• W przypadku odbiornika niesymetrycznego suma tych prądów jest różna
od zera
I N I A I B IC
• Wykres wektorowy prądów i napięć w układzie trójfazowym
niesymetrycznym przy zwarciu bezimpedancyjnym punktów wspólnych
odbiornika i generatora jest przedstawiony na rys. 13
Rys. 13. . . Wykres wektorowy prądów i napięć w układzie trójfazowym przy ZN=0
Układ trójkątny faz odbiornika i generatora
•
Schemat elektryczny połączeń elementów obwodu trójfazowego z odbiornikiem
i generatorem połączonymi w trójkąt (układ trójkąt-trójkąt) przedstawiono na rys. 14.
Rys. 14. Układ trójfazowy trójkątny
•
Napięcia odbiornika:
• Prądy odbiornika:
U AB E AB
I AB YAB E AB
U BC E BC
I BC YBC E BC
U CA ECA
I CA YCA ECAB
• Prądy liniowe:
I A I AB I CA
I B I BC I AB
I C I CA I BC
Pomiar mocy czynnej w układzie czteroprzewodowym
• Schemat połączenia trójkątnego i gwiazdowego impedancji przedstawiony
jest na rys. 15.
Rys. 15. Układy połączeń impedancji Z odbiornika symetrycznego w: a) trójkąt, b) gwiazdę
• Moc układu gwizdowego
P3
Uf
Z
2
cos ( )
• Moc układu trójkatnego
P3
( 3 U f )2
Z
cos ( ) 9
Uf
Z
2
cos ( )