Ćwiczenie 105

Ćwiczenie 108
Temat: POMIAR CIEPŁA WŁAŚCIWEGO CIECZY METODĄ DWÓCH
KALORYMETRÓW.
I. Literatura:
1. Ćwiczenia laboratoryjne z fizyki. Praca zbiorowa pod redakcją Tadeusza
Rewaja.
II. Tematy teoretyczne:
Pojęcie ciepła, temperatury i energii wewnętrznej, ciepło właściwe i molowe
ciepło właściwe, przemiany fazowe, zasada bilansu cieplnego.
III. Metoda pomiarowa:
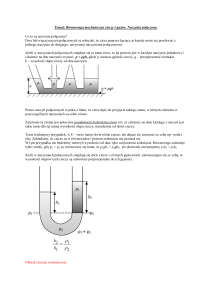
Dwie spirale z drutu o jednakowym oporze elektrycznym są podłączone
szeregowo, dzięki czemu, w obu spiralach wydziela się tyle samo ciepła w
jednostce czasu. Ta sama ilość ciepła ogrzewa wodę w jednym kalorymetrze i inną
ciecz (np. olej silikonowy) w drugim. Ponieważ ciecze mają różne ciepła właściwe,
przyrost temperatury tych cieczy będzie inny.
Ciepło właściwe nieznanej cieczy można obliczyć układając bilans cieplny.
Zmierzyć należy masy cieczy i kalorymetrów oraz przyrosty temperatur.
IV. Zestaw przyrządów:
Dwa kalorymetry ze spiralami o jednakowym oporze, dwa termometry o
dokładności 0,1oC (wypożyczyć w pok. 619 pod zastaw legitymacji lub innego
dokumentu), źródło prądu zmiennego 9V
V. Kolejność czynności:
a) Otworzyć oba kalorymetry, nie rozłączając przewodów i odstawić je na bok.
Wyjąć metalowe naczynia z izolującej obudowy.
Uwaga: Nie wylewać oleju. Naczynia zostały wcześniej zważone. Masa
naczynia, w którym jest olej wynosi m 1k=39,8801g, a masa naczynia, w
którym jest woda wynosi m 2k =39,8201g.
b) Sprawdzić, czy poziomy oleju i wody nie są niższe niż poziom zaznaczony
wewnątrz naczynia. W razie potrzeby dolać wody destylowanej z butli, a o
uzupełnienie poziomu oleju poprosić w pok. 619.
c) Wyznaczyć masę wody (m2 ) i badanej cieczy (m1). (waga dostępna jest w
pok. 619)
d) Złożyć z powrotem oba kalorymetry zwracając uwagę, aby grzałki
przeznaczonej do wody nie włożyć do oleju i na odwrót.
e) Włożyć termometry w uchwyty w kalorymetrach i włączyć je (sprawdzić czy
termometry wskazują temperaturę w oC i w razie potrzeby skorygować to).
Zamieszać ciecze w kalorymetrach za pomocą wystających z obudowy
metalowych uchwytów mieszadeł, odczekać kilkanaście sekund i odczytać
temperatury oleju i wody (t1, t2).
f) Włączyć zasilanie grzałek (wyłącznik z diodą świecącą na przewodzie
podłączonym do kalorymetrów)
g) Gdy temperatura w naczyniu z olejem wzrośnie o ok. 5-8oC , zamieszać
ponownie ciecze i odczytać temperatury w obu naczyniach .
(Uwaga: w celu
termometrze-
kontroli temperatury co 2-3 minuty wcisnąć przycisk „ON_HOLD” na
wtedy dopiero termometr dokonuje pomiaru)
h) Czynności z punktu „g” powtórzyć jeszcze dwukrotnie dla coraz wyższych
temperatur (temperaturę końcową poprzedniego pomiaru potraktować jako
temperaturę początkową dla pomiaru następnego)
i) Wyłączyć zasilanie grzałek.
Tabela pomiarów i wyników:
Nr
m1
m2
[kg] [kg]
mk1
[kg]
mk2
t1
t2
t1’
t2’
[kg]
o
o
o
o
[ C] [ C] [ C] [ C]
cx
Δ cx
 J 
 kg  K 


 J 
 kg  K 


1
2
3
Wartość średnia i jej niepewność
t1, t2 temperatury początkowe, a t'1, t'2 temperatury końcowe w kalorymetrach,
t1  t1'  t1 t 2  t 2'  t 2
mk1=39,8801g -masa tego kalorymetru, w którym jest olej silikonowy,
mk2 =39,8201g- masa tego kalorymetru, w którym jest woda,
ck1=ck2=ck= 896 J/kg.K – ciepło właściwe kalorymetrów (aluminium)
c2= 4175 ±1 J/kg.K – ciepło właściwe wody ( w zakresie 25 oC -40 oC )
j) Wyliczyć ciepło właściwe nieznanej cieczy z wzoru:


m

c

m

c


t
c
2
2
k
2
k
2m
k
1
k
c


x
m


t
m
1
1
1
Dla ułatwienia pracy warto najpierw obliczyć wartości cząstkowe. W tym celu
należy wyliczyć wartości następujących wyrażeń:
A  m2  c2 ;
B  mk 2  c k ;
C
t 2
;
t1
D  mk 1  c k
wówczas wzór przyjmie postać:
cx 
1
 A  B C  D
m1
k) Wyliczyć niepewności całkowite ciepła właściwego dla każdego pomiaru.
W obliczeniach uwzględnić tylko niepewności wielkości mierzonych
samodzielnie, przyjmując, że niepewności podane w niniejszej instrukcji są tak
niewielkie, iż można je pominąć. Ostatecznie uwzględnimy tylko niepewności
pomiaru mas wody i badanej cieczy oraz różnic temperatur w obu cieczach.
Przy takich uproszczeniach wzór na niepewność całkowitą pojedyńczego
pomiaru przyjmie postać:
2
2
 c   u (m ) 
 c
u (c x )   x    B 1    x
3 
 m1  
 m2
2
2
2
2
2
  u B (t 2 ) 
  
 
3



 1
  u B (m1 ) 
 1  A  B   t 2   u B (t1 ) 
c
  u (m ) 

   2  C    B 2    2 
  
 2   A  B C  D   
  
m1
3 
3 
3 
 m1
 

 m1
 
 t1
 
2

2
  u B (m2 ) 
 c   u (t ) 
 c
  
   x    B 1    x
3 
3 
 
 t1  
 t 2
2
2
2
2
Uwaga: Przy pierwszym obliczaniu można zauważyć, które człony
powyższego wzoru mają znikomy wpływ na wielkość niepewności
maksymalnej Δcx i przy następnych obliczeniach ich nie uwzględniać, co
uprości nieco żmudne rachunki.
j) obliczyć średnie ciepło właściwe c x i jego niepewność c x (w badanym
zakresie temperatur różnice ciepła właściwego są pomijalnie małe w porównaniu
z niepewnościami pomiarowymi). Wyniki wpisać do tabeli.
2