Klasa 5. Figury na płaszczyźnie

Klasa 5. Figury na płaszczyźnie
Astr. 1/6
.................................................................................
imię i nazwisko
.....................
.........................
klasa
data
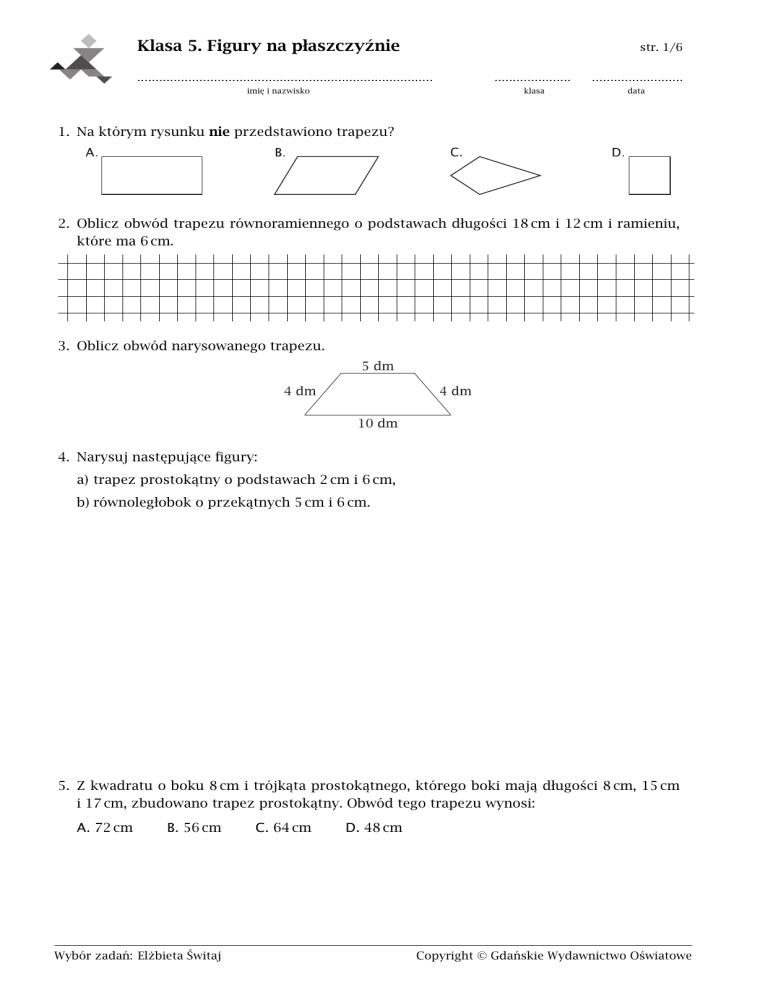
1. Na którym rysunku nie przedstawiono trapezu?
2. Oblicz obwód trapezu równoramiennego o podstawach długości 18 cm i 12 cm i ramieniu,
które ma 6 cm.
3. Oblicz obwód narysowanego trapezu.
4. Narysuj następujące figury:
a) trapez prostokątny o podstawach 2 cm i 6 cm,
b) równoległobok o przekątnych 5 cm i 6 cm.
5. Z kwadratu o boku 8 cm i trójkąta prostokątnego, którego boki mają długości 8 cm, 15 cm
i 17 cm, zbudowano trapez prostokątny. Obwód tego trapezu wynosi:
A. 72 cm
B. 56 cm
Wybór zadań: Elżbieta Świtaj
C. 64 cm
D. 48 cm
Copyright © Gdańskie Wydawnictwo Oświatowe
Astr. 2/6
6. Trapez 𝐴𝐵𝐶𝐷 jest równoramienny, a czworokąt
𝐴𝐵𝐹𝐸 to kwadrat o boku 6 cm. Odcinek 𝐷𝐸 ma długość 8 cm, a odcinek 𝐴𝐷 – 10 cm.
Oceń prawdziwość poniższych zdań. Wstaw znak X
w odpowiednią kratkę.
Podstawa 𝐶𝐷 jest dwa razy dłuższa niż ramię tego trapezu.
prawda
fałsz
Obwód trapezu wynosi 34 cm.
prawda
fałsz
7. Narysuj trapez równoramienny prostokątny, którego jedna z podstaw ma długość 6 cm, a ramię 5 cm.
8. Ramię trapezu równoramiennego i krótsza podstawa mają taką samą długość. Dłuższa podstawa jest 2 razy dłuższa od ramienia. Jaką długość mają boki tego trapezu, jeżeli jego
obwód wynosi 30 cm?
9. Z dwóch jednakowych trapezów prostokątnych zbudowano trapez równoramienny, który
nie jest prostokątem, a następnie prostokąt. Oceń prawdziwość zdań. Wstaw znak X w odpowiednią kratkę.
Dłuższa podstawa trapezu prostokątnego jest dwa razy
krótsza od podstawy trapezu równoramiennego.
prawda
fałsz
Prostokąt i trapez równoramienny mają jednakowe obwody.
prawda
fałsz
Wybór zadań: Elżbieta Świtaj
Copyright © Gdańskie Wydawnictwo Oświatowe
Astr. 3/6
10. Trapez 𝐴𝐵𝐶𝐷 jest równoramienny. Kąt 𝛼 ma miarę:
D
C
100
A
A. 100∘
B. 40∘
C. 260∘
B
D. 80∘
11. Wpisz brakujące miary kątów w trapezie.
130
47
12. Kąt ostry w trapezie prostokątnym ma 57∘. Oblicz i wypisz miary pozostałych kątów w tym
trapezie.
13. Jeden z kątów w trapezie równoramiennym ma 60∘. Oblicz i wypisz miary pozostałych kątów
w tym trapezie.
14. Uzupełnij zdania.
Jeżeli dwa kąty w trapezie mają miary 60∘ i 60∘, to taki czworokąt nazywamy trapezem
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ..
Jeżeli dwa kąty w trapezie mają miary 100∘ i 90∘, to taki czworokąt nazywamy trapezem
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ..
Wybór zadań: Elżbieta Świtaj
Copyright © Gdańskie Wydawnictwo Oświatowe
Astr. 4/6
15. Ustal miary kątów poniższych czworokątów:
a) trapezu prostokątnego
o kącie rozwartym 130∘
b) rombu, którego kąt ostry
ma miarę 40∘
c) równoległoboku, którego
kąt rozwarty ma miarę 120∘
𝛼 =............. 𝛾 =.............
𝛼 =............. 𝛾 =.............
𝛼 =............. 𝛾 =.............
𝛽 =............. 𝛿 =.............
𝛽 =............. 𝛿 =.............
𝛽 =............. 𝛿 =.............
16. Proste 𝑎 i 𝑏 są równoległe. Wpisz na rysunku miary kątów trapezu 𝐴𝐵𝐶𝐷.
C
D
a
135
b
70
B
A
17. Trójkąt 𝐴𝐶𝐷 jest trójkątem prostokątnym równoramiennym. Kąt 𝐴𝐶𝐵 jest o 15∘ większy
od kąta 𝐴𝐵𝐶.
Uzupełnij zdania:
Kąt 𝐴𝐵𝐶 ma miarę
. . . . . . . .
Kąt rozwarty trapezu 𝐴𝐵𝐶𝐷 jest o
tego trapezu.
. . . . . . . .
większy od kąta ostrego
18. Kąt rozwarty trapezu równoramiennego 𝐴𝐵𝐶𝐷 jest trzykrotnie większy od kąta ostrego.
Oblicz długość odcinka 𝐸𝐶, wiedząc, że podstawa 𝐴𝐵 jest o 3 cm dłuższa od podstawy 𝐶𝐷.
D
C
h
B
E
A
19. Podkreśl nazwy czworokątów, w których przekątne nie zawsze są równej długości.
równoległobok
Wybór zadań: Elżbieta Świtaj
trapez
romb
kwadrat
prostokąt
Copyright © Gdańskie Wydawnictwo Oświatowe
Astr. 5/6
20. Długość boku rombu jest równa 4 cm, boku kwadratu – 4 cm, a prostokąt ma wymiary
3 cm × 5 cm. Wynika z tego, że:
A. najmniejszy jest obwód prostokąta
B. obwody wszystkich trzech czworokątów są jednakowe
C. największy jest obwód kwadratu
D. największy jest obwód prostokąta
21. Znajdź na rysunku i wypisz:
a) cztery trapezy, które nie są równoległobokami
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
b) cztery równoległoboki
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
22. Oceń prawdziwość poniższych zdań. Wstaw znak X w odpowiednią kratkę.
Romb, którego przekątne mają długości 7 cm i 4 cm, nie
jest kwadratem.
prawda
fałsz
Istnieje trapez prostokątny, który ma dokładnie trzy
kąty proste.
prawda
fałsz
23. Trapez zbudowano z pięciu trójkątów równobocznych o boku 6 cm. Oceń, czy poniższe zdania są prawdziwe, czy fałszywe. Wstaw znak X w odpowiednią kratkę.
Obwód tego trapezu wynosi 42 cm.
prawda
fałsz
Kąt rozwarty tego trapezu ma 120∘.
prawda
fałsz
24. Która z wymienionych figur ma największy obwód?
A. Romb, którego bok ma długość 4 cm.
B. Równoległobok, którego boki mają długości 4 cm i 5 cm.
C. Trapez równoramienny, w którym jedna podstawa i ramię mają po 2 cm, a druga podstawa
ma długość 5 cm.
D. Czworokąt, którego boki mają długości 2 cm, 3 cm, 4 cm i 5 cm.
25. Zaznacz własności, które może mieć dany czworokąt. Wpisz + lub − .
własności
równoległobok
prostokąt
romb
trapez
kwadrat
przekątne przecinające się pod kątem 140∘
przekątne o długościach 15 cm i 11 cm
kąty o mierze 100∘, 100∘, 80∘, 80∘
Wybór zadań: Elżbieta Świtaj
Copyright © Gdańskie Wydawnictwo Oświatowe
Astr. 6/6
26. Czworokąt 𝐴𝐵𝐸𝐹 jest rombem, a czworokąt 𝐵𝐶𝐷𝐸 – trapezem równoramiennym. Oblicz
miary kątów czworokąta 𝐴𝐶𝐷𝐹.
F
E
D
40°
A
B
C
D
27. Ustal, czy prawdziwe jest zdanie:
Obwód prostokąta 𝐵𝐸𝐹𝐷 jest o 10 cm większy od sumy długości przekątnych rombu 𝐴𝐵𝐶𝐷.
Wybierz poprawny początek odpowiedzi i jedno jej
uzasadnienie.
A
5 cm
B
F
C
E
obwód prostokąta jest równy sumie długości przekątnych rombu.
TAK,
NIE,
ponieważ
obwód prostokąta jest o 5 cm większy od sumy długości przekątnych rombu.
przekątna 𝐴𝐶 ma długość równą sumie długości równoległych
do niej boków prostokąta.
Wybór zadań: Elżbieta Świtaj
Copyright © Gdańskie Wydawnictwo Oświatowe