Lekcja 20

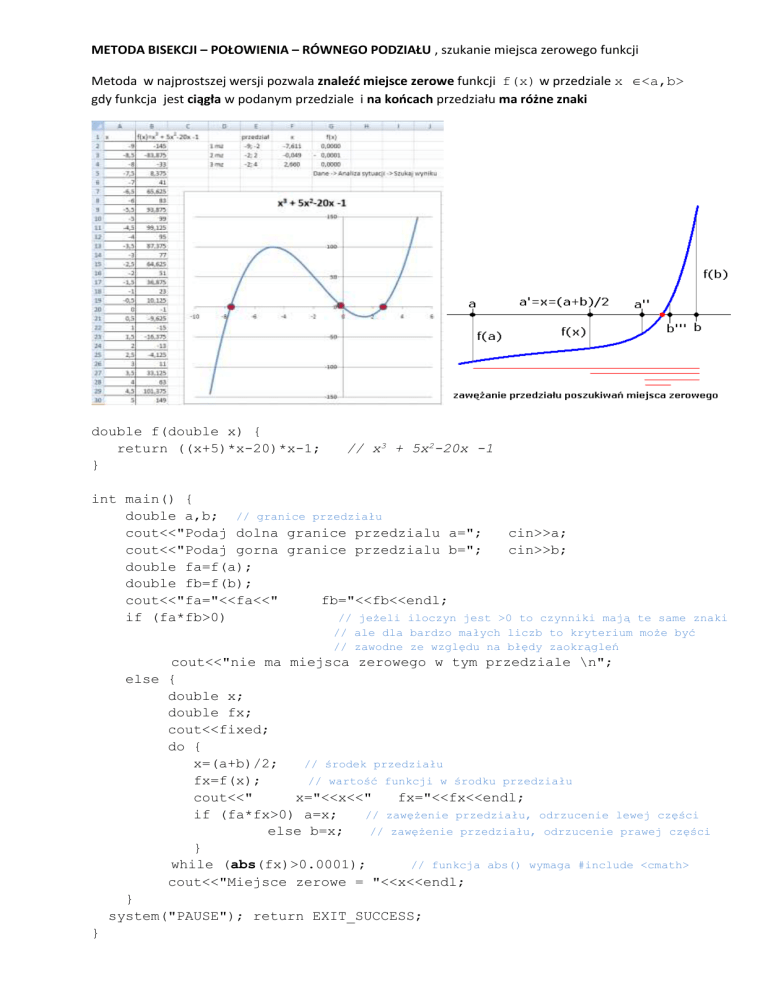
METODA BISEKCJI – POŁOWIENIA – RÓWNEGO PODZIAŁU , szukanie miejsca zerowego funkcji
Metoda w najprostszej wersji pozwala znaleźć miejsce zerowe funkcji f(x) w przedziale x <a,b>
gdy funkcja jest ciągła w podanym przedziale i na końcach przedziału ma różne znaki
double f(double x) {
return ((x+5)*x-20)*x-1;
}
// x3 + 5x2-20x -1
int main() {
double a,b; // granice przedziału
cout<<"Podaj dolna granice przedzialu a=";
cin>>a;
cout<<"Podaj gorna granice przedzialu b=";
cin>>b;
double fa=f(a);
double fb=f(b);
cout<<"fa="<<fa<<"
fb="<<fb<<endl;
if (fa*fb>0)
// jeżeli iloczyn jest >0 to czynniki mają te same znaki
// ale dla bardzo małych liczb to kryterium może być
// zawodne ze względu na błędy zaokrągleń
cout<<"nie ma miejsca zerowego w tym przedziale \n";
else {
double x;
double fx;
cout<<fixed;
do {
x=(a+b)/2;
// środek przedziału
fx=f(x);
// wartość funkcji w środku przedziału
cout<<"
x="<<x<<"
fx="<<fx<<endl;
if (fa*fx>0) a=x;
// zawężenie przedziału, odrzucenie lewej części
else b=x;
// zawężenie przedziału, odrzucenie prawej części
}
while (abs(fx)>0.0001);
// funkcja abs() wymaga #include <cmath>
cout<<"Miejsce zerowe = "<<x<<endl;
}
system("PAUSE"); return EXIT_SUCCESS;
}
SCHEMAT HORNERA – to sposób obliczania wartości wielomianu f(x)dla danej wartości x,
przy
minimalnej liczbie mnożeń. Schemat ten wiązany jest z nazwiskiem Wiliama Hornera (pocz. XIXw) , był jednak
znany wcześniej Newtonowi, a nawet matematykom chińskim w XII wieku.
f(x) = an*xn+an-1*xn-1+an-2*xn-2 + … +a2*x2+a1*x+a0
Obliczanie f(x) na podstawie pełnego wyrażenia, gdzie xn = x*x*x*…*x, oznacza konieczność
wykonania wielu operacji mnożenia, bardzo czasochłonnych dla procesora:
(n-1)+ (n-2) +…+2+1=
n * ( n  1)
operacji mnożenia.
2
Zamiast jawnie wyznaczać kolejne potęgi zmiennej : x2, x3, … xn, można f(x) obliczać tak:
f(x) = ((((an*x+an-1)*x+an-2)*x+ …
+a2)*x + a1)*x + a0
co wymaga tylko n operacji mnożenia!
Pamiętaj że tablice są indeksowane od 0. Wspólczynniki ai można umieszczać w tablicy w porządku :
 od wyrazu an do a0,
A[0]=an , … , A[n]=a0, wówczas pętla i będzie przebiegać od n do 0
 odwrotnie, od wyrazu a0 do an, , A[0]=a0 , … , A[n]=an, wówczas petla i będzie przebiegać od 0 do n
Przykład: Masz wielomian 6-go stopnia: f(x) =x6+2x5+3x4+4x3+5x2+6x+7.
Współczynniki można umieścić w tablicy int A[7]={1,2,3,4,5,6,7}.
Kod C++ obliczania wartości tego wielomianu dla danej float x, wykorzystujący minimalną liczbę
operacji mnożenia (według schematu Hornera):
float x=0.7;
const int n=6; // stopień wielomianu
int A[n+1] = {1,2, 3, 4, 5, 6, 7}; // indeksy w tablicy A są liczone od 0
// indeks i= 0
1
2
3
4
5
6
float f=A[0];
for (int i=1; i<=n; i++) f=f*x+A[i];
cout<<w<<endl;
Zastosowanie do obliczania wartości dziesiętnej liczby, podanej w systemie liczbowym o podstawie x.
Jeśli współczynniki a0, a1, …, an są liczbami całkowitymi z zakresu <0,x> to wielomian można
potraktować jako wyrażenie, które zwraca wartość dziesiętną liczby danej w systemie liczbowym o podstawie
x, na przykład gdy x=2 mamy liczbę binarną:
101101BIN =
1*25+0*24+1*23+1*22+0*21+1*20
Program który pobiera łancuchy binarne (do 100 cyfr) i zwraca równoważną każdemu liczbę dziesiętną:
string s;
int n;
int A[100];
while (s!="0") {
cout<<"\nPodaj liczbe binarna "; cin>>s;
n=s.length();
// konwersja znaków (cyfr) na liczby (współczynniki wielomianu)
for (int i=0; i<n; i++) A[i]=s[i]-48;
int d=A[0];
for (int i=1; i<n; i++) d=d*2+A[i];
cout<<"dziesietnie = "<<d<<endl;
// schemat Hornera
}
Zadanie:
W pliku podstawy.txt znajdują się liczby zapisane w różnych systemach liczbowych. W każdej linii pliku są
dwie wartości całkowite:
pierwsza oznacza podstawę systemu liczbowego
druga oznacza daną liczbę zapisana w tym systemie
Twój program ma:
obliczyć sumę wszystkich danych liczb zapisanych w różnych systemach liczbowych
wyświetlić tę sumę w postaci dziesiętnej i w postaci szesnastkowej
znaleźć wśród danych liczb wszystkie liczby piewsze
// zwraca i-tą cyfrę łańcucha s
int cyfra(string s, int i) {
char c=s[i];
int main() {
if (c>=65) return c-55;
ifstream we("podstawy.txt");
int p; // podstawa systemu liczbowego
else return c-48;
string s; // dana liczba jako łańcuch znaków
}
int suma=0;
// suma wszystkich liczb
bool pierwsza(int x) {
while (we>>p) {
bool tak=true;
we>>s;
for (int i=2; i<=sqrt(x); i++)
int n=s.length();
if (x%i==0) {tak=false; break;}
int w=cyfra(s,0);
return tak;
for (int i=1; i<n; i++)
}
w=w*p+cyfra(s,i);
cout<<p<<" "<<s<<" dziesietnie = "<<w<<endl;
suma+=w;
if (pierwsza(w)) cout<<"liczba pierwsza\n";
}
we.close();
cout<<"\nsuma="<<suma<<" hex="<<hex<<suma<<endl;
system("PAUSE");
return EXIT_SUCCESS;
}
Zastosowanie schematu Hornera do dzielenia wielomianu przez jednomian (x-p) gdzie pQ
Q = zbiór liczb wymiernych
Szukamy wspólczynników funkcji g(x)takiej że
f(x) = (x-p)*g(x) + reszta
an*xn+an-1*xn-1+…+a2*x2+a1*x+a0 = (x-p)*(bn-1*xn-1+…+b2*x2+b1*x+b0 )+ reszta
Uwaga: w jednomianie (x-p) współczynnik przy x musi być zawsze równy 1 !
Po obliczeniu iloczynu nawiasów prawej strony i porównaniu współczynników przy tych samych potęgach x
otrzymuje się wyrażenia wyznaczające kolejne wspólczynniki bi
bn-1 = an
bn-2 = an-1 + p*bn-1
bi
= ai+1 + p*bi+1
b0
= a1 + p*b1
reszta= a0 + p*b0
Zadanie: Znajdz wszystkie pierwiastki całkowite wielomianu x5+8x4-48x3-382x2-209x+630
z przedziału x od -10 do 10.
Gdy znajdziesz pierwiastek p, wyświetl wielomian będący wynikiem dzielenia wielomianu wyjsciowego przez
(x-p) i dalej szukaj już pierwiastków tego nowego wielomianu
const int n=6; // rozmiar tablicy (o 1 więszy niż stopień wielomianu
int A[n] = {630, -209, -382, -48, 8, 1};
// tym razem zapisuję
//współczynniki w tablicy w odwrotnym porządku, od a0 do an
int B[n-1];
int reszta;
int stopien=n-1;
//
for (int p=-10; p<=10; p++) {
int p=7;
// najpierw sprawdzam dla wybranej wartości pierwiastka p=7
// następnie uogólnię to na pętlę po p<-10,10>
B[stopien-1]=A[stopien];
for (int i=stopien-2; i>=0; i--) B[i]=A[i+1]+p*B[i+1];
reszta=A[0]+p*B[0];
cout<<p<<"
reszta="<<reszta;
if (reszta==0) {
cout<<" pierwiastek\n";
stopien--;
cout<<"Pozostaje wielomian ";
for (int j=stopien; j>=0; j--) cout<<"+"<<B[j]<<"*x^"<<j<<" ";
for (int j=stopien; j>=0; j--) A[j]=B[j];
}
cout<<"\n\n";
// }
Wyniki: (możesz to sprawdzić na http://wolframalfa.com )
Wielomian x5+8x4-48x3-382x2-209x+630 = (x+5)*(x-7)*(x-1)*(x+2)*(x+9), ma pierwiastki: -9, -5, -2, 1, 7