9. Planimetria - teoria

9. PLANIMETRIA
9.1. Okrąg i koło
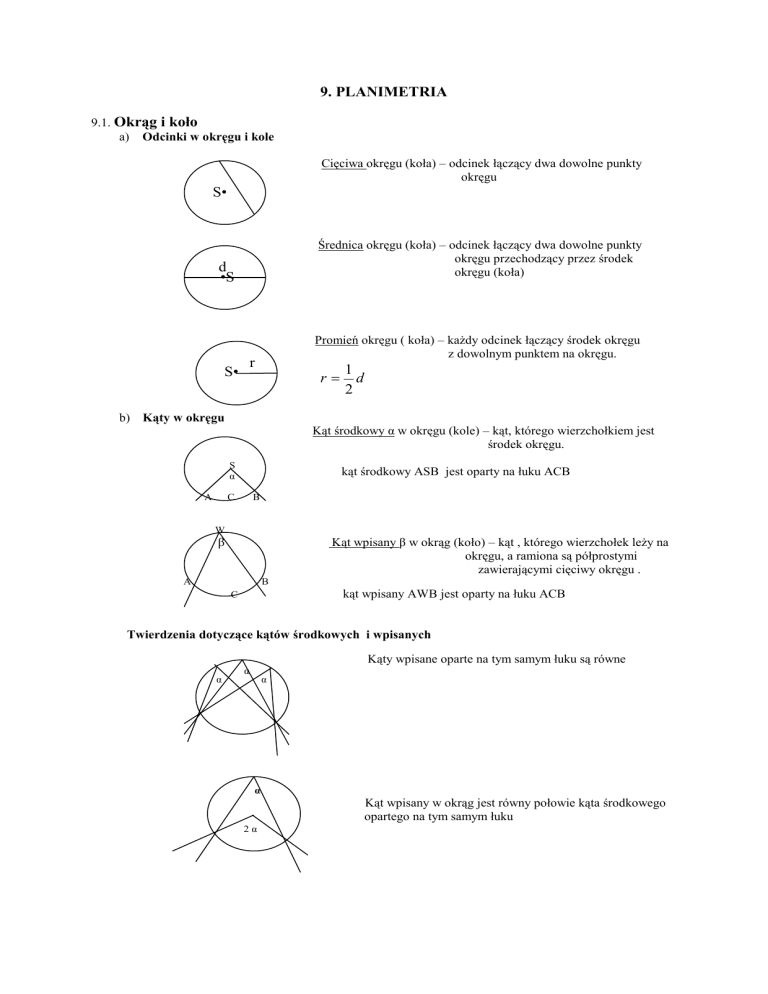
a) Odcinki w okręgu i kole
Cięciwa okręgu (koła) – odcinek łączący dwa dowolne punkty
okręgu
S•
Średnica okręgu (koła) – odcinek łączący dwa dowolne punkty
okręgu przechodzący przez środek
okręgu (koła)
d
•S
Promień okręgu ( koła) – kaŜdy odcinek łączący środek okręgu
z dowolnym punktem na okręgu.
r
S•
r=
1
d
2
b) Kąty w okręgu
Kąt środkowy α w okręgu (kole) – kąt, którego wierzchołkiem jest
środek okręgu.
S
α
A
kąt środkowy ASB jest oparty na łuku ACB
C
B
W
β
Kąt wpisany β w okrąg (koło) – kąt , którego wierzchołek leŜy na
okręgu, a ramiona są półprostymi
zawierającymi cięciwy okręgu .
A
B
kąt wpisany AWB jest oparty na łuku ACB
C
Twierdzenia dotyczące kątów środkowych i wpisanych
Kąty wpisane oparte na tym samym łuku są równe
α
α
α
α
Kąt wpisany w okrąg jest równy połowie kąta środkowego
opartego na tym samym łuku
2α
c)
Pole i obwód koła
P = π ⋅r2
Wzór na pole koła
Wzór na obwód koła ( długość okręgu)
r
Ob = 2π ⋅ r
d) Pole wycinka koła i długość łuku
r
Wzór na pole wycinka koła
P=
Wzór na długość łuku
l=
α
l
e)
α
360°
α
360°
π ⋅r2
2π ⋅ r
Styczna do okręgu
Styczna do okręgu jest prostopadła do promienia poprowadzonego
do punktu styczności
S
•
·
9.2. Trójkąty
a) Klasyfikacja trójkątów
Podział trójkątów ze względu na boki
róŜnoboczny
prostokątny
b
b
b
c
c
a
b
·
a
c
a
b
b
b
a
b) Suma kątów wewnętrznych trójkąta jest równa
180°
a
a
a
·
równoboczny
a
a
b
rozwartokątny
Podział trójkątów ze względu na kąty
ostrokątny
a
równoramienny
c)
Odcinki i linie w trójkącie
wysokość trójkąta h – odcinek łączący wierzchołek trójkąta z
przeciwległym bokiem, prostopadły do
niego.
h
r
s
d
dwusieczna kąta d – półprosta , która dzieli kąt na pół
·
·
S
S- środek boku
środkowa trójkąta r – odcinek łączący wierzchołek trójkąta
ze środkiem przeciwległego boku.
Twierdzenie o środkowych trójkąta: Środkowe trójkąta przecinają się w punkcie,
który nazywamy środkiem cięŜkości trójkąta. Punkt ten dzieli
kaŜdą ze środkowych w stosunku 2 : 1 licząc do wierzchołków.
symetralna boku trójkąta s
– prosta prostopadła do boku
i przechodząca przez jego środek
d) Przystawanie trójkątów
C
α
c
b
Cechy przystawania trójkątów
β
Cecha BBB : < ABC ≡< A' B ' C ' ⇔ a = a '∧b = b'∧c = c '
Cecha BKB : < ABC ≡< A' B ' C ' ⇔ a = a '∧b = b'∧γ = γ '
γ
A
a
B
Cecha KBK :
< ABC ≡< A' B ' C ' ⇔ a = a '∧ β = β '∧γ = γ '
C’
α‘
c’
b’
Przystające trójkąty - trójkąty, które mają równe boki i kąty
β‘
γ’
A’
e)
a‘
B’
Podobieństwo trójkątów
C
c
Cechy podobieństwa trójkątów
α
A β
a b c
= =
a ' b' c'
a b
Cecha BKB : < ABC ~ < A' B ' C ' ⇔
= ∧γ = γ'
a ' b'
Cecha KKK: < ABC ~ < A' B ' C ' ⇔ α = α '∧ β = β '
b
a
Cecha BBB:
γ
B
< ABC ~ < A' B ' C ' ⇔
C’
α'
c’
β’
A’
Podobne trójkąty - trójkąty, które mają równe kąty
i proporcjonalne boki
b’
γ’
a’
skala podobieństwa trójkąta ABC do trójkąta A’B’C’:
B’
Jeśli k jest skalą podobieństwa trójkąta ABC do trójkąta A’B’C’ , to
PABC
= k2
PA' B 'C '
k=
a b c
= =
a ' b' c'
f)
Pole trójkąta
P=
1
a⋅h
2
P=
1
a ⋅ b ⋅ sin α
2
h
·
a
b
α
a
a
P=
b
p( p − a )( p − b )( p − c )
gdzie
p=
1
(a + b + c )
2
c
g) Okrąg wpisany w trójkąt
a
b
r
- środkiem okręgu wpisanego w trójkąt jest punkt przecięcia
dwusiecznych kątów wewnętrznych trójkąta.
- wzór na promień okręgu wpisanego w trójkąt
r=
c
2P
gdzie P – pole trójkąta
a+b+c
h) Okrąg opisany na trójkącie
- środkiem okręgu opisanego na trójkącie jest punkt przecięcia symetralnych boków trójkąta
S – środek okręgu
okrąg opisany na trójkącie
ostrokątnym
okrąg opisany na trójkącie
prostokątnym
okrąg opisany na trójkącie
rozwartokątnym
·
·S
·S
·S
γ
R
a
b
β
- wzory na promień okręgu opisanego na trójkącie
c
α
i)
R=
a ⋅b⋅c
4P
R=
a
b
c
=
=
2 sin α 2 sin β 2 sin γ
gdzie P – pole trójkąta
Trójkąt równoramienny
a- podstawa trójkąta
b- ramię trójkąta
kąty przy podstawie są równe,
wysokość dzieli podstawę na połowę
wysokość dzieli kąt między ramionami na połowę
b
b
α
α
a
j)
Trójkąt równoboczny
a
a
60
a
- w trójkącie równobocznym wszystkie kąty maja po 60° .
- w trójkącie równobocznym środkowe, symetralne, wysokości,
dwusieczne przecinają się w tym samym punkcie, który jest
jednocześnie promieniem okręgu wpisanego w ten trójkąt, jak i
okręgu opisanego na tym trójkącie.
a2 3
wzór na pole trójkąta równobocznego P =
4
wzór na wysokość trójkąta równobocznego
h
r
h=
a 3
2
wzory na promień okręgu wpisanego w trójkąt równoboczny
R
1
r= h
3
r=
a 3
6
wzory na promień okręgu opisanego na trójkącie równobocznym
R=
2
h
3
R=
a 3
3
k) Trójkąt prostokątny
a – przyprostokątna naprzeciw α
b- przyprostokątna przy α
c - przeciwprostokątna
c
a
·
α
b
- twierdzenie Pitagorasa
a2 + b2 = c2
- funkcje trygonometryczne kąta ostrego
a
b
ctgα =
b
a
1
- wzór na pole trójkąta prostokątnego: P = a ⋅ b
2
sin α =
a
c
cos α =
b
c
tgα =
- wzór na promień okręgu opisanego na trójkącie prostokątnym:
R=
1
c
2
9.3. Czworokąty
a) Klasyfikacja czworokątów
czworokąt wypukły
czworokąt niewypukły
trapezoid
trapez
równoległobok
deltoid
prostokąt
romb
kwadrat
b) Suma kątów wewnętrznych czworokąta jest równa 360°
c)
Trapez
b
δ
c
w trapezie przynamniej jedna para boków jest równoległa
a , b – podstawy trapezu
γ
h
d
α
β
c, d - ramiona trapezu
h – wysokość trapezu
α + δ = 180°
a
β + γ = 180°
b
`Odcinek łączący środki ramion jest równoległy do podstaw i
x
wyraŜa się wzorem
x=
a+b
2
a
a
Wzór na pole trapezu :
P=
1
(a + b ) ⋅ h
2
h
b
Trapez równoramienny
b
β
- kąty wewnętrzne trapezu równoramiennego przy tej samej
podstawie są równe,
- przekątne trapezu równoramiennego są równe i dzielą się
samym stosunku,
β
c
c
α
e
α
e
- wzór na e w trapezie równoramiennym: e
a
Trapez prostokątny
- wzór na e w trapezie prostokątnym : e
=
a −b
2
= a−b
b
h
h
c
·
e
a
d) Równoległobok
a
β
α
b
b
α
β
a
- w równoległoboku przeciwległe boki są równe
i równoległe,
- w równoległoboku przeciwległe kąty są równe,
- w równoległoboku α + β = 180°
- w równoległoboku przekątne przecinają się w połowie
Wzory na pole równoległoboku:
P = a⋅h
h
a
b
P = a ⋅ b ⋅ sin α
α
a
e)
Romb
a
β
- w rombie wszystkie boki są równe,
- w rombie przeciwległe kąty są równe,
- w rombie α + β = 180°
-
α
a
a
α
β
a
Przekątne w rombie:
- dzielą się na połowę,
- przecina ją się pod kątem prostym,
··
1
d2
2
1
d1
2
1
β
2
1
α
2
r
- dzielą kąty wewnętrzne na połowę
Okrąg wpisany w romb:
- środek okręgu wpisanego w romb jest punktem przecięcia
przekątnych rombu
- wzór na promień okręgu wpisanego w romb
r=
Wzory na pole rombu
P = a⋅h
h
a
P = a 2 ⋅ sin α
a
α
a
d1
d2
P=
1
d1 ⋅ d 2
2
1
h
2
f)
Prostokąt
b
a
- przekątne w prostokącie są równe i dzielą się na połowy
- wzór na pole prostokąta:
P = a ⋅b
a
b
Okrąg opisany na prostokącie:
- środkiem okręgu opisanego na prostokącie jest punkt
przecięcia przekątnych prostokąta
- wzór na promień okręgu opisanego na prostokącie
R
R=
1
d
2
d – przekątna prostokąta
g) Kwadrat
a
-
przekątne kwadratu są równe, przecinają się pod kątem prostym i
dzielą się na połowy
a
d
- wzór na przekątną kwadratu:
-
d =a 2
wzór na pole kwadratu:
P = a2
Okrąg wpisany w kwadrat i okrąg opisany na kwadracie
- punkt przecięcia przekątnych kwadratu jest środkiem okręgu
wpisanego w kwadrat i środkiem okręgu opisanego na
kwadracie.
- wzór na promień okręgu wpisanego w kwadrat :
R
r
r=
-
1
a
2
wzór na promień okręgu opisanego na kwadracie:
R=
1
d
2