Znajdowanie liczby najmniejszej

Przykład: znajdowanie liczby najmniejszej.
Wskazać najmniejszą spośród trzech różnych liczb: a, b, c.
Inne sformułowanie zadania:
Mając trzy różna liczby a,b,c, wyznaczyć liczbę m , tak aby
m =a lub m = b lub m = c, przy czym m ≤ a , m ≤ b , m ≤ c.
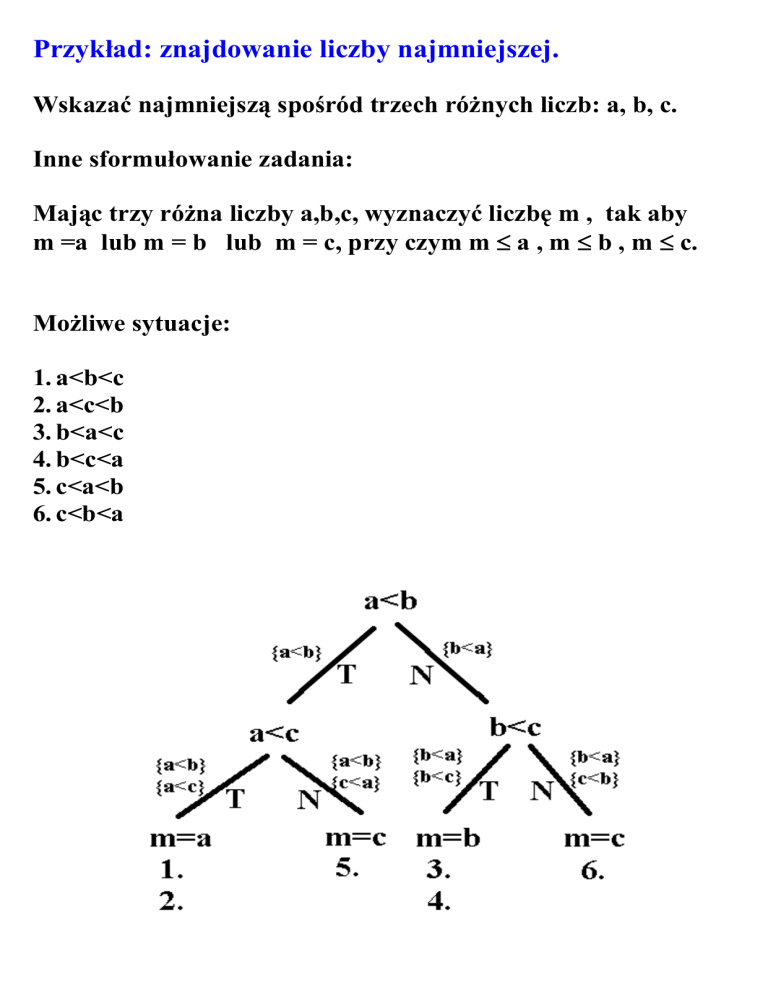
Możliwe sytuacje:
1. a<b<c
2. a<c<b
3. b<a<c
4. b<c<a
5. c<a<b
6. c<b<a
Maszyna różnicowa Charlesa Babbage’a
Kolejne kwadraty
Kolejne liczby nieparzyste
12 = 0 + 1 ←⎯⎯⎯ 1
22 = 1 + 3 ←⎯⎯⎯
3=1+2
32 = 4 + 5 ←⎯⎯⎯
5=3+2
42 = 9 + 7 ←⎯⎯⎯
7=5+2
Aby policzyć kwadrat kolejnej liczby należy:
1. Ustawić liczby 0, 1 i 2 jako wartości początkowe
2. Wykonać dwa dodawania
• Dodać 2 dla uzyskania następnej liczby nieparzystej
• Dodać wynik do poprzedniego kwadratu
Systemy liczenia:
System dziesiętny:
- cyfry:
0,1,2,3,4,5,6,7,8,9
- postać liczby:
Cn Cn-1 Cn-2 . . . C1 C0
- wartość liczby:
Cn*10n+Cn-1*10n-1+Cn-2*10n-2+ ...+C1*101+C0*100
System dwójkowy (binarny):
- cyfry:
0,1
- postać liczby:
Bn Bn-1 Bn-2 . . . B1 B0
- wartość liczby:
Bn*2n+Bn-1*2n-1+Bn-2*2n-2+ ...+B1*21+B0*20
Postać binarna liczby dziesiętnej:
(13) 10= 8+4+1= 1*23+1*22+1*20 = 1*23+1*22+0*21+1*20
(13) 2= 1101
(191)10
191:2=95 r 1
95:2=47 r 1
47:2=23 r 1
23:2=11 r 1
11:2=5 r 1
5:2=2
r1
2:2=1
r0
1:2=0
r1
↑
⏐
⏐
⏐
⏐
⏐
⏐
⏐
(191)2 = 10111111
Sumowanie
dziesiętne:
binarne:
7
111
+5
+101
12
1100
Maszyny podstawowe (bramki i sumatory):
Bramka NOT:
Input (A)
1
0
Output (B)
0
1
Bramka AND:
Input(A)
1
1
0
0
Input(B)
1
0
1
0
Output(C)
1
0
0
0
Bramka OR:
Input(A)
1
1
0
0
Input(B)
1
0
1
0
Output(C)
1
1
1
0
Bramka OR
Sumator dwójkowy jednopozycyjny:
Input(A)
0
0
0
1
1
0
1
1
Input(B)
0
0
1
0
1
1
0
1
Input(Z1)
0
1
0
0
0
1
1
1
Output(C)
0
Output(Z2)
0
1
0
0
1
1
1
Algorytm Euklidesa
Dane są dwie nieujemne liczby całkowite m , n . Liczba
k=NWD(m,n) jest największym wspólnym dzielnikiem m i n jeśli
dzieli m oraz n i jest największą liczbą o tej własności.
Algorytm Euklidesa znajduje największy wspólny podzielnik.
Załóżmy n ≥ m ⇒ n = q *m + r gdzie 0 ≤ r < m.
Stąd:
• Jeśli r = 0 to NWD(m,n)=m
Jeśli jedna z liczb dzieli drugą bez reszty to mniejsza z tych
liczb jest największym wspólnym dzielnikiem.
• Jeśli r ≠ 0 to r = n – q*m
Każda liczba dzieląca n i m dzieli także r ⇒
NWD(m,n)=NWD(r,m) przy czym zgodnie z punktem
pierwszym NWD(0,m) = m.
Rozważmy liczby n=48, m=46.
48=1*46+2
46=23*2+0
czyli NWD(46,48)=NWD(2,46)=NWD(0,2) = 2
Zależność n = q *m + r zapewnia, że możemy generować pary
liczb o tym samym największym wspólnym dzielniku, elementy
tych par tworzą malejący ciąg liczb naturalnych.
Ciąg ten jest skończony, na jego końcu otrzymujemy szukany
dzielnik.