Moc czynna, bierna i pozorna

Moc czynna, bierna i pozorna
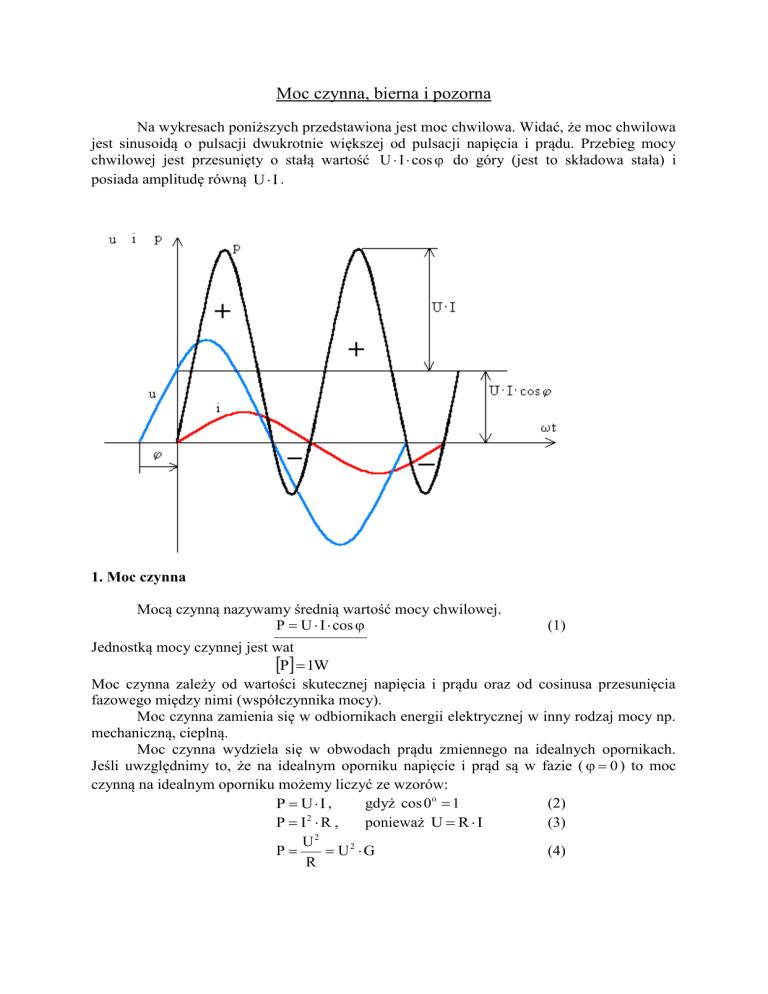
Na wykresach poniższych przedstawiona jest moc chwilowa. Widać, że moc chwilowa
jest sinusoidą o pulsacji dwukrotnie większej od pulsacji napięcia i prądu. Przebieg mocy
chwilowej jest przesunięty o stałą wartość U  I  cos  do góry (jest to składowa stała) i
posiada amplitudę równą U  I .
1. Moc czynna
Mocą czynną nazywamy średnią wartość mocy chwilowej.
P  U  I  cos 
(1)
Jednostką mocy czynnej jest wat
P  1W
Moc czynna zależy od wartości skutecznej napięcia i prądu oraz od cosinusa przesunięcia
fazowego między nimi (współczynnika mocy).
Moc czynna zamienia się w odbiornikach energii elektrycznej w inny rodzaj mocy np.
mechaniczną, cieplną.
Moc czynna wydziela się w obwodach prądu zmiennego na idealnych opornikach.
Jeśli uwzględnimy to, że na idealnym oporniku napięcie i prąd są w fazie (   0 ) to moc
czynną na idealnym oporniku możemy liczyć ze wzorów:
gdyż cos 0o  1
(2)
P  UI ,
2
ponieważ U  R  I
(3)
P  I R ,
2
U
(4)
P
 U2  G
R
2. Moc bierna
Moc bierna jest iloczynem wartości skutecznej napięcia, prądu i sinusa przesunięcia
fazowego między napięciem i prądem.
Q  U  I  sin 
(5)
Jednostką mocy biernej jest war.
Q  1var
Moc bierna nie może zamienić się w odbiornikach w inny rodzaj mocy. Moc ta
pulsuje między źródłem a odbiornikiem. Pobór mocy biernej przez odbiorniki jest
ograniczany (poprawa cos  ).
Moc bierną w obwodach prądu zmiennego pobierają tylko idealne cewki oraz idealne
kondensatory.
Jeśli uwzględnimy, że na idealnej cewce   90o a na idealnym kondensatorze
  90o możemy napisać następujące wzory na moc bierną.
(6)
QL  U  I
2
(7)
QL  I  X L
(8)
QC   U  I
Q C  I 2  X C
(9)
Q L - moc bierna na cewce
Q C - moc bierna na kondensatorze
Moc bierna na kondensatorze jest ujemna, ponieważ:
sin( 90o )  1
3. Moc pozorna
Moc pozorna jest iloczynem wartości skutecznej napięcia i prądu.
(10)
S  UI
Jednostką mocy pozornej jest woltamper.
S  1VA
Aby znaleźć związek między mocą czynną, bierną i pozorną obliczmy:
2
P 2  Q 2  ( U  I  cos ) 2  U  I  sin   ( U  I) 2 (cos 2   sin 2 )
Biorąc pod uwagę to, że S  U  I , oraz cos 2   sin 2   1 mamy
P 2  Q2  S2
Moc czynna, bierna i pozorna tworzą trójkąt prostokątny mocy.
(11)
Z trójkąta mocy wynikają następujące związki.
P 2  Q2  S2
Q
tg 
P
P  S  cos 
Q  S  sin 
4. Moc pozorna zespolona
Narysujmy trójkąt mocy na płaszczyźnie zespolonej.
Z rysunku widać, że moc pozorną
możemy potraktować jako liczbę
zespoloną i przedstawić ją w
postaci:
S  P  jQ  Se j
Tak przedstawioną moc nazywamy
mocą pozorną zespoloną.
Jej część rzeczywista (P) to moc
czynna, część urojona (Q) to moc
bierna, moduł (S) to moc pozorna a
argument (  ) to przesunięcie
fazowe między napięciem a
prądem.
Obliczmy teraz moc pozorną zespoloną.
S  P  jQ  UI cos   jUI sin   UI(cos   jsin )
S  U  I  e j  U  I  e j( u i )  Ue ju  Ie  ji
Jeśli uwzględnimy, że:
Ue ju  U

Ie  ji  I
Wzór na moc pozorną zespoloną przyjmuje postać:
(12)
S  U  I
Moc pozorna zespolona jest iloczynem wartości zespolonej napięcia oraz wartości zespolonej
sprzężonej prądu.
Zadanie
Oblicz moc czynną, bierną i pozorną pobieraną przez następujący dwójnik.
U=230V
R=30Ω
XL=60Ω
XC=100Ω
Rozwiązanie 1.
Obliczymy wartość skuteczną prądu płynącego przez dwójnik oraz przesunięcie
fazowe między napięciem a prądem. Następnie policzymy poszczególne moce.
Z  R 2  (XL  XC ) 2  302  (60  100) 2  50
X  X C 60  100
tg  L

 1,33
R
30
  53,13o
U 230
I 
 4,6A
Z 50
P  UI cos   230  4,6  cos(53,13o )  634,8W
Q  UI sin   230  4,6  sin( 53,13o )  846,4 var
S  UI  230  4,6  1058VA
Rozwiązanie 2.
Obliczymy moc pozorną zespoloną.
Z  R  j(X L  XC )  30  j(60  100)  (30  j40)
U
230
I 
 (2,76  j3,68)A
Z 30  j40

S  U  I  230  (2,76  j3,68)  634,8  j846,4  1058e j53,13 VA
P  634,8W
Q  846,4 var
S  1058VA
Rozwiązanie 3.
Obliczymy moc pobieraną przez każdy element obwodu.
Z  R 2  (XL  XC ) 2  302  (60  100) 2  50
U 230
I 
 4,6A
Z 50
P  I 2  R  4,62  30  634,8W
QL  I 2  X L  4,62  60  1269,6 var
Q C  I 2  X C  4,6 2 100  2116 var
Q  QL  QC  1269,6  2116  846,4 var
S  P 2  Q 2  634,82  (846,4) 2  1058VA
o