I. A) Opisz sens fizyczny zasad dynamiki Newtona oraz użytych do

Przykładowe zagadnienia do egzaminu z Fizyki dla 1. r. st. stacjonarnych I st. kierunku Inżynieria
Środowiska; sesja letnia r. ak. 2014/15. Wszystkie dane w treści zagadnień podano w SI.
Uwaga: Wszystkie odpowiedzi liczbowe, wyprowadzone lub wykorzystane wzory należy koniecznie
opatrzyć stosownymi komentarzami (wyjaśniając znaczenie użytych symboli), których brak zdyskwalifikuje
wyniki liczbowe, wyprowadzone lub wykorzystane wzory.
I. A) Opisz sens fizyczny zasad dynamiki Newtona oraz użytych do ich matematycznego zapisu wielkości
fizycznych podając ich jednostki miary. Przytoczyć i opisać sens fizyczny najogólniejszej postaci drugiej
zasady dynamiki oraz wyjaśnić jaki ma ona związek z zasadą zachowania pędu.
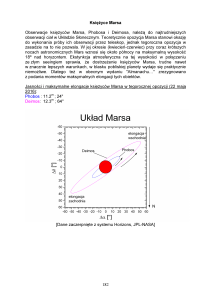
B) Na powierzchni Marsa (fotografia planety obok, ciśnienie na jego powierzchni ≈ 800 Pa = 0,008
ziemskiego ciśnienia atmosferycznego; planeta prawie nie ma atmosfery) rzucono pod
kątem 30o stopni do poziomu kulę o masie 0,2 kg z prędkością początkową o wartości
21 m/s. W trakcie ruchu na kulę działa stała siła F = (Fx; Fy; Fz) = (0,0; –0,74; 0,0) [N].
Składowe wektora siły F podano w prostokątnym układzie współrzędnych, którego osie
OX i OZ leżą w płaszczyźnie powierzchni Marsa, a oś OY jest skierowana do góry.
Wyznacz:
B1) Tor ruchu, tj. zależność y(x), gdzie y – wysokość nad powierzchną planety, x – odległość wyrzuconej
kuli mierzona po powierzchni Marsa od punktu wyrzutu będącego początkiem prostokątnego układu
współrzędnych.
B2) Czas wznoszenia się kuli.
B3) Wektor przyspieszenia całkowitego a kuli w dowolnym punkcie naszkicowanego toru ruchu; należy
przedstawić a graficznie na wykresie y(x) w trzech różnych punktach toru ruchu.
B4) Przyspieszenie styczne i normalne w najwyższym punkcie toru ruchu.
B5) Wartość pracy siły przyciągania marsjańskiego w trakcie trwania ruchu kuli.
B6) Niechaj p = (px; py; pz) będzie wektorem pędu wyrzuconej kuli. Wyjaśnij, dlaczego wartość składowej
poziomej wektora pędu jest stała, tj. px = const w trakcie ruchu, a składowa pionowa py ulega zmianom.
---------------------------------------------------------------------------------------------------------------------II. A) Zasady dynamiki Newtona. Opisz sens fizyczny tych zasad oraz znaczenie zastosowanych w tekście
odpowiedzi pojęć, symboli, wielkości fizycznych.
II.B) W sierpniu 2012 roku na powierzchni Marsa (fotografia planety
po lewej stronie) wylądował amerykański łazik Curiosity, z pokładu
którego wykonano wiele niezwykłych zdjęć przesłanych następnie na
Ziemię (fotografia po prawej stronie przedstawia wschód Słońca na tej
planecie, dzisiaj jest 17 XII 2014 r. doniesiono, ze stacja ta wykryła
metan w atmosferze Marsa). Ciśnienie atmosferyczne na powierzchni Marsa jest bardzo
niskie i wynosi około 800 Pa = 0,008 ziemskiego ciśnienia atmosferycznego, co oznacza, że planeta ta
praktycznie nie ma atmosfery.
B1) Z pokładu Curiosity wystrzelono pionowo do góry kulkę A o masie 0,03 kg z prędkością o wartości
12,4 m/s, która spadła po czasie 6,7 s. Wyznacz natężenie pola grawitacyjnego na powierzchni Marsa.
B2) Z podstawy łazika Curiosity przylegającej do powierzchni Marsa rzucono pod kątem 30o stopni do
powierzchni planety kulkę B o masie 0,02 kg z prędkością początkową o wartości 15 m/s.
B2.1) W prostokątnym układzie współrzędnych, którego osie OX i OY są równoległe do powierzchni
planety, a oś OZ – o dodatnim zwrocie w górę – jest prostopadła do powierzchni Marsa, podaj
wartości składowych wektora siły F = (Fx; Fy; Fz) działającej na kulkę w trakcie ruchu. Należy
skorzystać z wyników zadania B1).
1
B2.2) Wyznacz tor ruchu kulki, tj. zależność z(x), gdzie z – wysokość nad powierzchną planety, x –
odległość wyrzuconego ciała mierzona po powierzchni Marsa od punktu wyrzutu; założyć, że ciało
wyrzucono z początku prostokątnego układu współrzędnych. Naszkicuj tor ruchu i przedstaw na tym
wykresie wektor przyspieszenia całkowitego w 3 różnych, wybranych punktach toru.
B2.3) Oblicz czas wznoszenia się kulki B na wysokość maksymalną.
B2.4) Opisz sens fizyczny wektorów przyspieszenia stycznego i normalnego, wielkości występujących
w ruchu krzywoliniowym. Jaka jest wartość przyspieszenia normalnego w ruchu po prostej?
C) Masz do swojej dyspozycji płaską deskę, której powierzchni pokryta jest teflonem, miedziany sześcian,
płaski stół, kątomierz oraz tablicę wartości funkcji trygonometrycznych. Opisz i uzasadnij metodę
doświadczalnego wyznaczania, przy zastosowaniu wyżej określonych przyrządów i tablicy, statycznego
współczynnika tarcia miedź/teflon.
D) Jesteś opiekunką/opiekunem dziecka przebywającego na kuracji w zakładzie balneologiczny. „Twoje” dziecko ześlizguje się
z wysokości h po idealnie gładkiej powierzchni
do basenu z wodą, co ilustruje rysunek.
Dziecko wyskakuje ze zjeżdżalni będąc na
wysokości h/5 pod kątem Θ. Wyznacz
maksymalną wysokość y, na którą wzniesie się dziecko jako funkcję h i Θ.
E) Na ciało spadające pionowo w dół działa siła F oporu zależna od prędkości v, a jej wartość wynosi F = Cρv2S/2,
gdzie ρ = 1,3 kg/m2 – gęstość powietrza, S – pole przekroju prostopadłego ciała w stosunku do wektora prędkości, C
– współczynnik zależny od kształtu ciała. Piłeczka pingpongowa ma masę 2,5 g i promień 1,7 cm. Przyjmując, że C =
0,5 oblicz prędkość z jaką upuszczona swobodnie piłeczka będzie spadała ruchem jednostajnym prostoliniowym
(przyjmujemy, że powietrze jest nieruchome).
F) Przedstaw i opisz sens fizyczny II zasady dynamiki w nieinercjalnym układzie odniesienia. Jakie znasz
przejawy nieinercjalności układu odniesienia związanego z Ziemią?
--------------------------------------------------------------------------------------------------------------------III.Fizyka pola grawitacyjnego. Jakie wielkości fizyczne (skalarne i wektorowe) charakteryzują to pole?
Opisz znaczenie zastosowanych w tekście odpowiedzi pojęć, symboli, wielkości fizycznych.
A) Planeta Mars o promieniu RM = 3400 km ma masę M = 6,4·1023 kg i nie posiada praktycznie atmosfery
na powierzchni tej planety ciśnienie wynosi ≈ 800 Pa, co stanowi 8·10-3 ziemskiego ciśnienia atmosferycznego.
A1) Wyznacz natężenie pola grawitacyjnego na powierzchni Marsa przyjmując G = 7·10-11 N·m2/kg2.
A2) Na jaką wysokość wzniesie się ciało wyrzucone pionowo do góry z powierzchni Marsa
z prędkością 30 m/s?
A3) Jednym z naturalnych księżyców Marsa jest Fobos (fotografia obok), który
orbituje wokół Marsa po orbicie o promieniu 9400 km. W jakim czasie Fobos obiega
Marsa?
A4) Oblicz pierwszą i drugą prędkość kosmiczną dla Marsa.
A5) Oblicz średnią odległość Marsa od Słońca o masie MS = 2,0·1030 kg, wiedząc, że
średnia prędkość orbitalna Marsa to 24 km/s.
A6) Doba na Marsie trwa 24 h. Oblicz przyspieszenie odśrodkowe na równiku Marsa.
A7) Ciało o małej masie spoczywające na wysokości H = RM/33 spadło swobodnie na powierzchnię Marsa. Uzasadnij, że
prędkość z jaką uderzyło o powierzchnię Marsa należy wyznaczyć ze wzoru
GM (17 ⋅ R M ) .
A8) Wyjaśnij dlaczego płaszczyzna orbity Marsa wokół Słońca nie zmienia swojego położenia w przestrzeni.
2
A9) Wyobraź sobie, że znajdujesz się na pokładzie stacji planetarnej zbudowanej przez ziemian
stojącej nieruchomo na powierzchni Marsa i mierzysz siłę FA działającą na sprężynę ze strony ciała
o znanej objętości V i gęstości masy ρ zanurzonego w wodzie o gęstości ρw (patrz rysunek obok).
Podaj wzór na obliczenie wartości FA. Czy warunek pływania ciał w wodzie na marsjańskiej stacji
jest taki sam, jak na powierzchni Ziemi, gdzie ma postać ρw ≥ ρ?
A10) Wyprowadź wzory na liniową prędkość i odległość od środka Marsa jego
stacjonarnego satelity przyjmując za dane: M – masę Marsa, czas T trwania doby
marsjańskiej, stałą grawitacji G.
A11) Wyobraź sobie, że na pokładzie stacji planetarnej zbudowanej przez ziemian na Marsie spoczywają
na powierzchni stołu trzy identyczne jednorodne kulki o masach m, które są
położone na odcinku o długości 2D, przy czym środkową dzieli od
pozostałych odległość D. Jaką pracę wykonają siły oddziaływań grawitacyjnych tych kulek przy przesunięciu jednej ze skrajnych kulek do
nieskończoności?
A12) Mars Reconnaissance Orbiter to amerykańska naukowotelekomunikacyjna sonda kosmiczna (patrz fotografia po prawej stronie),
wystrzelona przez NASA w kierunku Marsa 12.08.2005r, która weszła na orbitę planety 10.03.2006.
Sonda ta okrąża Mars w czasie 114 minut po orbicie kołowej na wysokości 300 km nad powierzchnią
Marsa, którego promień R = 3400 km. Wyznacz na tej podstawie masę Marsa.
--------------------------------------------------------------------------------------
IV. A) Podaj treść fizyczną zasady zachowania pędu dla pojedynczego ciała oraz układu N ciał określając
warunki stosowalności tej zasady.
B) Wyprowadź zasadę zachowania pędu dla układu N ciał oddziaływujących między sobą siłami
spełniającymi III zasadę dynamiki .
C) Pokaż, przyjmując stosowne założenia, że w zderzeniach centralnych dwóch ciał spełniona jest zasada
zachowania pędu.
D) Dwa krążki hokejowe o równych masach 0,1 kg ślizgające się naprzeciw siebie po tafli lodowej zderzyły
się centralnie. Tuż przed zderzeniem wartości ich wektorów prędkości były także równe i wynosiły 5 m/s.
Zakładając, że zderzenie jest idealnie sprężyste oraz że współczynnik tarcia o taflę wynosi 0,03 – wyznacz
odległość d, jaka po zderzeniu dzieli te krążki, gdy każdy z nich zatrzyma się. Ile wynosiłaby odległość
d, gdyby zderzenie było idealnie niesprężyste?
E) W wahadło balistyczne o masie m2 uderzył pocisk o masie m1,
prędkości początkowej v0, przebił je i wyleciał z prędkością v0/3
(patrz rysunek obok). Na jaką wysokośc h wzniosło się wahadło?
F) Pokaż, że w zderzeniach
centralnych idealnie sprężystych dwóch kul o masach
m1 i m2 o prędkościach początkowych v1i i v2i, prędkości
tych kulek po zderzeniu określają wzory podane po lewej stronie
(należy te wzory wyprowadzić).
G) Zdjęcia obok pokazują wynik zderzenia się wystrzelonej ze sprężynowej
wyrzutni kulki o masie m, która po zderzeniu się z wahadłem balistycznym o masie
M grzęźnie w nim i powoduje jego wzniesienie się na wysokość h. Jak wyznaczamy
na podstawie podanych wielkości prędkość kulki oraz stratę energii kinetycznej
kulki?
3
V. A) Opisz sens fizyczny drugiej zasady dynamiki ruchu obrotowego bryły sztywnej wirującej wokół
ustalonej osi obrotu będącej jej osią symetrii. Jakie znasz dwie matematycznie i fizycznie rożne postacie tej
zasady? Opisz sens fizyczny użytych do ich matematycznego zapisu wielkości fizycznych podając ich
jednostki miary. Na czym polega zjawisku precesji bryły sztywnej?
B) Felix Baumgartner, wykonując 14.10.2012 skok ze stratosfery z wysokości 38 969 m, po czasie
40 s osiągnął maksymalną prędkość 1357,6 km/h (1,25 Macha), z którą, niewiele zmieniająca się co do
wartości, spadał jeszcze przez 220 s zanim otworzył się spadochron. Całkowity czas skoku to 543 s.
B1) Oszacuj przybliżoną wartość siły oporu działającą na skoczka po 40 s ale przed 70 s lotu, jeśli masa
układu skoczek + skafander wynosiła 250 kg.
C) W trakcie swobodnego spadku, po około 70 sekundach układ skoczek+skafander został wprawiony
w ruch obrotowy wokół ustalonej, co do kierunku, osi obrotu z rosnącą prędkością kątową.
C1) Wyjaśnij, jaka mogła być przyczyna tego ruchu obrotowego?
Po osiągnięciu maksymalnej, dopuszczalnej względami bezpieczeństwa, prędkości kątowej Ω ruchu
obrotowego włączyły się silniki wytwarzające wypadkowy moment sił M hamujący ruch obrotowy.
Załóżmy, że moment bezwładności układu skoczek + skafander względem osi obrotu wynosił J. Traktując
Ω, M i J jako dane, wyznaczyć:
C2) Wartość czasu t działania silników, po upływie którego ustał ruch obrotowy;
C3) Wartość pracy wykonanej przez silniki podczas hamowania ruchu obrotowego;
C4) Średnią wartość mocy silników spowalniających ruch obrotowy.
D) Dynamika ruchu postępowo obrotowego bryły sztywnej. Na wierzchołu równi pochyłej spoczywają:
walec (Iw = m·r2/2), obręcz (Io = m·r2), kula (Ik = 2m·r2/5), sfera (Is = 2m·r2/3), kula o nierodnym rozkładzie
masy (I = 3m·r2/5). Wszystkie te ciała mają identyczne masy oraz promienie. Która z tych brył staczy
z równi jako ostatnia, jeśli poruszają się bez poślizgu? Swój wybór uzasadnij.
--------------------------------------------------------------------------------------------------------------VI. A) Podaj fizyczny sens zasady zachowania momentu pędu bryły sztywnej określając warunki
stosowalności tej zasady; opisz jednostki miary wielkości fizycznych i znaczenie symboli użytych w zapisie
matematycznym tej zasady.
B) Zawodnik o masie 45 kg wykonujący skok do wody z wieży o wysokości 10 m, w chwili tuż po odbiciu
się od platformy wieży: a) ma prędkość kątową 12 rad/s i moment bezwładności 1,9 kg⋅m2 względem osi
obrotu, wynikający z przyjętej postawy (tułów i kończyny górne przylegają do kończyn dolnych);
b) środek masy ciała skoczka znajduje się na wysokości 1,2 m nad platformą wieży i wartość wektora
prędkości poziomej środka masy zawodnika w tym miejscu toru jest równa 0,8 m/s. Wchodzenie ciała
zawodnika do wody rozpoczyna się w chwili czasu t0, gdy jego środek masy znajduje się w odległości
0,9 m od powierzchni wody a jego sylwetka jest wyprostowana, co zwiększa czterokrotnie jego moment
bezwładności względem poziomej osi obrotu przechodzącej przez środek ciała zawodnika.
B1) Sporządź rysunek toru ruchu skoczka i zaznacz na nim podane odległości.
B2) Wyznacz wartość czasu t0, w którym skoczek spadał swobodnie z najwyższego punktu toru do
momentu wyprostowania ciała i rozpoczęcia wchodzenia palców dłoni zawodnika do wody.
W chwili czasu t0 wyznaczyć:
B3) Prędkość kątową ciała zawodnika.
B4) Prędkość liniową środka masy ciała skoczka.
B5) Całkowitą energię mechaniczną ciała zawodnika.
B6) Wartość całkowitego przyspieszenia palców dłoni zawodnika.
4
d2 x (t )
+ ω02 x ( t ) = 0,
VII. A) Scharakteryzuj kinematykę i dynamikę ruchu drgającego danego równaniem
dt 2
jeśli znana jest wartość parametru ω0. Jaka jest jednostka miary ω0? Podaj postać zależności x(t), wyjaśnij
sens fizyczny użytych symboli, podaj przykłady układów fizycznych, których ruch drgający opisuje
powyższe równanie. Przy jakich warunkach powyższe równanie jest słuszne? Jak warunków początkowych
wyznaczamy amplitudę oraz fazę początkową drgań?
A1) Uzasadnij, że okres drgań opisanych powyższym równaniem wyraża się wzorem T = 2 π ω0 .
A2) Pokaż, że energia kinetyczna ciała o masie m wykonującego drgania opisane powyższym
równaniem jest zachowana.
A3) Uzasadnij stwierdzenie: Jeśli pionowo zwisająca sprężyna wydłuży się ∆x po podwieszeniu do
niej ciała, to okres małych drgań tego ciała na tej sprężynie jest równy okresowi małych drgań
wahadła matematycznego o długości l = ∆x.
B) Wyznaczanie wartości okresów małych drgań.
B1) Do pionowo wiszącej swobodnie sprężyny o współ. sprężystości k1 (jej górny koniec jest zamocowany) podwieszono inną sprężynę o współ. sprężystości k2. Do swobodnego końca dolnej sprężyny
podwieszono ciało o masie M. Wyznacz okres małych drgań podwieszonego ciała w tym układzie.
B2) Cienką jednorodną obręcz o promieniu R zawieszono na poziomym pręcie i wprawiono w małe drganie. Obręcz wykonuje drgania w ten sposób, że jej płaszczyzna jest
prostopadła do pręta. Wyznacz okres tych drgań.
B3) ) Rysunek z lewej strony przedstawia dwie identyczne sprężyny
połączone równolegle, do których podwieszono ciało o masie m. Rysunek
po prawej stronie przedstawia te same sprężyny połączone szeregowo, a
ciało o masie m jest podwieszone do sprężyny niższej. Pokaż, że okres
małych drgań ciała o masie m podwieszonego jak na rysunku z prawej
strony jest dwukrotnie dłuższy od okresu małych drgań tego ciała
podwieszonego na rys. z lewej strony.
B4) Wahadło fizyczne o masie m jest podwieszone w punkcie O (Pivot), co ilustruje rysunek i jego
moment bezwładności względem osi prostopadłej do płaszczyzny rysunku przechodzącej przez
środek masy CM wynosi ICM. Uzasadnij, że okres małych drgań
tego wahadła względem osi prostopadłej do płaszczyzny rysunku i
2
przechodzącej przez punkt O dany jest wzorem T = 2π I CM + md .
mgd
B5) Pokaż, że wartość okresu T
osiąga minimum dla
I CM
.
m
C) Wyjaśnij sens fizyczny zjawiska rezonansu mechanicznego.
d min. =
5
VIII. A) Podaj treść zasady zachowania energii mechanicznej. Określ, przy jakich warunkach można ją
stosować/jest spełniona. Zdefiniuj pojęcia: siły zachowawczej i energii potencjalnej. Podaj treść i przedstaw
wyprowadzenie twierdzenia o pracy i energii kinetycznej. Wyprowadź zasadę zachowania energii
mechanicznej ciała poddanego działaniu siły zachowawczej i wykonującego dowolny ruch w polu tej siły.
C) Dolna powierzchnia budowalnego młota kafara (model-zabawka na zdjęciu obok)
odległa jest o 4,4 m od górnej powierzchni stojącego nieruchomo pionowo i wbijanego
w grunt słupa budowlanego. Środek masy spadającego pionowo w dół młota o masie
200 kg przemieścił się na odległość 4,46 m.
B1) Z jaką średnią siłą działał młot na słup w trakcie zderzenia z powierzchnią słupa?
B2) Jaką wartość prędkości miał środek masy kafara, gdy uderzał w słup?
B3) Samochód, którego wektor prędkości początkowej ma wartość 12 m/s hamuje na
drodze o długości s0. Jeśli ten samochód jadący początkowo z prędkością 58 m/s zacznie
hamować, to jaka będzie jego droga hamowania (hamowanie zachodzi na tej samej
nawierzchni) wyrażona za pomocą wielokrotności s0?
B4) Kulkę o masie m = 0,12 kg rzucono pionowo w dół z wysokości H = 25,4 m
nadając jej prędkość początkową v0 = 3,2 m/s (patrz rysunek po lewej stronie).
Podczas spadku swobodnego działa na kulkę siła oporu ośrodka. Wartość pracy siły
oporu, gdy ciało jest na wysokości 0 ≤ h ≤ H, wynosi mg(h – H)/2. Oblicz prędkość
kulki w chwili, gdy znajduje się na wysokości h = H/3. Ws-ka: ∆Emechaniczna = Praca sił
oporu.
B5) Z wierzchołka komina o wysokości H rzucono N kulek nadając im te same prędkości ale pod
różnymi kątami αi (1≤ i ≤N, αi ≠ αj dla i ≠ j) do poziomu. Uzasadnij stwierdzenie: Jeśli pominąć
opory powietrza, to każda z kulek będąc na wysokości h = H/4 ma taką samą, co do wartości,
prędkość.
C) Rozważmy układ zamknięty jaki tworzą Ziemia i kulka spadająca na powierzchnię Ziemi z małej
wysokości h dużo mniejszej od promienia Ziemi R. Energia kinetyczna układu Ziemia+kulka jest sumą
energii kinetycznych obu ciał (Ziemi i kulki). Jednak w przypadku spadku kulki z niewielkiej wysokości
ℎ ≪ nie uwzględnia się energii kinetycznej Ziemi. Wyjaśnij dlaczego tak
możemy postępować? Ws-ka: Pokaż, że iloraz energii kinetyczne kulki i
energii kinetycznej Ziemi, w opisanym przypadku, wynosi MZiemi/mkulki.
D) Ciało o masie 4 kg jest przemieszczane z początku układu współrzędnych
do punktu C (patrz rysunek po lewej stronie), gdy jedyną siłą działającą na nie
jest siła grawitacji ziemskiej o zwrocie przeciwnym do osi OY. Wyznacz
prace siły grawitacji na drogach: a) OA C, b) OBC, c) OC (po przekątnej
kwadratu OBCA).
IX. A) Podaj definicję fali sprężystej. Jakie konieczne warunki powinny być spełnione, aby możliwe było
obserwowanie fal sprężystych? Jakie rodzaje prędkości są związane z ruchem falowym? Jak prędkość
propagowania się fali zależy od właściwości mechanicznych ośrodka?
B) W długiej strunie, naciągniętej siłą 200 N propaguje się fala poprzeczna postaci
y ( x , t ) = 10 −4 sin ( 2πt − 2 ⋅ 10 −2 πx ) .
B1) Opisz sens fizyczny użytych w powyższej formule wielkości/wartości.
B2) Wyznacz okres i prędkość fazową tej fali.
6
B3) Jak zależą od czasu wychylenia z położeń równowagi elementów struny znajdujących się w odległości
100 m od źródła fali?
B4) Jaka jest gęstość liniowa masy tej struny?
B5) Oblicz maksymalną wartość energii, jaką może pobrać od tej struny odbiornik umieszczony
w odległości 100 m od źródła.
C) Zmierzono zależność okresu T tonu podstawowego dźwięku wytwarzanego przez naciągniętą i zamocowaną dwustronnie strunę, od jej długości L.
Wyniki pomiarów ilustruje sąsiedni wykres.
Oszacuj w m/s prędkość c fali akustycznej rozchodzącej się w tej strunie. Jaki powinien być naciąg
struny w każdym z pomiarów, aby oszacowana
wartość prędkości c była wiarygodna?
D) Wzdłuż naciągniętej struny rozchodzi się fala
kosinusoidalna o okresie T = 0.1 s z prędkością c =
40 m/s. Po upływie czasu t1= 10 s od rozpoczęcia
drgań źródła w odległości (62/3) m od niego wychylenie z położenia równowagi elementów ośrodka było
równe 2 cm. Określić w tym samym momencie czasu wychylenie elementów ośrodka znajdujących się
w odległości (73/3) m od źródła.
E) Udowodnij, że fala podłużna u ( x , t ) = A sin ( ωt − kx ) biegnąca w jednorodnym pręcie o gęstości masy
ρ wnosi do fragmentu tego pręta o masie ∆m i rozmiarach liniowych dużo mniejszych od długości tej fali,
energię równą ∆m⋅v2/2, gdzie v jest maksymalną prędkością drgań fragmentu preta o masie ∆m wokół
położenia równowagi.
---------------------------------------------------------------------------X. A) Scharakteryzuj sens fizyczny prawa Gaussa dla pola elektrostatycznego i magentostatycznego.
B) Wyprowadzić prawo Coulomba z prawa Gaussa. Wyprowadzenie opatrzyć stosownymi komentarzami
słownymi , których brak będzie dyskwalifikował wyprowadzenie.
C) Pokaż, że wartość natężenia E pola elektrycznego między okładkami powietrznego kondensatora
płaskiego o bardzo dużej powierzchni S, na okładkach którego zgromadzono ładunek Q na jednej i (–Q)
na drugiej, wynosi E = Q ( ε0 S ) .
D) W narożach równobocznego trójkąta o boku a znajdują się dodatnie ładunki Q, a w jego środku ładunek
ujemny (–q). Oblicz najmniejszą pracę jaką wykona siła zewnętrzna przy przemieszczeniu ładunków –
q na bardzo dużą odległość od pozostałych (można przyjąć, że ładunek –q przemieszczono do
nieskończoności).
E) Proton o wartości prędkości 2,0ˑ106 m/s porusza się (w przybliżeniu) po orbicie kołowej (w próżni) tuż
nad naładowaną metalową sferą o promieniu 3 cm. Jaki jest ładunek Q na sferze?
F) Wyprowadź wzór na pojemność płaskiego, próżniowego kondensatora płaskiego. Dlaczego pojemność
takiego kondensatora wzrośnie, gdy między jego okładki wprowadzony zostanie dielektryk>
G) W polu elektrostatycznym ładunku punktowego Q umieszczonego w próżni jest zgromadzona w pełni
określony zapas energii elektrostatycznej, której gęstość wyraża się wzorem ρ = ε0 E 2 2. Oblicz całkowitą
energię elektrostatyczną W pola ładunku punktowego zgromadzoną pomiędzy dwoma sferami o promieniach
R1 < R2 i wspólnym środku, w którym znajduje się ładunek Q. Ws-ka: Wkład do dW pochodzący od
objętości wypełniającej obszar pomiędzy koncentrycznymi sferami o promieniach r oraz r + dr wynosi
dW = 4πr 2ρdr.
7
H) Dodatni ładunek +q jest przemieszczane z początku układu współrzędnych
do punktu C (patrz rysunek po lewej stronie), gdy jedyną siłą działającą na
niego jest siła pochodząca od pola elektrostatycznego o zwrocie zgodnym ze
zwrotem osi OY. Wyznacz prace siły elektrostatycznej na drogach: a) OA C,
b) OBC, c) OC (po przekątnej kwadratu OBCA).
I) Wyprowadź wzór określający pojemność elektryczną baterii złożonej z N
kondensatorów połączonych równolegle.
XI. A) Podaj definicję wektora gęstości prądu elektrycznego. Wyznacz prędkość unoszenia elektronów
o ładunku 1,6⋅10-19 C w metalowym przewodniku, w którym płynie prąd stały o natężeniu 10 A, pole
przekroju poprzecznego przewodnika jest równe 6,25⋅10-6 m2, a koncentracja elektronów wynosi
1029 m-3.
B) Opisz sens fizyczny całkowego i różniczkowego prawa Ohma.
C) Opisz reguły Kirchhoffa przytaczając reguły znaków. Różnica potencjałów VAB między dwoma punktami
B
A i B obwodu elektrycznego wyraża się wzorem VAB = − ∫ E ⋅ dr , gdzie E – wektor natężenia pola, a dr –
A
element obwodu, którego zwrot określa przyjęty kierunek obchodzenia danego oczka.
B) Oblicz natężenia i kierunki płynących prądów w elementach obwodu przedstawionego powyżej. Oblicz
wartości potencjałów w punktach obwodu od d do b, jeśli w punkcie c potencjał jest równy zeru.
C) Wyznacz moc energii wydzielanej na opornikach w układzie pokazanym powyżej.
D) Wyprowadź wzór określający opór zastępczy układu złożonego z N oporników połączonych równolegle.
---------------------------------------------------------------------------------------------XII. A) Opisz reguły Kirchhoffa przytaczając reguły znaków. Różnica potencjałów VAB między dwoma punktami
B
∫
A i B obwodu elektrycznego wyraża się wzorem VAB = − E ⋅ dr , gdzie E – wektor natężenia pola, a dr –
A
element obwodu, którego zwrot określa przyjęty kierunek obchodzenia danego oczka.
B) Oblicz natężenia i kierunki płynących prądów w elementach obwodu przedstawionego powyżej. Oblicz wartości
potencjałów w punktach obwodu od d do b, jeśli w punkcie c potencjał jest równy zeru. Ws-ka: patrz dodatek.
8
C) Opisz prawa Ampere’a i Biota-Savarta podając sens i znaczenie fizyczne użytych symboli w zapisach
matematycznych tych praw oraz jednostki miar wielkości fizycznych występujących w przytaczanych wzorach.
D) W przewodniku kołowym o promieniu R umieszczonym w próżni płynie prąd o natężeniu I. Korzystając z prawa
Biota-Savarta, pokaż, że wektor B indukcji pola magnetycznego w środku koła jest prostopadły do płaszczyzny koła a
jego wartość wynosi B = µ0 I . .
2R
E) W czterech bardzo długich, równoległych przewodnikach przechodzących przez wierzchołki kwadratu o boku a,
płyną w tych samych kierunkach jednakowe prądy o natężeniu I. Oblicz natężenie pola magnetycznego w
geometrycznym środku kwadratu i uzasadnij wartość otrzymanego wyniku. .
G) Silnik magnetohydrodynamiczny (MHD) wykorzystuje do napędu oddziaływanie pola magnetycznego z płynem
przewodzącym prąd elektryczny, np. z elektrolitem soli kuchennej. Taki silnik
(uproszczony schemat przedstawia rys. obok) jest zbudowany z dwóch silnych
sztabkowych magnesów, dwóch miedzianych płytek połączonych do źródła prądu.
Po zanurzeniu takiego silnika w roztworze soli kuchennej, pole magnetyczne
działające na jony Na(+) oraz Cl(–) powoduje odchylenie ich torów, co wywołuje ruch
wody wypełniającej wnętrze silnika, a w konsekwencji wystąpienie siły reakcji, tj.
siły napędzającej ruch silnika względem wody. Opisz w jakim kierunku/kierunkach
i jakie zwroty mają siły pochodzące od pola magnetycznego i działające na jony. Oblicz wartość siły działającej na
wodę wypełniającą silnik, jeśli a = 3 cm, b = 1,5 cm i c = 1 cm, wartość indukcji pola magnetycznego B = 0,4 T a natężenie prądu płynącego między miedzianymi płytkami wynosi 1 A.
H) Do dwóch ogniw o oporach wewnętrznych Rw podanych na rysunku obok dołączono oporniki regulowane.
Zmieniano opór elektrycznych oporników Rzew i mierzono jednocześnie
natężenie, napięcie oraz wyznaczano moc użyteczną Pużyt. wydzielanej na
nich energii elektrycznej. Sporządzono wykresy zależności Pużyt.(Rzew);
patrz rys. obok. Na podstawie pomiarów postawiono tezę, że maksymalna
moc użyteczna jest obserwowana dla oporu zewnętrznego równego
oporowi wewnętrznemu ogniw. Czy postawiona teza jest prawdziwa.
Napisz odpowiedź i uzasadnij ją.
---------------------------------------------------------------------------------------------------------------------------------XIII.
A) Opisz sens fizyczny praw Keplera i dwa spośród nich (nie dotyczące torów planet) udowodnij. Wyjaśnij,
dlaczego wartość prędkości Marsa na orbicie okołosłonecznej w rzeczywistości nie jest stała.
B) Zakładając, że orbita Marsa jest okręgiem o promieniu
227, 9 ⋅ 109 m, znając masę Słońca 2 ⋅ 1030 kg,
G = 6,7 ⋅ 10−11 m3/kg/s2 wyznacz:
B1) Czas trwania „jednego roku marsjańskiego”, tj. jednego obiegu Słońca przez tę planetę.
B2) Wartość wektora natężenia pola grawitacyjnego na powierzchni Marsa, którego masa jest równa 6, 4 ⋅ 10 23 kg.
B3) Całkowitą energię mechaniczną Marsa w polu grawitacyjnym Słońca.
B4) Pierwszą i drugą prędkość kosmiczną dla tej planety, jeśli jej średnica wynosi 6780 km.
B5) Czas trwania jednej doby marsjańskiej wyrażony w godzinach i minutach, jeśli prędkość punktów na równiku
wynosi 241 m/s.
B6) Po upływie czasu t położenia Ziemi i Marsa na orbicie okołosłonecznej zajmują cyklicznie w przestrzeni
położenia leżące na prostej przechodzącej przez planety i Słońce. Oblicz wartość t w latach ziemskich.
B7) Wyznacz odległość d od środka Marsa i prędkość liniową V umieszczonego na orbicie wokół Marsa satelity
geostacjonarnego.
9
B8) Poszukiwacze planet pozasłonecznych twierdzą, że na chwilę obecną odkryli ponad 1400 takich obiektów krążących wokół
gwiazdy (lub gwiazd) innej niż Słońce. Jedna z takich planet kulistych ma promień R i przyspieszenie swobodnego spadku na
biegunie tej planety jest o ∆g większe od przyspieszenia swobodnego spadku na jej równiku. Uzasadnij, że okres obrotu tej
planety wokół własnej osi wyraża się wzorem
T = 2π
R
.
∆g
------------------------------------------------------------------------------------------------------------------------------------------XIV. A) Opisz sens fizyczny prawa indukcji elektromagnetycznej Faraday’a oraz reguły Lenza. Wyjaśnij sens
fizyczny tego prawa w kontekście zasady zachowania energii.
B) Rysunek A przedstawia mały fragment długiego przewodnika z prądem o natężeniu I, którego kierunek
przepływu pokazuje strzałka. W pobliżu tego przewodnika znajduje się prostokątna miedziana ramka. Opisz
kierunki przepływu prądu, gdy ramka będzie: a) przysuwana do przewodnika, jak pokazuje wektor R; b) odsuwana
od przewodnika, jak pokazuje wektor P; c) przysuwana równolegle do przewodnika i płynącego w nim prądu, jak
pokazuje wektor Z.
R
A
P
P
b
I
T
Rys. B
Rys. A
Miedziany drut P jest przesuwany po metalowych sztywnych prętach miedzianych, jak na rysunku B, w polu magnetycznym z
przyspieszeniem a w kierunku wskazanym strzałką. Początkowe położenie drutu P, dla t = 0 sek., pokrywało się z linią
przerywaną. Zakładając, że w chwili początkowej prędkość poprzeczki P była równa zeru, dla chwili czasu t > 0:
B1) Oblicz wartość natężenia prądu I(t), przyjmując, że opór R(t) układu jest dany.
B2) Czy kierunek przepływu prądu I(t) w układzie z rysunku jest zgodny czy niezgodny z ruchem wskazówek
zegara?
B3) Wyznacz moc siły zewnętrznej, przyłożonej do P.
C) Opisz krótko konwersje energii, z którymi mamy do czynienia w punktach A) i B).
D)
Co zmieni się w obrazie fizycznym zadania z pkt. B), gdy metalowa poprzeczka P będzie przesuwana po
szklanych rurkach?
-------------------------------------------------------------------------------------------
d2 x (t ) E
+ x ( t ) = 0, gdzie E jest natężeniem pola
XIV. Równanie ruchu drgań wahadła matematycznego ma postać
dt 2
L
grawitacyjnego w miejscu, gdzie wahadło wykonuje ruch drgający.
A1) Dla jakich wartości stałego parametru z funkcja x ( t ) = A ⋅ sin ( z ⋅ t + α ) jest rozwiązaniem powyższego równania
ruchu?
A2) Jak okres T drgań wahadła matematycznego z A1) zależy od z, a jak od E i długości L wahadła?
A3) Masa Ziemi i jej średni promień wynoszą, odpowiednio, 6·1024 kg i 6371 km. Te same dane dla Marsa są równe
6, 4 ⋅ 10 23 kg i 3389 km. Wyznacz stosunek okresów TZiemi TMarsa drgań wahadeł matematycznych wahających się na
−11
powierzchni tych planet; G = 6,7 ⋅ 10 m3/kg/s2.
10
A4) Załóżmy, że dwa identyczne tłoki rozmieszczone są na powierzchni Ziemi i Marsa i poruszają się pionowo
ruchem harmonicznym. Na poziomych powierzchniach tych tłoków znajdują się klocki o masach m. Niechaj
okresy drgań obu tłoków wynoszą 2 sek. Oblicz przy jakich minimalnych wartościach amplitud drgań tłoków na
Ziemi i na Marsie klocki i tłoki rozłączą się?
A5) Na rys. obok przedstawiony jest dźwig burzący, którego kula o masie 1200 kg
jest podwieszona na linie o długości 9 m. Potraktuj cały układ jako wahadło
matematyczne i wyznacz okres małych drgań kuli.
A6) Początkowy kąt wychylenia kuli od pionu wynosi 60o (nie jest pokazany na
rysunku). Kula uderza w betonową ścianę burzonego muru, gdy lina tworzy kąt 30o
z pionem (moment uderzenia pokazany na rysunku). Zderzenie trwa 0,002 s,
podczas którego praktycznie cała energia kuli jest przekazywana burzonej ścianie
muru, przy czym kula przemieszcza się w murze na odległość 1 cm. Wyznacz
średnią wartość siły z jaką kula podczas takiego uderzenia działa na mur.
A7) Na rys. obok przedstawiony jest pręt o podanych wymiarach, masie M,
który może wykonywać małe drgania wokół punktu zawieszenia O. Wyznacz
okres T małych drgań tego pręta jako funkcję x i L. tj. T(x,L). Dla jakich
wartości x okres T jest najmniejszy?
A8) W latach 80-ych XX wieku nawierzchnię tzw. autostrady A-4 stanowiły
betonowe płyty każda o długości L. Przez kilkadziesiąt lat użytkowania, po
1945 r., nawierzchnia uległa znacznym deformacjom w wyniku pionowych
przesunięć płyt oraz ich zużycia w pobliżu styków. Niektórzy złośliwie nazywali ją "najdłuższymi schodami nowoczesnej Europy". Samochód o masie M wiozący pasażerów o łącznej masie m,
jadący w latach 80-ych XX w. po starej autostradzie A-4, wyposażony w resory o współczynniku sprężystości K,
przy określonej prędkości ruchu V0 wykonywał w kierunku pionowym drgania o znacznie większej amplitudzie niż
przy prędkościach ruchu V ≠ V0. Oblicz wartość V0 i wyjaśnij opisane zjawisko. Obliczenia wykonaj dla: K =
65 000 N/m, M = 800 kg, M = 230 kg, L = 7 m. Wynik podaj w km/h.
A9) Poszukiwacze planet pozasłonecznych twierdzą, że na chwilę obecną odkryli ponad 1400 takich obiektów
krążących wokół gwiazdy (lub gwiazd) innej niż Słońce. Jedna z takich planet kulistych ma masę trzykrotnie
mniejszą od masy Ziemi a jej promień stanowi 75% promienia Ziemi. Dla jakiej długości L okres drgań wahadła
matematycznego umieszczonego na powierzchni tej planety byłby równy 1s?
--------------------------------------------------------------------------------------------------------XV.
A) Podaj definicję fal sprężystych. Jakie konieczne warunki powinny być spełnione, aby możliwe było
obserwowanie fal sprężystych? Jakie rodzaje prędkości są związane z falami sprężystymi? Opisz zjawisko
interferencji fal sprężystych.
B) W długiej strunie, naciągniętej siłą 200 N propaguje się fala poprzeczna y ( x , t ) = 10 −4 sin ( 2 πt − 2 ⋅ 10 −2 πx ) – wzór
podano w SI.
B1) Opisz sens fizyczny użytych w powyższej formule wielkości/wartości podając ich jednostki miary. .
B2) Wyznacz okres i prędkość fazową tej fali.
B3) Udowodnij, że średnia prędkość elementów (cząsteczek) ośrodka sprężystego rozpatrywanej fali spełnia równość
V =
1 dy ( x , t )
= 0.
T
dt
B4) Jak zależą od czasu prędkości elementów struny znajdujące się w odległości 100 m od źródła fali?
B5) Jaka jest gęstość liniowa masy tej struny?
11
B6) Przyjmując, że średnie prędkości powierzchniowych fal sejsmicznych podłużnych i poprzecznych wynoszą,
odpowiednio 3050 m/s i 1760 m/s, obliczyć odległość epicentrum trzęsienia od stacji sejsmograficznej, jeśli
zarejestrowana różnica czasu w nadejściu fal do stacji wyniosła 197,8 s. Wynik końcowy podaj z dokładnością do
jednego kilometra.
B7) Podczas mgły syrena stojącego nieruchomo statku wysyła sygnały dźwiękowe o częstotliwości 3 kHz. Rybak na
kutrze płynącym w stronę statku odbiera dźwięki syreny o częstotliwości 3,05 kHz. Przyjmując, że prędkość dźwięku
we mgle wynosi 330 m/s oblicz wartość prędkości kutra.
-----------------------------------------------------------------------------------------------------------------------------3
3
XVI. W bardzo długiej tubie jednostronnie otwartej umieszczonej w wodzie o gęstości 10 kg/m , rozchodzi się dźwięk
y ( x, t ) = 10−6 sin ( 62580πt − 42πx ) .
A1) Wyznacz częstotliwość, długość, prędkość fazową tej fali oraz współczynnik ściśliwości wody.
A2) Oblicz średnią intensywność (natężenie) < J > tej fali.
A3) Oblicz średnią gęstość energii < ρ > tej fali.
A4) Oblicz średnią wartość siły wywieranej przez tę falę padającą prostopadle na płaska powierzchnię urządzenia
zamocowanego wewnątrz tuby o polu przekroju 1,44·10-4 m2.
*A5) Oblicz częstości dźwięków (tonów własnych), których źródłem może być tuba opisana w A, jeśli jej długość jest
skończona i wynosi 2,85 m.
-----------------------------------------------------------------------------------------------------------------------------XVI. A) Podaj treść zasady zachowania energii mechanicznej. Określ, przy jakich warunkach można ją stosować/jest spełniona.
Zdefiniuj pojęcia: siły zachowawczej i energii potencjalnej. Podaj treść i przedstaw wyprowadzenie twierdzenia o pracy i energii
kinetycznej. Wyprowadź zasadę zachowania energii mechanicznej ciała poddanego działaniu siły zachowawczej.
D) Dolna powierzchnia budowlanego młota kafara (model-zabawka na zdjęciu obok) odległa jest o 4,4 m
od górnej powierzchni stojącego nieruchomo pionowo i wbijanego w grunt słupa budowlanego. Środek
masy spadającego pionowo w dół młota o masie 200 kg przemieścił się na odległość 4,46 m.
B1) Z jaką średnią siłą działał młot na słup w trakcie zderzenia z powierzchnią słupa?
B2) Jaką wartość prędkości miał środek masy kafara, gdy uderzał w słup?
B3) Samochód, którego wektor prędkości początkowej ma wartość 12 m/s hamuje na drodze o długości
s0. Jeśli ten samochód jadący z prędkością 58 m/s zacznie hamować, to jaka będzie jego droga hamowania
(hamowanie zachodzi na tej samej nawierzchni) wyrażona za pomocą wielokrotności s0?
B4) Kulkę o masie m = 0,12 kg rzucono pionowo w dół z wysokości H = 25,4 m nadając jej prędkość początkową v0 = 3,2 m/s (patrz rysunek po prawej stronie). Podczas spadku swobodnego działa na kulkę siła
oporu ośrodka. Wartość pracy siły oporu, gdy ciało jest na wysokości 0 ≤ h ≤ H, wynosi mg(h – H)/2.
Oblicz prędkość kulki w chwili, gdy znajduje się na wysokości h = H/3. Ws-ka: ∆Emechaniczna = Praca sił
oporu.
B5) Z wierzchołka komina o wysokości H rzucono N kulek nadając im te same prędkości ale pod różnymi
kątami αi (1≤ i ≤N, αi ≠ αj dla i ≠ j) do poziomu. Uzasadnij stwierdzenie: Jeśli pominąć opory powietrza, to
każda z kulek będąc na wysokości h = H/4 ma taką samą, co do wartości, prędkość.
B6) Nieruchomo jądro neodymu ulega rozpadowi
następującą postać:
144
60
α
i powstaje jądro ceru, a schemat rozpadu ma
4
Nd → 140
58 Ce + 2 He + E ,
gdzie E jest energią wydzieloną podczas rozpadu, a masy jąder biorących udział w rozpadzie wynoszą:
mNd = 143,9099 ⋅ u, mCe = 139,9053 ⋅ u, mHe = 4,0026 ⋅ u,
u = 1,6605 ⋅ 10−27 kg = 931,4940
12
MeV
.
c2
B6.1) Uzasadnij, że podczas opisanego rozpadu wyzwalana jest energia E = 1,863 MeV = 2.981·10
eV ≅ 1,6·10
-19
-13
J; przyjąć, że
1
J.
B6.2) Zakładając, że elementy rozpadu mają prędkości znacznie mniejsze od prędkości światła (rozpad nierelatywistyczny),
uzasadnij, że zarówno jądro ceru jak i cząstka α mają po rozpadzie wartości pędów dane wzorem:
pCe = pHe =
2 ⋅ E ⋅ mHe ⋅ mCe
.
mHe + mCe
-------------------------------------------------------------------------------------------------------------------------------------XVII.
A) Opisz wyniki podstawowych doświadczeń dotyczących zjawiska fotoelektrycznego i zjawiska Comptona nie
wykorzystując przy tym żadnych wzorów matematycznych.
B) Wyjaśnij fizyczne znaczenie symboli użytych we wzorze Comptona ∆λ = λ − λ0 =
h
(1 − cos Θ) . Z jakich
m0c
praw/zasad korzysta się przy wyprowadzaniu tego wzoru?
C) Progowa długość fali dla potasu wynosi 558 nm. Oblicz napięcie hamujące dla potasu oświetlonego falą
elektromagnetyczną o długości 400 nm.
D) Promień atomu potasu wynosi 10-10 m. Niechaj atom K będzie oświetlany falą z zad. C) o wartości natężeniu
2·10-2 W/m2. Ile czasu t upłynie zanim atom potasu pochłaniający całkowicie padające promieniowanie
zaabsorbuje energię równa pracy wyjścia. Wynik podać w minutach.
E) Załóżmy, że jeden na miliard fotonów promieniowania z zad C) padających na powierzchnię 1m2 potasu
powoduje wybicie fotoelektronu. Jaką wartość ma w tych warunkach wektor gęstości prądu?
F) Podaj i krótko scharakteryzuj co najmniej 3 zastosowania fotoefektu.
-------------------------------------------------------------------------------------------------------------------------XVIII.
A) Napięcie 100 kV jest przyłożone między katodą i wolframową anodą lampy rentgenowskiej. Jaka jest krótkofalowa
granica promieniowania ciągłego tej lampy? Wyjaśnij sens fizyczny tego ograniczenia i podaj przedziały długości i
częstotliwości emitowanego przez tę lampę promieniowania X.
B) Metaliczny α-polon ma gęstość 9196 kg/m3, masę molową 0,21 kg i krystalizuje w strukturze sieci kubicznej
prostej, co oznacza, że atomy polonu są rozmieszczone w objętości kryształu polonu w wierzchołkach komórek
elementarnych, którymi są identyczne sześciany o boku d. Oszacować wartość d zakładając, że na jeden atom
polonu przypada objętość d3.
C) Promieniowanie charakterystyczne Kα wolframowej anody lampy rentgenowskiej ma długość fali równą 2,1·10-11
m. Jakie najmniejsze napięcie przyłożone do takiej lampy pozwala, na tle widma ciągłego takiej lampy,
zaobserwować linię Kα?
D) Wyznaczyć kąt, pod jakim musi być zorientowany kryształ α-polonu (patrz punkt B)) względem padającego nań
promieniowania Kα (patrz zad. C)), aby można było zaobserwować odbicie Bragga pierwszego rzędu?
13
XIX.
A) Opisz reguły Kirchhoffa przytaczając reguły znaków. Różnica potencjałów VAB między dwoma punktami A i B
B
∫
obwodu elektrycznego wyraża się wzorem VAB = − E ⋅ dr , gdzie E – wektor natężenia pola, a dr – element
A
obwodu, którego zwrot określa przyjęty kierunek obchodzenia danego oczka.
B) Oblicz natężenia i kierunki płynących prądów w elementach obwodu przedstawionego powyżej. Oblicz wartości
potencjałów w punktach obwodu od d do b, jeśli w punkcie c potencjał jest równy zeru. Ws-ka: Patrz dodatek.
C) Opisz prawa Ampere’a i Biota-Savarta podając sens i znaczenie fizyczne użytych symboli w zapisach
matematycznych tych praw oraz jednostki miar wielkości fizycznych występujących w przytoczonych wzorach.
D) W przewodniku kołowym o promieniu R umieszczonym w próżni płynie prąd o natężeniu I. Korzystając
z prawa Biota-Savarta, pokaż, że wektor B indukcji pola magnetycznego w środku koła jest prostopadły do
płaszczyzny koła a jego wartość wynosi B =
µ0 I
.
2R
E) W czterech bardzo długich, równoległych przewodnikach przechodzących przez wierzchołki kwadratu o boku a,
płyną w tych samych kierunkach jednakowe prądy o natężeniu I. Oblicz natężenia pola magnetycznego w
geometrycznym środku kwadratu i w środku wybranego boku kwadratu uzasadniając wartość otrzymanego
wyniku.
---------------------------------------------------------------------------------------------------------------------XX. A) Wzbudzony atom wodoru poruszający się z prędkością (0,9995c; 0,0; 0,0) względem spoczywającego układu
odniesienia, emituje w kierunku przeciwnym do kierunku swego ruchu foton o częstości 1016 Hz. Wyznacz wektor
prędkości wyemitowanego fotonu względem układu spoczywającego? Uzasadnij otrzymany wynik.
B) Gwiazda oddalająca się od spoczywającego układu odniesienia K z prędkością (V; 0,0; 0,0) emituje światło
fioletowe o długości 380 nm, które w układzie K odbierane jest jako światło czerwone o długości 710 nm.
Wyznacz i uzasadnij otrzymaną wartość V.
C) Z działa elektronowego o prędkości (0,9c; 0,0; 0,0) poruszającego się względem spoczywającego inercjalnego
układu odniesienia, wyemitowany został elektron o prędkości (−0,7c; 0,0; 0,0). Wyznacz i uzasadnij wartość
prędkości tego elektronu w układzie poruszającym się z prędkością (0,7c; 0,0; 0,0) względem spoczywającego
układu odniesienia. Ws-ka: Znajdź prędkość wyemitowanego elektronu z działa
inercjalnego układu odniesienia.
14
względem spoczywającego
D) Opisz sens fizyczny transformacji Galileusza, Lorentza i użytych symboli w zapisie matematycznym. W układzie
odniesienia poruszającym się z prędkością (0,02c; 0,0; 0,0) względem spoczywające układu odniesienia, w punkcie
o współrzędnych przestrzennych (−3·102; 0,0; 0,0) m w chwili czasu 10-3 s zapalona została latarka. Wyznacz i
uzasadnij współrzędne przestrzenne i czasowe tego zdarzenia w spoczywającym układzie odniesienia za pomocą
transformacji Galileusza i Lorentza. Oblicz także wartości błędów względnych: δ x =
xG − xL
,
xG
δt =
tG − tL
,
tG
gdzie xG , tG i x L , t L to współrzędne obliczone przy zastosowaniu, odpowiednio, transformacji Galileusza i
Lorentza.
E) W układzie poruszającym się z prędkością (0,2c; 0,0; 0,0) względem spoczywającego układu odniesienia K, w
płaszczyźnie O’X’Y’ spoczywa pręt o masie 0,12 kg, długości własnej 0.6 m tworząc z osią OY’ kąt 60o. Wyznacz
długość tego pręta oraz jego relatywistyczną energię kinetyczną w K.
-----------------------------------------------------------------------------------------------------------------------XXI.
A) Stan kwantowy elektronu znajdującego się w nieskończenie głębokiej studni potencjalnej jest opisany
1
 πnx 
sin 
 , n = 1,2,3,... . Pokaż, że
L
 L 
energia En n-tego stanu kwantowego elektronu w takiej studni jest proporcjonalna do n2. Ws-ka: Energia n-tego stanu spełnia równanie
2
d 2ϕ n ( x )
Schrödingera − ℏ
= En ϕn ( x ) .
2me dx 2
funkcją
ϕn ( x ) =
falową
B) Wyznacz wartość prawdopodobieństwa znalezienia elektronu na przedziale L w przedziale < x; x + dx >,
gdzie x = 3L , dx = 0,009 L.
4
C) Niechaj elektron znajduje się w studni potencjalnej, o której mowa w punkcie A), przy czym L = 1 m. Oblicz
różnicę
poziomów
energetycznych
∆E1,2 = E2 − E1 ,
przyjmując
wartości:
ℏ = 10−34 J ⋅ s, m 2 = 10−31 kg, e = 1,6 ⋅ 10 −19C. Tak policzona różnica odległość jest co do rzędu wielkości
równa różnicy poziomów energetycznych elektronów w metalach, co jest fizyczną przyczyną bardzo dobrego
przewodnictwa elektrycznego metali.
D) Powtórz obliczenia z punktu C) dla L = 10-10 m. Jakie stad wynikają wnioski?
E) Korzystając z wyników otrzymanych w części A) oraz posługując się wzorem En =
pn2
, gdzie pn – pęd
2me
elektronu w n-tym stanie kwantowym, pokaż, że długość λn fali de Broglie’a stowarzyszona z elektronem w
n-tym stanie kwantowym spełnia równość n
λn
= L, n = 1, 2,3,... .
2
15
XXII.
A) Narysuj i opisz schemat budowy oraz wyjaśnij fizyczne podstawy działania cyklotronu. .
B) Pokaż, że częstotliwość rezonansowa f cząstki o masie spoczynkowej m0, ładunku Q przyspieszanej
w cyklotronie, w którym indukcja pola magnetycznego wynosi B dana jest wzorem f =
Q⋅B
.
2πm0
.
C) Pokaż, że częstotliwość rezonansowa f cząstki o masie m, ładunku Q przyspieszanej w cyklotronie do
prędkości relatywistycznych, w którym indukcja pola magnetycznego wynosi B dana jest wzorem
f relatywistyczna = f
m0
.
kinetyczna
Erelatywistyczna
m0 +
c2
D) Niechaj napięcie przyspieszające w cyklotronie wynosi 1 kV. Niech cząsteczką przyspieszaną będzie proton o
masie spoczynkowej 1,7·10-27 kg, ładunku e = 1,6 ⋅ 10−19C. Ile co najmniej razy proton winien być
przyspieszany polem elektrycznym, aby jego prędkość była nie mniejsza od 1% prędkości światła?
Obliczenia przeprowadzić korzystając z formuł klasycznych (nierelatywistycznych).
E) Wyjaśnij fizyczne podstawy klasycznego zjawiska Halla. Podaj przykłady zastosowań tego zjawiska.
F) Trudne. Cienka folia ze złota o grubości
.
D, długości L i szerokości W jest umieszczona w polu
magnetycznym o indukcji B, co ilustruje poniższy rysunek. Dana jest koncentracja n elektronów w folii,
której wartość wynosi n = 6·1028 m-3. Przez folię wzdłuż kierunku równoległego do L przepływa prąd o natężeniu I, ponieważ do folii jest przyłożone zewnętrzne pole elektryczne (niezaznaczone na rysunku), którego
wektor natężenia E jest równoległy do L. Niechaj Vd – oznacza prędkość dryfu elektronów na kierunek
zewnętrznego pola elektrycznego E.
Pokaż, że w warunkach równowagi:
a) wartość natężenia pola elektrycznego Halla na kierunek równoległy do boku W wynosi E H = Vd ⋅ B,
b) wartość napięcia Halla jest równa VH =
I ⋅B
; wyznacz tę wartość dla następujących wartości
D ⋅n ⋅e
A, B = 0,5 T, D =100 µm;
( I ⋅ B) .
2
( D ⋅ n ⋅ e) ⋅ R
2
c) moc wydzielanej energii cieplnej w oporniku R wyraża się wzorem
16
I = 30
XXIII.
A) Opisz prawo indukcji elektromagnetycznej, wyjaśnij sens fizyczny reguły Lenza, podaj metodę wyznaczania
kierunku przepływu indukowanego prądu elektrycznego w zamkniętym obwodzie elektrycznym
umieszczonym w zmiennym polu magnetycznym.
B) Zamknięty obwód elektryczny tworzy kwadratowa ramka o boku a, oporze R umieszczona w płaszczyźnie
poziomej OXY. W obwód ten jest włączona bateria o sile elektromotorycznej
ε i oporze wewnętrznym r.
Prąd płynie w ramce, patrząc na nią z góry, zgodnie z ruchem wskazówek zegara. Płaszczyzna ramki jest
prostopadła do linii stałego pola magnetycznego o indukcji B = (0,0; 0,0; B). Oblicz: a) energię potencjalną
ramki w polu magnetycznym, czy jest stan stabilnej czy chwiejnej równowagi mechanicznej; b) wypadkową
siłę przyłożoną do ramki; c) wektor momentu sił przyłożonych do ramki. Siłę grawitacji zaniedbać. .
C) Załóżmy, że pole magnetyczne, o którym mowa w poprzednim punkcie zależy od czasu t jak B = [0,0; 0,0;
Bo(1 + α·t)], gdzie α > 0 – stała. Wyznacz w tych warunkach wartość natężenia prądu płynącego w ramce.
.
D) Jak zmienią się wyniki z pkt. C), gdy α < 0? Czy wyniki punktu C) i D) zależą od wartości parametru α?
E) Podaj i krótko scharakteryzuj co najmniej 3 zastosowania zjawiska indukcji elektromagnetycznej.
F) W polu magnetostatycznym wytwarzanym przez prostoliniowy bardzo długi przewodnik umieszczony w
próżni, przez który płynie prąd o natężeniu I jest zgromadzona energia tego pola, której gęstość wyraża się
wzorem ρ =
1
µ0 H 2 . Oblicz energię pola magnetycznego wytwarzanego przez prostoliniowy bardzo długi
2
przewodnik, przez który płynie prąd o natężeniu I, zgromadzoną pomiędzy dwoma koncentrycznymi
cylindrami o długości (wysokości) L i promieniach R1 < R2 otaczającymi przewodnik. Ws-ka: Wkład do dW
pochodzący od objętości wypełniającej obszar pomiędzy koncentrycznymi cylindrami o promieniach r oraz r
+ dr wynosi dW = 2πrLρdr.
XXIV. Przedstaw postulaty szczególnej teorii względności.
W systemach globalnego pozycjonowania (GPS) zegary na powierzchni Ziemi i na pokładach satelitów są
zsynchronizowane. Dzięki temu GPS funkcjonują poprawnie. W systemach globalnego pozycjonowania
uwzględnia się relatywistyczne poprawki wynikające z tego m.in., że zegary na pokładach satelitów i na
powierzchni Ziemi poruszają się z prędkościami równymi, odpowiednio,
VS = 3874 m/s i VZ = 465 m/s
(średnia prędkość zegara na powierzchni Ziemi). Niech ∆τZ oznacza małą wartość czasu upływającego na
zegarach ziemskich, a ∆τS małą wartość czasu odmierzanego na zegarach satelity GPS. Pokazuje się, że:
 v 2  v 2
∆τS
1
=  1 − S2   1 − Z2  = 1 + 2 ( vZ 2 − vS 2 ) , gdzie
c  
c 
∆τ Z
2c

skorzystano ze związku
1 ± x ≅ 1 ± x / 2, x ≪ 1 , słusznego dla wartości x dużo mniejszych od 1. Patrz plik
dostępny pod adresem http://www.if.pwr.wroc.pl/~wsalejda/pop/GPS_DFN_2010.pdf.
17
A) Niech na zegarach ziemskich upłyną 24 godziny, tj. 86 400 s. Na podstawie związku przytoczonego powyżej
oblicz ile sekund upłynie na zegarach satelitarnych? Ile wynosi różnica czasów ∆t (zmierzonych na zegarach
ziemskich i satelitarnych) po upływie jednej doby zmierzonej na zegarach ziemskich. Czy prawdą jest, że
ziemskie zegary spóźniają się względem zegarów satelitarnych?
B) Różnica czasu ∆t z punktu A), gdyby nie była uwzględniona i wyeliminowana, spowodowałaby – po czasie
7·24 h (tydzień) działania GPS – niepewność pomiaru położenia obiektu w przestrzeni daną wzorem ± c·∆t,
co oznacza, że lokalizowany obiekt znajduje się gdzieś w kole na powierzchni Ziemi o promieniu r = c·∆t.
Oblicz wartość r.
C) Na pokładzie satelity poruszającego się z prędkością (3874; 0,0; 0,0) m/s względem spoczywającego
inercjalnego układu odniesienia, leży wzdłuż kierunku ruchu satelity pręt o długości 0,45 m. Wyznacz
długość tego pręta w układzie K poruszającym się z prędkością (465; 0,0; 0,0) m/s względem spoczywającego układu odniesienia.
Niezamieszczenie
stosownych
komentarzy
będzie
traktowane
przy
ocenianiu
jako
brak
rozwiązania/odpowiedzi.
XXV. Przedstaw postulaty szczególnej teorii względności.
W systemach globalnego pozycjonowania (GPS) zegary na powierzchni Ziemi i na pokładach satelitów są
zsynchronizowane. Dzięki temu GPS funkcjonują poprawnie. W systemach globalnego pozycjonowania
uwzględnia się relatywistyczne poprawki wynikające z tego m.in., że zegary na pokładach satelitów i na
powierzchni Ziemi znajdują się w różnych miejscach pola grawitacyjnego Ziemi. Niech ∆τZ oznacza małą
wartość czasu upływającego na zegarach ziemskich znajdujących się w odległości R = 6400 km od środka
Z
Ziemi (tam jest umieszczone źródło pola grawitacyjnego
MZ = 6·1024 kg), a ∆τS małą wartość czasu
odmierzanego na zegarach satelity GPS znajdującego się w odległości R = 26,6 tys. km od środka Ziemi.
S
Pokazuje się, że:
 2GM Z   2GM Z 
∆τS
GM Z GM Z
GM
= 1 −
= 1−
+
= 1+ 2 Z
1 −
2 
2 
2
2
RS c  
RZ c 
∆τ Z
RS c
RZ c
c

gdzie skorzystano ze związku
 1
1 
− ,

 RZ RS 
1 ± x ≅ 1 ± x / 2, x ≪ 1 , słusznego dla wartości x dużo mniejszych
od 1; G = 6,7·10-11 m3/(kg·s2). Patrz plik dostępny pod adresem:
http://www.if.pwr.wroc.pl/~wsalejda/pop/GPS_DFN_2010.pdf
A) Niech na zegarach ziemskich upłyną 24 godziny, tj. 86 400 s. Na podstawie związku przytoczonego powyżej
oblicz ile sekund upłynie na zegarach satelitarnych? Ile wynosi różnica czasów ∆t (zmierzonych na zegarach
ziemskich i satelitarnych) po upływie jednej doby zmierzonej na zegarach ziemskich. Czy prawdą jest, że
ziemskie zegary spóźniają się względem zegarów satelitarnych?
B) Różnica czasu ∆t z punktu A), gdyby nie była uwzględniona i wyeliminowana, spowodowałaby – po czasie
7·24 h (tydzień) działania GPS – niepewność pomiaru położenia obiektu w przestrzeni daną wzorem ± c·∆t.
Oblicz wartość c·∆t.
18
C) Na pokładzie satelity poruszającego się z prędkością (3874; 0,0; 0,0) m/s względem spoczywającego
inercjalnego układu odniesienia, leży zegarek, na którym odmierzono czas ∆t = 1h. Wyznacz wartość tego
czasu ∆t' zmierzony w układzie K poruszającym się z prędkością (465; 0,0; 0,0) m/s względem spoczywającego układu odniesienia.
XXVI.
A) Przedstaw postulaty Bohra modelu atomu wodoru.
B) Wyprowadź wzór En = −
e4 me 1
13,6
= − 2 eV, n = 1,2,3,... określający energię elektronu na n-tej orbicie
2 2
2
n
8ε0 h n
w atomie wodoru oraz podaj interpretację fizyczną wartości 13,6 eV.
C) Korzystając z wyniku punktu B) uzasadnij wzór Balmera
1
1 1 
= const  − 2  , n = 3, 4,5,... oraz opisz jego
λ
4 n 
sens fizyczny.
D) Załóżmy, że niepewność wartości energii, równa odchyleniu standardowemu, elektronu w 5-tym stanie
wzbudzonym wynosi ∆E5 = 10 −6 E5 . Oszacuj minimalna wartość niepewności (odchylenia standardowego) ∆t
czasu życia tego stanu wzbudzonego.
E) Pokaż, że jeśli niepewność (odchylenie standardowe) czasu życia kwantowego stanu wzbudzonego wynosi
∆t, to niepewność (odchylenie standardowe) ∆ν wartości częstotliwości fotonów emitowanych podczas
deaktywacji tego stanu spełnia nierówność ∆ν ≥
1
.
4π ⋅ ∆t
.
F) Korzystając z wyników punktów D) i E) oszacuj minimalną wartość niepewności
(odchylenia stan-
dardowego) ∆ν częstotliwości emitowanych fotonów (∆ν jest nazywana naturalną szerokością linii widmowych) podczas deaktywacji piątego stanu wzbudzonego atomów wodoru.
-----------------------------------------------------------------------------------------XXVII. Fizyka jądrowa.
A) Nieruchomo jądro neodymu ulega rozpadowi α i powstaje jądro ceru, a schemat rozpadu ma następującą postać:
144
60
4
Nd → 140
58 Ce + 2 He + E ,
gdzie E jest energią wydzieloną podczas rozpadu. Masy jąder biorących udział w rozpadzie wynoszą:
mNd = 143,9099 ⋅ u, mCe = 139,9053 ⋅ u, mHe = 4,0026 ⋅ u,
u = 1,6605 ⋅ 10−27 kg = 931,4940
MeV
.
c2
A.1) Uzasadnij, że podczas opisanego rozpadu wyzwalana jest energia E = 1,863 MeV = 2.981·10
≅ 1,6·10
-19
-13
J; przyjąć, że
1 eV
J.
A.2) Zakładając, że elementy rozpadu mają prędkości znacznie mniejsze od prędkości światła (rozpad nierelatywistyczny),
uzasadnij, że zarówno jądro ceru jak i cząstka α mają po rozpadzie wartości pędów dane wzorem:
19
pCe = pHe =
2 ⋅ E ⋅ mHe ⋅ mCe
.
mHe + mCe
A3) W wyniku bombardowania jądra berylu cząsteczkami α można otrzymać jądra węgla oraz jedną z cząstek mikroświata. Wzór
tej reakcji jądrowej ma postać
9
4
Be + ......α → 126 C +...... ... .
Podaj na otrzymanej kartce papieru pełny zapis opisanej reakcji jądrowej.
A4) Przeprowadzenie reakcji jądrowej opisanej w A3) wymaga zastosowania cząstek α o dostatecznie dużej energii kinetycznej.
Jaka powinna być co najmniej energia kinetyczna cząsteczki α, aby mogła zbliżyć się do nieruchomego jądra berylu na odległość
2·10-15 m? Dane są: wartość ładunku elementarnego q ≅ 2·10-19 C, masa protonu równa masie neutronu mP ≅ 2·10-27 kg, k =
1/(4πε0) ≅ 1010 N·m2/C2.
A5) Wyznacz prędkość początkową jaką mają cząsteczki α, o których jest mowa w zagadnieniu A4)?
Uwaga: Odpowiedzi liczbowe/wyprowadzone wzory należy koniecznie opatrzyć stosownymi komentarzami, których brak
zdyskwalifikuje wyniki liczbowe/wyprowadzone wzory
-------------------------------------------------------------------------------------------------------------------------------------------XXVIII. A) Jedenastu studentów zmierzyło niezależnie rozmiary liniowe prostokątnego pola ziemi. Wyniki pomiarów
szerokość
długość zapisywali w tabeli znajdującej się obok. Oblicz na podstawie wykonanych pomiarów
Lp.
wartość powierzchni S tego pola oraz odchylenie kwadratowe otrzymanej wartości S.
(m)
(m)
1
45,5
57,8
B) Okres drgań wahadła fizycznego jest obliczany na podstawie wzoru
2
45,7
57,4
J
3
45,3
57,9
T = 2π
, gdzie J – wyznaczony doświadczalnie moment bezwładności
4
45,1
57,2
mgd
5
45,8
57,5
wahadła, m – wyznaczona doświadczalnie masa wahadła, g – wyznaczona
6
45,6
57,6
doświadczalnie
w miejscu pomiaru wartość przyspieszenia ziemskiego, d –
7
45,9
57,4
wyznaczona doświadczalnie odległość punktu zawieszenia od środka masy wahadła.
8
44,9
57,9
Wyprowadź wzór pozwalający oszacować niepewność względną pojedynczego
9
46,1
57,5
10
57,6
44,6
∆T
pomiaru
przy założeniu, że znane są niepewności pomiarów: ∆J, ∆m, ∆g i ∆d
11
45.7
57,4
oraz wartości zmierzonych wielkości, tj.
T
J , m, g ,i d .
C) Opisz, jak należy szacować średnią wartość
∆T
T
, jeśli każdą z wielkości: J, m, g i d wyznaczono n-krotnie
niezależnymi pomiarami?
D) Opisz jak szacujemy niepewność wartości średniej zmierzonej wielokrotnie przyrządem pomiarowym wielkości
fizycznej, jeśli otrzymane wyniki pomiarów nie wykazują zauważalnego rozrzutu?
E) Opisz jak szacujemy niepewność wartości średniej zmierzonej wielokrotnie przyrządem pomiarowym wielkości
fizycznej, jeśli uwzględniamy niepewność statystyczną (wyniki serii pomiarów wykazują zauważalny rozrzut) oraz
niepewność użytego przyrządu pomiarowego?
Czytaj opracowanie dostępne na stronie: http://www.if.pwr.wroc.pl/~wsalejda/an_niep/analiza_niepewnosci_2009.pdf
W. Salejda
Wrocław, 25 lutego 2015
20
Dodatek.
Dany jest obwód
Oblicz natężenia i kierunki płynących prądów w elementach obwodu przedstawionego powyżej. W punkcie c
potencjał jest równy zeru. Oblicz wartości potencjałów w punktach obwodu od a do f.
Rozwiązanie:
1) Zadajemy kierunek obchodzenia 2 wybranych oczek (pętli) zgodny z ruchem wskazówek zegara.
2) Zaznaczamy (zakładamy dość dowolnie) kierunki przepływu prądu w obu pętlach.
3) Liczymy kolejno:
a. Opór zastępczy oporników 3Ω i 6Ω połączonych równolegle, co daje 2Ω.
b. I reguła Kirchhoffa w zastosowaniu do węzła b prowadzi do równości: I=I1+I2,
c. II reguła Kirchhoffa w zastosowaniu do pętli abefa daje: 18V-I·12Ω- I1·6Ω=0, tj. 18V-I·12Ω-(I-I2)·6Ω=0; „dzielimy” przez 6Ω
dostajemy: 3A-3I+I2=0; komentarz: znak plus przy SEM jest dodatni, ponieważ kierunek przechodzenia SEM jest zgodny ze
wzrostem potencjału (idziemy od mniejszego (-) do wyższego potencjału (+) baterii); spadki napięć na obu opornikach są
poprzedzone znakiem (-) ponieważ, kierunek obchodzenia jest zgodny z przyjętym kierunkiem przepływu prądu przez oba
oporniki;
d. II reguła Kirchhoffa w zastosowaniu do pętli bcdeb pozwala zapisać równość: -3I2 Ω + 21V - 2I2Ω + 6I1Ω = -3I2Ω + 21V 2I2Ω + 6(I - I2)Ω = 0, skąd po prostych przekształceniach otrzymujemy: 21A + 6I - 11I2=0.
e. Rozwiązując układ 2 równań: 3A - 3I + I2 = 0 i 21A + 6I - 11 I2 = 0, wyznaczamy I = 2A, I2 = 3A i I1 = -1A
f. Obliczamy teraz spadki napięć na poszczególnych oporach: ∆V3Ω = 9V, ∆V2Ω = 6V; ∆V6Ω = -6V, ∆V12Ω= 24V. Pozwala to
sporządzić wykres układu, pokazany na końcu Dodatku.
g. Policzymy obecnie prądy płynące w opornikach połączonych równolegle. Ponieważ znamy spadki napięcia na
każdym oporniku, to z prawa Ohma wyznaczamy natężenia: I3Ω = 2A, I6Ω = 1A.
21
h. Teraz możemy obliczać potencjały poszczególnych punktów schematu analizowanego układu:
Vd = 0 + 21V = 21V;
Ve = 0 + 21V - 6V = 15V;
Vf = Ve = 15V;
Va = Vf + 18V= 33V;
Vb = Va - 24V= 9V.
Poniżej graficzna ilustracja będąca odpowiedzią na postawione pytania. Zwraca uwagę poprawny kierunek przepływu
prądu przez opór o wartości 6Ω, który płynie w rzeczywistości w przeciwnym kierunku od założonego, co potwierdzają obliczone
wartości potencjałów w punktach b i e.
Zauważmy, że prąd płynie w oporniku 6 Ω w przeciwnym kierunku od założonego, na co wskazuje ujemna jego
wartość wyznaczona z rozwiązania układu równań w pkt. e.
W.Salejda
Wrocław, 25 lutego 2015
22
Karta pisemnego egzaminu (20 VI 2014) do kursu Fizyka dla studentów Wydz. Inż. Środ. Kierunek Inż. Środ.
Imię i nazwisko ……………………………..……………….…… Nr albumu: ……………..………...
Instrukcja. Osoba zdająca wpisuje CZYTELNIE ww. dane, pisemne odpowiedzi opracowuje na wybrane co najwyżej 5
zagadnień na oddzielnych arkuszach papieru, które opatruje nazwiskiem i numerem zadania.
………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………….
I. A) Opisz interpretację fizyczną zasad zachowania pędu dla pojedynczego ciała* (3 pkt) oraz układu N ciał* (4 pkt) podając warunki
ich stosowalności w każdym z przypadków (4 pkt).
B) W drewniane wahadło balistyczne o masie m2 = 14,0 kg uderzył
lecący poziomo z prędkością o wartości 800 m/s pocisk o masię
m1 = 0,008 kg, przebił je i wyleciał z prędkością o wartości
vk
= 84 m/s. Wyznacz wysokość h, na którą wzniesło się wahadła
(patrz rysunek obok) (5 pkt).
C) Spoczywające jądro neodymu uległo rozpadowi na cząstkę α i jądro ceru według następującego schematu:
144
60
4
Nd → 140
58 Ce + 2 He + E , gdzie E jest energią wydzieloną podczas rozpadu. Zakładając, że elementy
rozpadu mają prędkości znacznie mniejsze od prędkości światła (nierelatywistyczny rozpad), uzasadnij, że
wektor pędu jądra ceru P i wektor pędu cząstki α p po rozpadzie spełniają równość P + p = 0 (4 pkt).
……………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………….
II. A) Opisz interpretację fizyczną:
A1) Drugiej zasady dynamiki ruchu obrotowego bryły sztywnej* obracającej się
wokół ustalonej osi obrotu będącej jej osią symetrii (6 pkt.)
A2) Zasady zachowania momentu pędu bryły sztywnej* oraz przedstaw warunki jej
stosowalności. (6 pkt.)
B) Znane są masy m, M, moment bezwładności I krążka, jego promień R oraz współczynnik tarcia f ciała o masie m położonego na powierzchni (patrz rys. po prawej
stronie).
B1) Na własnoręcznie sporządzonym rysunku przedstaw diagram sił przyłożonych
do obu ciał i krążka (4 pkt).
B2) Wyznacz przyspieszenie masy M traktując jako dane M, m, współczynnik tarcia f masy m o poziomą
chropowatą powierzchnię, moment bezwładności I, promień krążka R, przyspieszenie ziemskie g (4 pkt).
…………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………….
III. A) Podaj treść zasady zachowania energii mechanicznej* (6 pkt). Określ, przy jakich warunkach można ją
stosować. (6 pkt).
B) Samochód, którego wektor prędkości początkowej ma wartość v0 hamuje na drodze o długości s0. Jeśli ten
samochód jadący z prędkością n·v0 (n > 1) zacznie hamować na tej samej drodze, to o ile razy wzrośnie* jego
droga hamowania? (4 pkt).
C) Z wysokości H nad poziomem ziemi wyrzucono pod różnymi kątami αi (1 ≤ i ≤ N) do poziomu N metalowych
kulek z miedzi o różnych masach mi. Uzasadnij stwierdzenie*: Jeśli pominąć opory powietrza, to każda
z wyrzuconych kulek będąc na wysokości h = H/9 miała taką samą, co do wartości, prędkość i różne wektory
prędkości. Przy jakim/jakich założeniach stwierdzenie jest prawdziwe? (4 pkt).
* Wyprowadzenia/zastosowane wzory, odpowiedzi liczbowe należy skomentować/objaśnić, ponieważ ich brak zdyskwalifikuje odpowiedź.
23
IV. A) Opisz sens fizyczny prawa indukcji elektromagnetycznej Faraday’a*6 pkt) oraz reguły Lenza* (4 pkt).
B) Rys. A1 przedstawia mały fragment długiego przewodnika z prądem o natężeniu I, którego kierunek przepływu pokazuje strzałka. W pobliżu tego przewodnika znajduje się prostokątna miedziana ramka. Opisz* co najmniej 3 różne ruchy ramki, w trakcie których wyindukowany zostanie w niej prąd elektryczny (3 pkt). Wyjaśnij*
dlaczego w ramce indukuje się wówczas prąd elektryczny? (2 pkt).
C) Miedziany drut PS o dłua
P
L
B
I
Rys. A2
Rys. A1
S
b
gości L jest przesuwany po
poziomych
miedzianych
prętach, jak na rys. A2, w jednorodnym polu magnetycznym z prędkością o
wartości
V w kierunku
wskazanym strzałką.
Początkowe położenie drutu PS, dla t = 0 sek., pokrywało się z linią przerywaną ab. Zakładając, że w chwili
początkowej prędkość drutu PS była równa zeru, dla chwili czasu t > 0:
C1) Określ* kierunek przepływu prądu I(t) w układzie z rys. A2 (1 pkt).
C2) Wyznacz chwilową moc* prądu P(t) w układzie z rys. A2 zakładając, że dany jest opór R(t) obwodu w chwili
czasu t. (2 pkt).
D) Opisz* rodzaj konwersji energii, z którą mamy do czynienia na rys. A2 (2 pkt).
……………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………….
V. A) Funkcja x ( t ) = 0,01 ⋅ sin ( 5 ⋅ t + π 3) opisuje w SI drgania ciała o masie 0,6 kg podwieszonego
do sprężyny o nieznanym współczynniku sprężystości k. Ile wynosi:
A1) Okres drgań* (1 pkt), wartość* k (1 pkt), energia mechaniczna* tych drgań (1 pkt)?
B) Masa planety Mars jest 9 razy mniejsza o masy Ziemi a jego promień jest 2 razy mniejszy od promienia Ziemi.
Uzasadnij*, że stosunek okresów drgań wahadeł matematycznych o jednakowych długościach wykonujących
drgania na powierzchni Marsa i Ziemi wynosi* TMarsa TZiemi ≅ 3 2 (4 pkt).;
C) Przedstaw definicję fali mechanicznej (sprężystej) *. Jakie warunki* muszą być spełnione, aby możliwe było
rozchodzenie się fal sprężystych? (4 pkt).
D) Fala poprzeczna y(x, t) = 3·10-4·sin(300·t – 0,1·x) biegnie w naciągniętej strunie.
D1) Opisz sens fizyczny*użytych we wzorze fali wielkości fizycznych podając ich jednostki miar w SI (5 pkt.).
D2) Ile wynosi: a) częstotliwość*(1 pkt), długość*(1 pkt), prędkość fazowa* (1 pkt) fali oraz maksymalna
prędkość* fragmentów struny, w której ta fala biegnie (1 pkt)?
------------------------------------------------------------------------------------------------------------------------------VI. DODATKOWE. Opisz interpretację fizyczną II zasady dynamiki Newtona* (10 pkt).
A) Na kuliste (o średnicach ≤ 10-4 m) krople rosy, spadające w nieruchomym powietrzu pionowo w dół, działa
siła oporu o wartości F = 6πηrv, gdzie η – lepkość powietrza, v – prędkość kropli, r – promień kropli.
A1) Wyjaśnij* dlaczego krople rosy rozpoczynające spadek najpierw poruszają się ruchem jednostajnie
zmiennym a następnie opadają ruchem jednostajnym prostoliniowym (4 pkt).
A2) Przyjmując η = 2·10-5N·s/m, gęstość wody ρ = 1000 kg/m3, r = 5·10-5 m, g = 10 m/s2, zaniedbując siłę wyporu
powietrza, oblicz* wartość prędkości w ruchu jednostajnym prostoliniowym (4 pkt).
A3) Ile czasu* spada kropla rosy z wysokości 800 m, przy założeniu, że opada ruchem jednostajnym prostoliniowym, który obserwuje się po przebyciu przez kroplę zaledwie kilka metrów (2 pkt).
W. Salejda
Wrocław, 20 czerwca 2014 r.
*Udzielając odpowiedzi należy opisać znaczenie symboli wielkości fizycznych użytych we wzorach podając ich jednostki miar w SI.
24
Karta pisemnego egzaminu (27 VI 2014) do kursu Fizyka dla studentów Wydz. Inż. Środ. Kierunek Inż. Środ.
Imię i nazwisko ……………………………..……………….…… Nr albumu: ……………..………...
Instrukcja. Osoba zdająca wpisuje CZYTELNIE ww. dane a pisemne odpowiedzi opracowuje na oddzielnych kartkach
papieru formatu A-4, które opatruje nazwiskiem i numerem zadania.
…………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………….
I. A) Opisz interpretację fizyczną zasad zachowania pędu dla pojedynczego ciała* (3 pkt) oraz układu N ciał* (4 pkt) podając warunki ich
stosowalności w każdym z przypadków (4 pkt).
B) W wahadło balistyczne o masie m2 uderzył lecący poziomo
z prędkością v0 pocisk o masię m1, przebił je i wyleciał z prędkością o
nieznanej wartości vk. Wyznacz vk, jeśli znana jest wysokość h, na którą
wzniosło się wahadło (patrz rys. obok) (5 pkt).
C) Spoczywające jądro neodymu uległo rozpadowi na cząstkę α i jądro ceru według następującego schematu:
144
60
4
Nd → 140
58 Ce + 2 He + E , gdzie E jest energią wydzieloną podczas rozpadu. Zakładając, że elementy
rozpadu mają prędkości znacznie mniejsze od prędkości światła (nierelatywistyczny rozpad), uzasadnij, że
wektor pędu P jądra ceru i wektor pędu p cząstki α po rozpadzie spełniają równość P + p = 0 (4 pkt).
……………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………….
II. A) Przedstaw interpretację fizyczną:
A1) Zasady zachowania energii mechanicznej ciała oraz przedstaw warunki jej stosowalności (6 pkt).
A2) Zasady zachowania momentu pędu bryły sztywnej* oraz przedstaw warunki jej stosowalności (6 pkt).
B) Znane są: masy m, M, moment bezwładności I krążka, jego promień R oraz współczynnik tarcia f ciała o masie m położonego na powierzchni (patrz rys. po prawej stronie) oraz
przyspieszenie ziemskie g.
B1) Na własnoręcznie sporządzonym rysunku przedstaw diagram sił przyłożonych do obu ciał i krążka (4 pkt).
B2) Wyznacz przyspieszenie masy M (4 pkt).
………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………….
III. A) Opisz sens fizyczny prawa indukcji elektromagnetycznej Faraday’a* (6pkt) oraz reguły Lenza* (4pkt).
B) Rys. A1 przedstawia mały fragment długiego przewodnika z prądem o natężeniu I, którego kierunek przepływu pokazuje
strzałka. W pobliżu tego przewodnika znajduje się prostokątna miedziana ramka. Wyjaśnij* dlaczego zbliżając lub oddalając
ramkę z rys. A1. do przewodnika wyindukowany zostanie w niej prąd elektryczny (3 pkt)?
a
C) Miedziany drut PS o długości L jest
P
L
I
•B
Rys. A2
Rys. A1
S
b
przesuwany po poziomych miedzianych
prętach, jak na rys. A2, w jednorodnym
polu magnetycznym z prędkością o
wartości V w kierunku wskazanym
strzałką. Pole magnetyczne jest
skierowane przed kartkę.
Początkowe położenie drutu PS, dla t = 0 sek., pokrywało się z linią przerywaną ab.
C1) Określ* kierunek przepływu prądu I(t) w układzie z rys. A2 dla t > 0 (2 pkt).
C2) Wyznacz chwilową wartość natężenia* prądu I(t) w układzie z rys. A2 dla t > 0, zakładając, że dany jest opór R(t) obwodu
w chwili czasu t. (3 pkt).
E) Opisz* rodzaj konwersji energii, z którą mamy do czynienia na rys. A2 (2 pkt).
……………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………….
*Udzielając odpowiedzi należy opisać znaczenie symboli wielkości fizycznych użytych we wzorach podając ich jednostki miar w SI.
25
IV. A) Funkcja x ( t ) = 0,02 ⋅ sin ( 5π ⋅ t + π 6) opisuje w SI drgania ciała o masie 0,1 kg podwieszonego do sprężyny o nieznanym współczynniku sprężystości k. Ile wynosi:
A1) Okres drgań* (1 pkt), wartość* k (1 pkt), energia mechaniczna* tych drgań (1 pkt)?
B) Przedstaw definicję fali mechanicznej (sprężystej)* (4 pkt). Jakie warunki* muszą być spełnione,
aby możliwe było rozchodzenie się fal sprężystych? (2 pkt).
C) Fala poprzeczna y(x, t) = 2·10-4·sin(300π·t – 0,1π·x) biegnie w naciągniętej strunie.
C1) Opisz sens fizyczny* użytych we wzorze fali wielkości fizycznych podając ich jednostki miar w SI (5 pkt).
C2) Ile wynosi: a) częstotliwość* (1 pkt), długość* (1 pkt), prędkość fazowa* (1 pkt) fali oraz maksymalna
prędkość* fragmentów struny, w której ta fala biegnie (1 pkt)?
D) Podczas mgły syrena stojącego nieruchomo statku wysyła sygnały dźwiękowe o częstotliwości 3 kHz. Rybak
na kutrze płynącym w stronę statku odbiera dźwięki syreny o częstotliwości 3,05 kHz. Przyjmując, że prędkość
dźwięku we mgle wynosi 330 m/s, oblicz wartość prędkości kutra (2 pkt).
………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………….
V. A) Opisz sens fizyczny praw Keplera* (6 pkt). Wyjaśnij*, dlaczego wartość prędkości danej planety na orbicie
okołosłonecznej nie jest stała (4 pkt)?
B) Masa M Marsa planety Mars stanowi 10% masy Ziemi, a promień Marsa jest dwa razy mniejszy od promienia
Ziemi. Wyznacz:
B1) Wartość gZ/gM*, gdzie gZ – przyspieszenie ziemskie, gM – przyspieszenie marsjańskie (4 pkt).
B2) Wyznacz stosunek okresów* TZ TM drgań wahadeł matematycznych o tych samych długościach wahających się, na powierzchni, odpowiednio, Ziemi i Marsa (4 pkt).
B3) Ile razy pierwsza prędkość kosmiczna dla Marsa jest większa/mniejsza* od pierwszej prędkości kosmicznej
dla Ziemi (4 pkt)?
B4) Prędkości punktów na równiku Ziemi wynoszą 460 m/s, a na równiku Marsa 240 m/s. Uzasadnij*, że czas
trwania marsjańskiej doby tMarsa stanowi (23/24)⋅tZiemi i wynosi 23 godziny (4 pkt).
B5) Pokaż*, że odległość d geostacjonarnego satelity Marsa od środka tej planety spełnia równość
d 3 = GM Marsa ( tMarsa ) 4π 2 (6 pkt).
2
………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………….
VI. A) Opisz sens fizyczny zasad dynamiki Newtona* (5 pkt) oraz użytych do ich matematycznego zapisu
wielkości fizycznych* (3 pkt) podając ich jednostki miary (3 pkt).
B) Na ciało spadające pionowo w dół w polu grawitacyjnym Ziemi działa siła F oporu zależna od prędkości V, a
jej wartość wynosi F = CρV2S/2, gdzie ρ – gęstość powietrza, S – pole przekroju prostopadłego ciała w stosunku
do wektora prędkości, C – współczynnik zależny od kształtu ciała. Piłeczka pingpongowa ma masę m
i promień r. Wyznacz prędkość z jaką upuszczona swobodnie piłeczka będzie spadała ruchem jednostajnym
prostoliniowym (przyjmujemy, że powietrze jest nieruchome) (5 pkt).
C) Rzucono pod kątem α do poziomu ziemi kulkę o masie m z prędkością początkową o wartości v0. Zaniedbując
opory powietrza wyznacz/uzasadnij:
C1) Tor ruchu kulki, tj. zależność y(x), gdzie y – wysokość nad powierzchną ziemi, x – odległość ciała od punktu
wyrzutu zakładając, że ciało wyrzucono z początku prostokątnego układu współrzędnych (5 pkt).
C2) Czas wznoszenia się kulki na największą wysokość (2 pkt).
C3) Uzasadnij prawdziwość twierdzenia: Energia mechaniczna rzuconej przy powierzchni ziemi kulki o masie m
w każdym punkcie toru wynosi m(v0)2/2 (6 pkt).
Wrocław, 27 czerwca 2014 r
W. Salejda
*Udzielając odpowiedzi należy opisać znaczenie symboli wielkości fizycznych użytych we wzorach podając ich jednostki miar w SI.
26