tr - Zaliczaj.pl

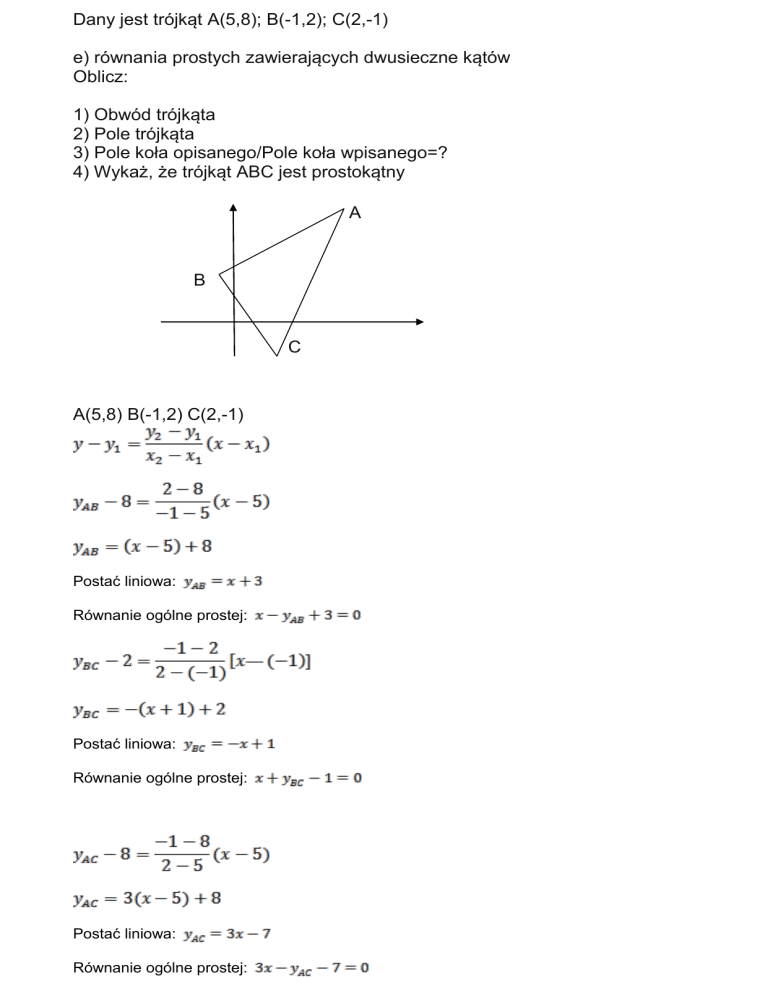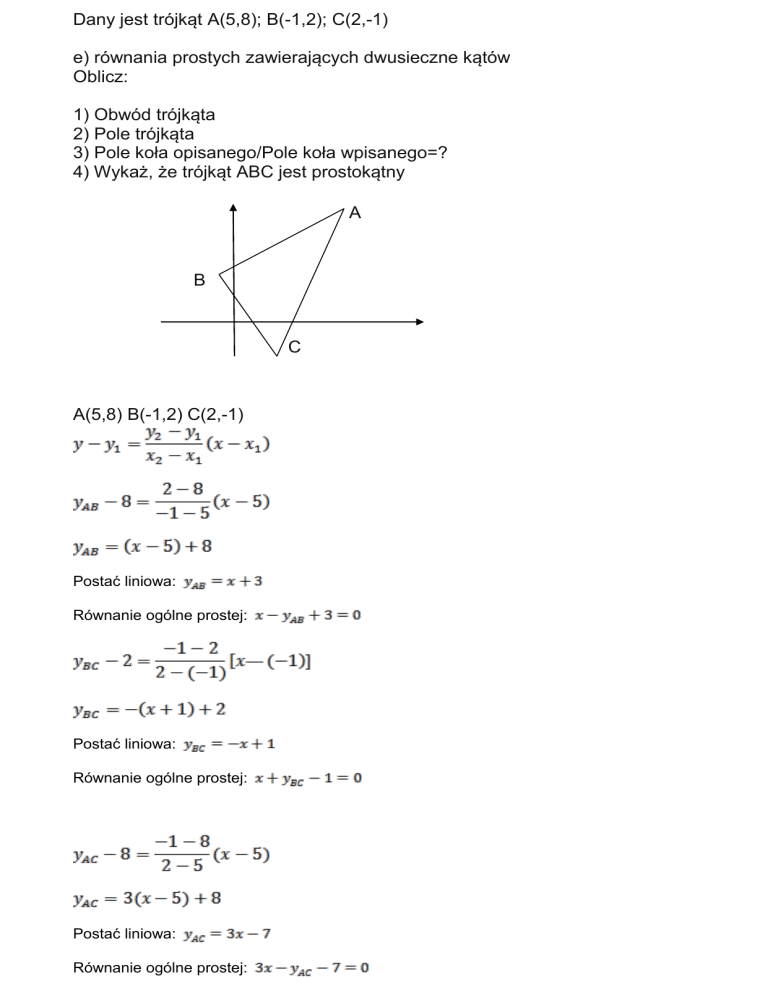
Dany jest trójkąt A(5,8); B(-1,2); C(2,-1)
e) równania prostych zawierających dwusieczne kątów
Oblicz:
1) Obwód trójkąta
2) Pole trójkąta
3) Pole koła opisanego/Pole koła wpisanego=?
4) Wykaż, że trójkąt ABC jest prostokątny
A
B
C
A(5,8) B(-1,2) C(2,-1)
Postać liniowa:
Równanie ogólne prostej:
Postać liniowa:
Równanie ogólne prostej:
Postać liniowa:
Równanie ogólne prostej:
Dwusieczna kąta przy wierzchołku A to prosta = zbiór punktów równo oddalonych od prostych
.
Analogicznie określam dwusieczne pozostałych kątów.
Korzystam z ogólnych równań prostych:
Odległość punktu P(xP ,yP) od prostej o równaniu ogólnym: Ax + By + C = 0:
Dwusieczna kąta przy wierzchołku A:
Ponieważ odległości od prostej AB i AC mają być równe ( z definicji dwusiecznej), to na podstawie
równań ogólnych tych prostych porównuję (jako równe) odległości punktów od tych prostych:
W wyniku otrzymalibyśmy dwie proste (prostopadłe do siebie). Można uprościć postępowanie,
żeby nie przeprowadzać żmudnych i skomplikowanych obliczeń, stosując następującą procedurę.
Musimy pozbyć się wartości bezwzględnych. Przy rozwiązywaniu równań z wartością bezwzględną,
rozważa się wszystkie możliwości: kiedy wyrażenia pod wartością bezwzględną przyjmują wartości
dodatnie a kiedy ujemne. Aby tego uniknąć wybieram współrzędne jakiegoś punktu, który leży na
pewno w interesującej nas przestrzeni pomiędzy prostymi AB i AC, np. punkt o współrzędnych
(0,0).
Podstawiam do równania ogólnego prostej AB:
1∙ 0 – 1 ∙ 0 + 3 = 3 > 0
Interesująca nas półpłaszczyzna leżąca poniżej prostej AB spełnia nierówność x – y + 3 > 0, a więc
po opuszczeniu wartości bezwzględnej nie zmieniamy znaków przy poszczególnych wyrazach.
Podobnie postępuję dla prostej AC:
3 ∙0 – 1 ∙ 0 – 7 = - 7 < 0
W tym przypadku spełniona jest nierówność: 3x –y – 7 < 0 więc opuszczając znak wartości
bezwzględnej musimy zmienić znaki przy poszczególnych wyrazach.
Otrzymujemy równanie:
Po wymnożeniu „na krzyż”:
Równanie ogólne dwusiecznej kąta przy wierzchołku A:
Równanie liniowe:
Wyznaczenie dwusiecznej kąta przy wierzchołku B:
Podobnie jak poprzednio, żeby pozbyć się znaków wartości bezwzględnej wybieram
punkt, należący do przestrzeni ograniczonej tymi prostymi, w której poszukujemy
dwusiecznej, np. punkt o współrzędnych (2,0).
Dla prostej AB:
2 – 0 + 3 = 5 > 0 czyli opuszczając znak wartości bezwzględnej, nie zmieniamy znaków
poszczególnych składników
Dla prostej BC:
2 + 0 - 1 = 1 > 0 czyli opuszczając znak wartości bezwzględnej, również nie zmieniamy znaków
poszczególnych składników.
Równanie dwusiecznej kąta przy wierzchołu B (prosta pozioma – równoległa do osi OX):
Wyznaczenie dwusiecznej kąta przy wierzchołku C:
Podobnie jak poprzednio, żeby pozbyć się znaków wartości bezwzględnej wybieram punkt,
należący do przestrzeni ograniczonej tymi prostymi, w której poszukujemy dwusiecznej, np. punkt
o współrzędnych (2,0).
Dla prostej BC:
czyli opuszczając znak wartości bezwzględnej, nie zmieniamy znaków
poszczególnych składników.
Dla prostej AC:
∙
czyli opuszczając znak wartości bezwzględnej, zmieniamy znaki
poszczególnych składników.
Postać ogólna dwusiecznej kata przy wierzchołku C:
Równanie liniowe dwusiecznej:
1) Obliczenie obwodu trójkąta:
A(5,8) B(-1,2) C(2,-1)
|AB|=
|AC|=
|BC|=
2) Obliczenie pola trójkąta:
Z liniowych postaci prostych, zawierających boki trójkąta widać, że proste AB i i BC:
są prostopadłe, gdyż współczynniki a przy x łączy zależność:
.
Mamy więc trójkąt prostokątny o przyprostokątnych |AB| i |BC|.
3) Promień okręgu wpisanego w trójkąt:
Pole koła wpisanego w trójkąt:
Promień okręgu opisanego na trójkącie to połowa przeciwprostokątnej:
Pole koła opisanego na trójkącie:
4) Przy obliczaniu pola trójkąta wykazaliśmy, że jest on prostokątny:
„Z liniowych postaci prostych, zawierających boki trójkąta widać, że proste AB i i BC:
są prostopadłe, gdyż współczynniki a przy x łączy zależność:
Mamy więc trójkąt prostokątny o przyprostokątnych |AB| i |BC|.”
Ponadto sprawdzając Twierdzenie Pitagorasa:
.