Estymatory punktowe z próby i ich własności

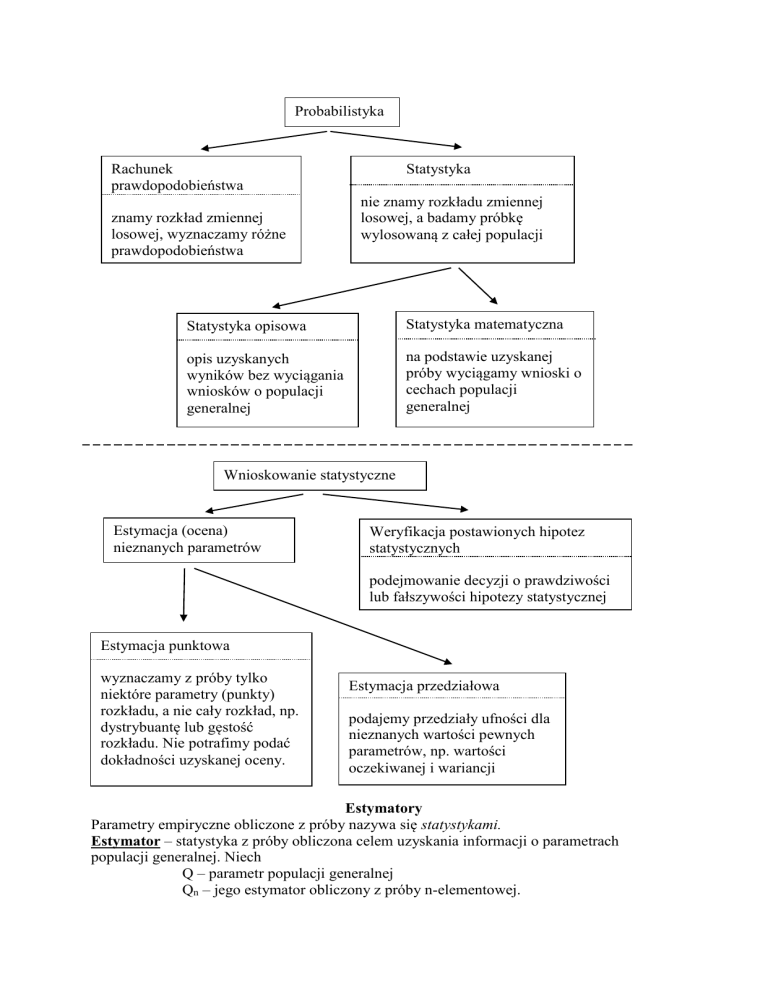
Probabilistyka
Rachunek
prawdopodobieństwa
znamy rozkład zmiennej
losowej, wyznaczamy różne
prawdopodobieństwa
Statystyka
nie znamy rozkładu zmiennej
losowej, a badamy próbkę
wylosowaną z całej populacji
Statystyka opisowa
Statystyka matematyczna
opis uzyskanych
wyników bez wyciągania
wniosków o populacji
generalnej
na podstawie uzyskanej
próby wyciągamy wnioski o
cechach populacji
generalnej
Wnioskowanie statystyczne
Estymacja (ocena)
nieznanych parametrów
Weryfikacja postawionych hipotez
statystycznych
podejmowanie decyzji o prawdziwości
lub fałszywości hipotezy statystycznej
Estymacja punktowa
wyznaczamy z próby tylko
niektóre parametry (punkty)
rozkładu, a nie cały rozkład, np.
dystrybuantę lub gęstość
rozkładu. Nie potrafimy podać
dokładności uzyskanej oceny.
Estymacja przedziałowa
podajemy przedziały ufności dla
nieznanych wartości pewnych
parametrów, np. wartości
oczekiwanej i wariancji
Estymatory
Parametry empiryczne obliczone z próby nazywa się statystykami.
Estymator – statystyka z próby obliczona celem uzyskania informacji o parametrach
populacji generalnej. Niech
Q – parametr populacji generalnej
Qn – jego estymator obliczony z próby n-elementowej.
Zauważmy, że Qn=f(x1, x2, …, xn) jest zmienną losową, Q nie jest.
Estymator może być:
PQn  Q     1
zgodny:
lim
n
nieobciążony:
E(Qn)=Q
gdy E(Qn)jest różne od Q, to estymator jest obciążony, a ich różnicę nazywamy
obciążeniem estymatora
najbardziej efektywny:
jest to taki estymator nieobciążony, który ma najmniejszą
wariancję spośród wszystkich estymatorów .
Estymatory punktowe z próby i ich własności
Parametr
estymowany
Wartość oczekiwana
Estymator
wzór
nazwa
Wartość średnia
zgodny
nieobciążony
najbardziej efektywny
(roz. normalny)
1 n
2
 xi   
i

1
n
1.
2.
3.
1 n
2
 x i  x 
n i 1
1 n
2
Sˆ x2   x i  x 
i

1
n
S x  S x2
1.
zgodny
nieobciążony
najbardziej efektywny
(roz. normalny)
zgodny
1.
zgodny
2.
nieobciążony
1.
zgodny
Sˆ x  Sˆ x2
1.
zgodny
x
1 n
 xi
n i 1
S x2 
Wariancja
Odchylenie
standardowe
Wariancja z próby
Odchylenie
standardowe z próby
własności
1.
2.
3.
S x2 
Estymatory oznaczone ‘daszkiem’ stosujemy dla małej próby (n<30).