2010 ETAP 1

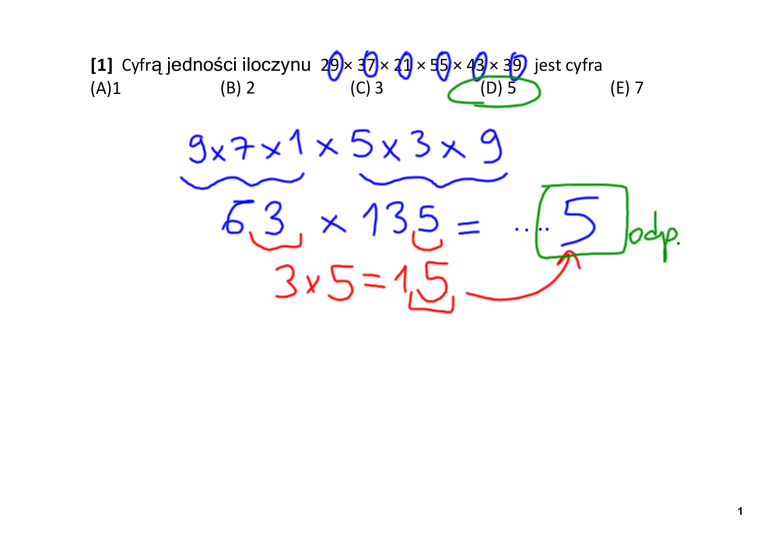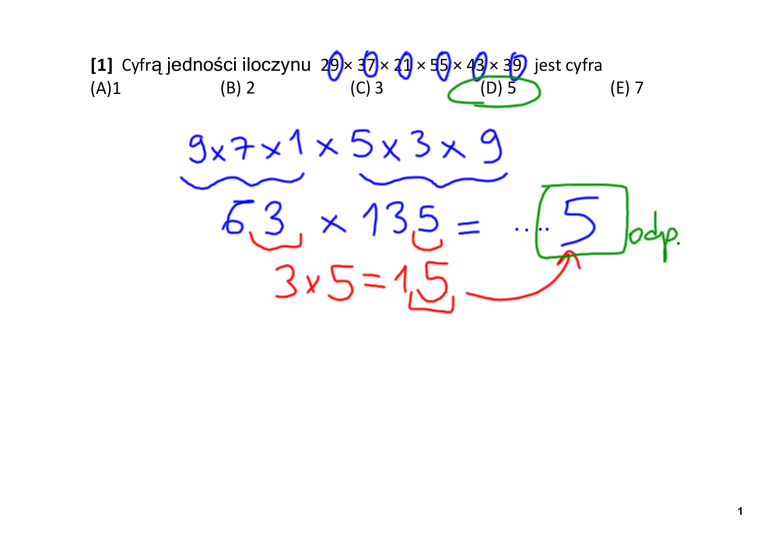
[1] Cyfrą jedności iloczynu 29 × 37 × 21 × 55 × 43 × 39 jest cyfra (E) 7
(D) 5 (C) 3 (B) 2 (A)1 1
[2] Ile cyfr wystąpi w zapisie ułamka w postaci ułamka dziesiętnego :
(E) 5
(D) 4 (C) 3 (B) 2 (A) 1 2
[3] Liczba dwucyfrowych liczb pierwszych, zapisanych za pomocą cyfr 2;3;5;7; jest równa
(E) 6
(D) 5 (C) 4 (B) 2 (A) 1 3
[4] Suma cyfr liczby 5104 × 452 jest równa :
(A) 1 (B) 2 (C) 3 (D) 4 (E) 5
4
[5] Na ile sposobów możemy ustawić litery słowa SIMPLUS, jeżeli w ustawieniu ma wystąpić słowo PLUS (A) 4 (B) 8 (C) 16 (D) 48 (E) 24
5
[6] Wiadro wypełnione jest wodą w 60 %. Jeżeli usuniemy 20 % tej wody, w wiadrze zostanie 192 ml wody. Maksymalna pojemność wiadra wynosi (E) 400
(D) 350 (C) 325 (B) 300 (A) 275 6
[7] Pięć jednakowych kwadratów o długości boku równej 2 cm ułożono jak na rysunku. Punkt M jest środkiem odcinka PQ. Pole zacieniowanej części jest równe ﴾ w cm2 )
(A) 14 (B) 12 (C) 10 (D) 8 (E) 6
7
[8] W podanym obok diagramie liczba w dowolnym polu jest równa sumie liczb w polach położonych bezpośrednio pod danym polem. Wartość liczby, oznaczonej litera A jest równa
(A) 88 (B) 67 (C) 21 (D) 97 (E) 12
8
[9] Jeżeli ; oraz a + c = 30 , to wartość liczby b jest równa
(A) 3 (B) 18 (C) 12 (D) 60 (E) 10
9
[10] Samochód jedzie ze stałą prędkością dwie godziny z miasta SIMcity do miasta PLUScity.
Jeżeli prędkość obniżymy o 30 km/h, to droga zajmie 3,2 godziny. Odległość między SIMcity i PLUScity wynosi
(E) 160
(D) 140 (C) 120 (B) 90 (A) 30 10
[11] ABCD oraz BJKL to dwa kwadraty o boku długości 8 cm. Punkt M jest środkiem odcinka AD oraz odcinka JK. Pole sześciokąta BCDMKL wynosi (w cm2 )
(A) 64 (B) 80 (C) 96 (D) 112 (E) 128
11
[12] Suma jedenastu kolejnych liczb parzystych wynosi p. Wtedy największa z tych liczb równa jest
12
[13] ABCD jest pięciokątem foremnym. Miara kąta zaznaczonego x jest równa
(A) 18° (B) 27° (C) 33° (D) 36° (E) 42°
13
[14] Rozważmy wszystkie liczby naturalne mniejsze niż 1000, które przy dzieleniu przez 21 dają resztę 1. Spośród nich wybieramy te, które także przy dzieleniu przez 35 dają resztę 1. Takich liczb jest
(A) 8 (B) 9 (C) 10 (D) 11 (E) 12
14
[15] Janek porusza się na rowerze o 10 km /h szybciej niż Andrzej i przejechanie tego samego dystansu zajmuje mu jedną trzecią tego czasu, którego potrzebuje Andrzej. Prędkość Andrzeja wynosi
(A) 4 (B) 5 (C) 6 (D) 7 (E) 8
15
[16] Punkt M , będący środkiem kwadratu ABCD połączono z punktem P, leżącym na boku BC. Podaj długość odcinka BP, jeżeli wiadomo, że długość boku kwadratu wynosi 1 a pole trójkąta BMP jest 1/5 pola kwadratu ABCD.
16
[17] Anna mówi, że Barbara kłamie. Barbara mówi, że Cecylia kłamie. Cecylia mówi, że Barbara kłamie. Dorota mówi, że Anna kłamie. Ile dziewcząt kłamie ?
(E) 4 (D) 3 (C) 2 (B) 1 (A) 0 17
[18] Na rysunku przedstawiono okrąg wpisany w kwadrat i drugi mniejszy okrąg styczny zewnętrznie do dużego okręgu i dwóch boków kwadratu. Bok kwadratu ma długość 2. Jaka jest długość promienia mniejszego okręgu?
18
[19] Agnieszka jest abonentką sieci PLUS. Zwykle zostawia telefon włączony. Jeżeli telefon jest włączony, ale Agnieszka go nie używa, bateria wystarcza na 24 godziny. Jeżeli telefon jest stale w użyciu, bateria wystarcza na 3 godziny. Od ostatniego ładowania upłynęło 9 godzin a telefon był używany w tym czasie przez 60 minut. Jeżeli Agnieszka zostawi telefon włączony, ale nie będzie go używać, to na ile czasu jeszcze wystarczy bateria ?
(A) 7 (B) 8 (C) 11 (D) 14 (E) 15
19
[20] Długość boku kwadratu ABCD ma 3 jednostki. Odcinek PQ przechodzi przez środek kwadratu O i przecina bok AB w punkcie Q oddalonym od B o x jednostek. Pole zacieniowanej figury wynosi 20