NOTACJA WYKŁADNICZA Przy zapisywaniu bardzo dużych i

NOTACJA WYKŁADNICZA
Przy zapisywaniu bardzo dużych i bardzo małych liczb dodatnich, wygodnie jest posługiwać
się tzw. notacją wykładniczą. Polega ona na zapisywaniu liczb w postaci iloczynu, w którym
pierwszy czynnik jest liczbą większą od 1 i mniejszą od 10, a drugi jest potęgą liczby 10.
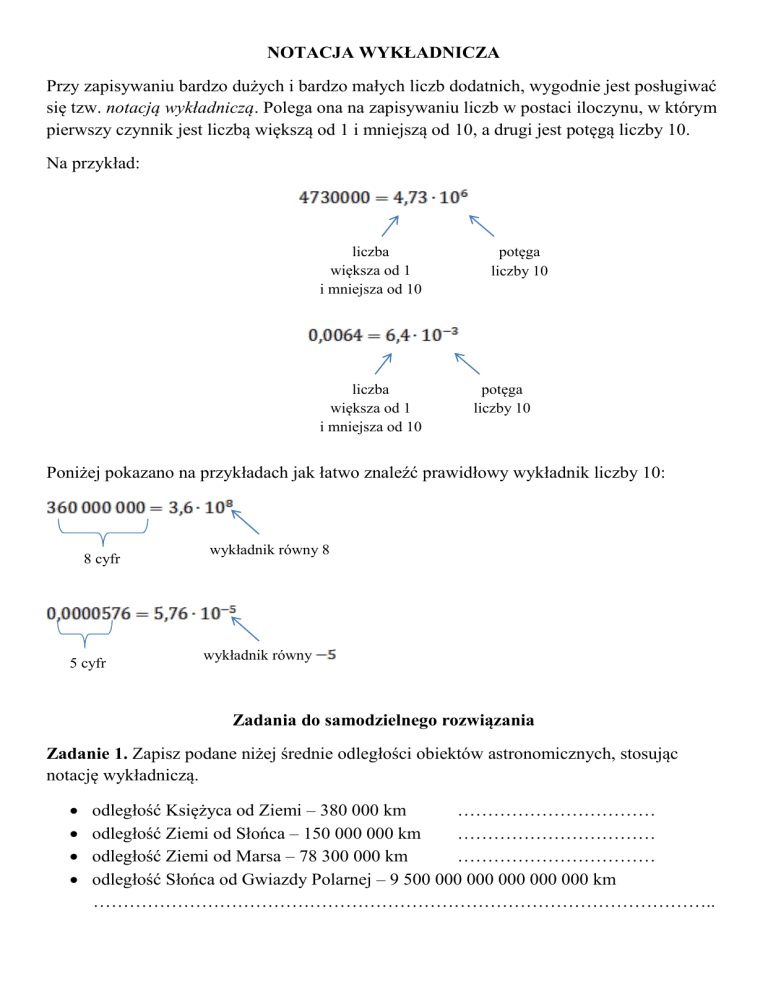
Na przykład:
liczba
większa od 1
i mniejsza od 10
liczba
większa od 1
i mniejsza od 10
potęga
liczby 10
potęga
liczby 10
Poniżej pokazano na przykładach jak łatwo znaleźć prawidłowy wykładnik liczby 10:
8 cyfr
5 cyfr
wykładnik równy 8
wykładnik równy
Zadania do samodzielnego rozwiązania
Zadanie 1. Zapisz podane niżej średnie odległości obiektów astronomicznych, stosując
notację wykładniczą.




odległość Księżyca od Ziemi – 380 000 km
……………………………
odległość Ziemi od Słońca – 150 000 000 km
……………………………
odległość Ziemi od Marsa – 78 300 000 km
……………………………
odległość Słońca od Gwiazdy Polarnej – 9 500 000 000 000 000 000 km
…………………………………………………………………………………………..
 odległość Słońca od Alfa Centauri – 40 200 000 000 000 000 km
…………………………………………………………………………………………..
Zadanie 2. Przedstaw podane wielkości w notacji wykładniczej:





średnica tułowia ameby – 0,00062 m
masa wirusa ospy – 0,000000000007 g
masa ziarenka maku – 0,0005 g
masa atomu wodoru – 0,00000000000000000000000167 g
prędkość z jaką rośnie bambus – 0,000012 m/s
……………………
……………………
……………………
……………………
……………………
Zadanie 3. Zapisz liczbę w postaci dziesiętnej.
Przykłady:
a)
b)
c)
d)
e)
f)
g)
h)
Zadania egzaminacyjne w latach ubiegłych:
Zadanie 1.
W różnych publikacjach jako jednostka energii pojawia się czasem toe.
1 toe odpowiada energii, jaką uzyskuje się z 1 tony ropy naftowej i równa się 41 868 MJ
(1 MJ = 1 000 000 J). Ilu dżulom równa się 1 toe?
11
8
9
10
A. 4,1868 · 10
B. 4,1868 · 10
C. 4,1868 · 10
D. 4,1868 · 10
Zadanie 2.
Średnia odległość Marsa od Słońca wynosi
km. Odległość ta zapisana bez
użycia potęgi jest równa
A. 22 800 000 km
B. 228 000 000 km
C. 2 280 000 000 km
D. 22 800 000 000 km