Podstawy Fizyki, Elektronika I rok

Fizyka Techniczna III semestr
(Zestaw 2)
1. Na podstawie pierwszej zasady termodynamiki wyprowadzić równanie opisujące adiabatę
dla gazu doskonałego. Napisać równanie adiabaty dla współrzędnych (p,V) , (p,T) oraz
(V,T).
2. Rozważyć n moli gazu doskonałego o znanym stosunku  = cp /cv. Napisać pierwszą
zasadę termodynamiki, a następnie wyliczyć ciepło pobrane przez gaz, pracę wykonaną
nad gazem i zmianę energii wewnętrznej gazu dla następujących przemian:
a) izochorycznej przy objętości V od ciśnienia p1 do p2,
b) izobarycznej przy ciśnieniu p od objętości V1 do V2 i wyznaczyć różnicę cp -cv,
c) izotermicznej przy temperaturze T od objętości V1 do V2,
d) adiabatycznej od objętości V1 do V2 , jeżeli ciśnienie początkowe wynosiło p1.
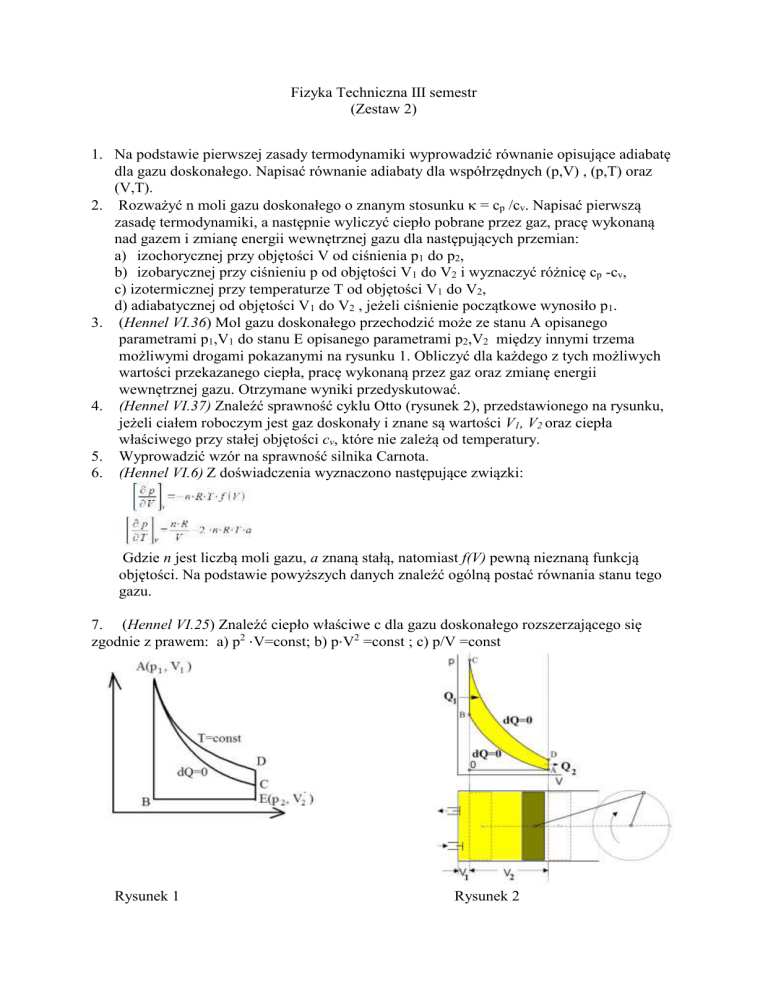
3. (Hennel VI.36) Mol gazu doskonałego przechodzić może ze stanu A opisanego
parametrami p1,V1 do stanu E opisanego parametrami p2,V2 między innymi trzema
możliwymi drogami pokazanymi na rysunku 1. Obliczyć dla każdego z tych możliwych
wartości przekazanego ciepła, pracę wykonaną przez gaz oraz zmianę energii
wewnętrznej gazu. Otrzymane wyniki przedyskutować.
4. (Hennel VI.37) Znaleźć sprawność cyklu Otto (rysunek 2), przedstawionego na rysunku,
jeżeli ciałem roboczym jest gaz doskonały i znane są wartości V1, V2 oraz ciepła
właściwego przy stałej objętości cv, które nie zależą od temperatury.
5. Wyprowadzić wzór na sprawność silnika Carnota.
6. (Hennel VI.6) Z doświadczenia wyznaczono następujące związki:
Gdzie n jest liczbą moli gazu, a znaną stałą, natomiast f(V) pewną nieznaną funkcją
objętości. Na podstawie powyższych danych znaleźć ogólną postać równania stanu tego
gazu.
7. (Hennel VI.25) Znaleźć ciepło właściwe c dla gazu doskonałego rozszerzającego się
zgodnie z prawem: a) p2 ⋅V=const; b) p⋅V2 =const ; c) p/V =const
Rysunek 1
Rysunek 2