wykaz, że

Poniżej zebrane zadania z oryginalnych arkuszy maturalnych CKE typu „wykaz, że”
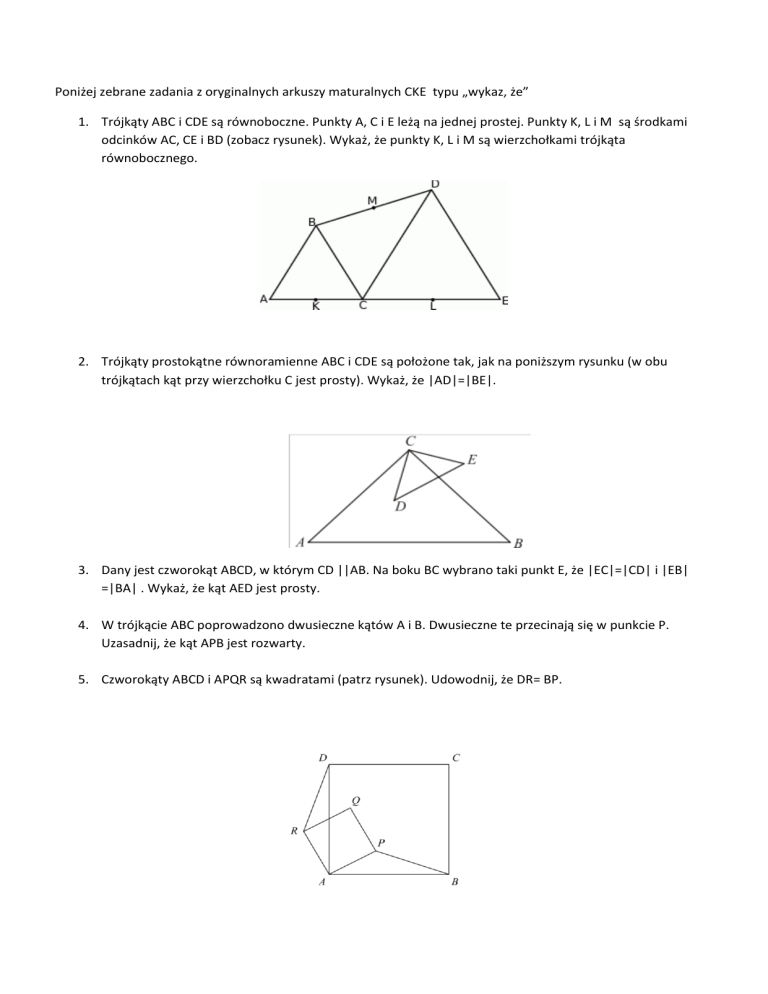
1. Trójkąty ABC i CDE są równoboczne. Punkty A, C i E leżą na jednej prostej. Punkty K, L i M są środkami
odcinków AC, CE i BD (zobacz rysunek). Wykaż, że punkty K, L i M są wierzchołkami trójkąta
równobocznego.
2. Trójkąty prostokątne równoramienne ABC i CDE są położone tak, jak na poniższym rysunku (w obu
trójkątach kąt przy wierzchołku C jest prosty). Wykaż, że |AD|=|BE|.
3. Dany jest czworokąt ABCD, w którym CD ||AB. Na boku BC wybrano taki punkt E, że |EC|=|CD| i |EB|
=|BA| . Wykaż, że kąt AED jest prosty.
4. W trójkącie ABC poprowadzono dwusieczne kątów A i B. Dwusieczne te przecinają się w punkcie P.
Uzasadnij, że kąt APB jest rozwarty.
5. Czworokąty ABCD i APQR są kwadratami (patrz rysunek). Udowodnij, że DR= BP.
6. Na boku BC trójkąta ABC wybrano punkt D tak, że kąt CAD=kąt ABC . Odcinek AE jest dwusieczną kąta
DAB. Udowodnij, że |CE| =|AC|.
7. Punkt E leży na ramieniu BC trapezu ABCD, w którym AB||CD. Udowodnij, że kątAED =kątBAE+kąt CDE.
8. Punkty D i E dzielą bok BC trójkąta ABC na trzy równe części (zobacz rysunek). Wykaż, że pole trójkąta ADE
jest trzy razy mniejsze od pola trójkąta ABC.
9. Na bokach trójkąta równobocznego ABC (na zewnątrz tego trójkąta) zbudowano kwadraty ABDE, CBGH
i ACKL. Udowodnij, że trójkąt KGE jest równoboczny.
10. Dany jest równoległobok ABCD. Na przedłużeniu przekątnej AC wybrano punkt E tak, że |CE|=0,5| AC|
(zobacz rysunek). Uzasadnij, że pole równoległoboku ABCD jest cztery razy większe od pola trójkąta DCE.
11. Trójkąt ABC przedstawiony na poniższym rysunku jest równoboczny, a punkty B, C, N są współliniowe. Na
boku AC wybrano punkt M tak, że |AM|=|CN| . Wykaż, że| BM| =|MN|.
12. Wykaż, że jeżeli ramiona AD i BC trapezu ABCD o podstawach AB i CD zawierają się w prostych
prostopadłych (zobacz rysunek), to
.
13. Wewnątrz kwadratu ABCD wybrano takie punkty M i N, że trójkąty ABM i BCN są równoboczne (zobacz
rysunek). Udowodnij, że trójkąt DNM jest równoboczny.
14. Dany jest prostokąt ABCD. Okręgi o średnicach AB i AD przecinają się w punktach A i P (zobacz rysunek).
Wykaż, że punkty B, P i D leżą na jednej prostej.