Symediany

Symediany
A
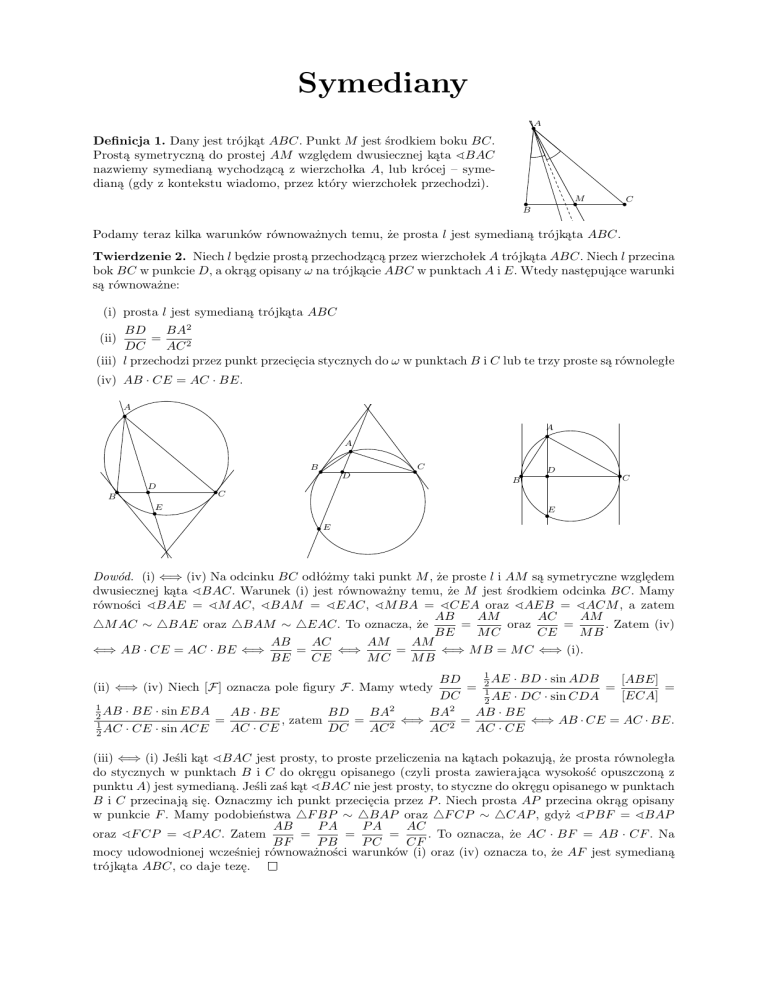
Definicja 1. Dany jest trójkąt ABC. Punkt M jest środkiem boku BC.
Prostą symetryczną do prostej AM względem dwusiecznej kąta ^BAC
nazwiemy symedianą wychodzącą z wierzchołka A, lub krócej – symedianą (gdy z kontekstu wiadomo, przez który wierzchołek przechodzi).
M
C
B
Podamy teraz kilka warunków równoważnych temu, że prosta l jest symedianą trójkąta ABC.
Twierdzenie 2. Niech l będzie prostą przechodzącą przez wierzchołek A trójkąta ABC. Niech l przecina
bok BC w punkcie D, a okrąg opisany ω na trójkącie ABC w punktach A i E. Wtedy następujące warunki
są równoważne:
(i) prosta l jest symedianą trójkąta ABC
BD
BA2
=
DC
AC 2
(iii) l przechodzi przez punkt przecięcia stycznych do ω w punktach B i C lub te trzy proste są równoległe
(ii)
(iv) AB · CE = AC · BE.
A
A
A
C
B
D
D
D
C
B
C
B
E
E
E
Dowód. (i) ⇐⇒ (iv) Na odcinku BC odłóżmy taki punkt M , że proste l i AM są symetryczne względem
dwusiecznej kąta ^BAC. Warunek (i) jest równoważny temu, że M jest środkiem odcinka BC. Mamy
równości ^BAE = ^M AC, ^BAM = ^EAC, ^M BA = ^CEA oraz ^AEB = ^ACM , a zatem
AB
AM
AC
AM
4M AC ∼ 4BAE oraz 4BAM ∼ 4EAC. To oznacza, że
=
oraz
=
. Zatem (iv)
BE
MC
CE
MB
AB
AC
AM
AM
⇐⇒ AB · CE = AC · BE ⇐⇒
=
⇐⇒
=
⇐⇒ M B = M C ⇐⇒ (i).
BE
CE
MC
MB
1
AE · BD · sin ADB
[ABE]
BD
= 21
=
=
DC
[ECA]
2 AE · DC · sin CDA
1
AB · BE
BD
BA2
BA2
AB · BE
2 AB · BE · sin EBA
=
,
zatem
=
⇐⇒ AB · CE = AC · BE.
⇐⇒
=
1
2
2
AC
·
CE
DC
AC
AC
AC · CE
2 AC · CE · sin ACE
(ii) ⇐⇒ (iv) Niech [F] oznacza pole figury F. Mamy wtedy
(iii) ⇐⇒ (i) Jeśli kąt ^BAC jest prosty, to proste przeliczenia na kątach pokazują, że prosta równoległa
do stycznych w punktach B i C do okręgu opisanego (czyli prosta zawierająca wysokość opuszczoną z
punktu A) jest symedianą. Jeśli zaś kąt ^BAC nie jest prosty, to styczne do okręgu opisanego w punktach
B i C przecinają się. Oznaczmy ich punkt przecięcia przez P . Niech prosta AP przecina okrąg opisany
w punkcie F . Mamy podobieństwa 4F BP ∼ 4BAP oraz 4F CP ∼ 4CAP , gdyż ^P BF = ^BAP
AB
PA
PA
AC
oraz ^F CP = ^P AC. Zatem
=
=
=
. To oznacza, że AC · BF = AB · CF . Na
BF
PB
PC
CF
mocy udowodnionej wcześniej równoważności warunków (i) oraz (iv) oznacza to, że AF jest symedianą
trójkąta ABC, co daje tezę.
Zadanie 3. Dany jest trójkąt ABC oraz punkty D i E na prostych AB i AC takie, że kąt ^EDA ma
taką samą miarę jak kąt ^ACB. Wykaż, że symediana trójkąta ABC poprowadzona z wierzchołka A
przechodzi przez środek odcinka DE.
Rozwiązanie. Niech M oraz N będą środkami odcinków BC oraz DE. Wystarczy pokazać, że AN jest symedianą trójkąta ABC. Trójkąty ABC oraz ADE
BC
ED
=
. Korzystając z faktu, że
są podobne (mają równe kąty), zatem
DA
CA
ND
MC
2N D = ED oraz 2M C = BC, dostajemy
=
, co wraz z równością
DA
CA
kątów ^EDA oraz ^ACB oznacza, że trójkąty N DA oraz M CA są podobne (bkb). Stąd ^DAN = ^M AC. Ta równość oznacza, że proste AM i AN
są symetryczne względem dwusiecznej kąta ^BAC. Skoro AM jest środkową
trójkąta ABC, to AN jest jego symedianą.
A
E
N
D
M
C
B
Zadanie 4. Dany jest trójkąt ABC. Symediana tego trójkąta wychodząca z wierzchołka A przecina
okrąg opisany w punkcie D. Punkt M jest środkiem odcinka AD. Wykaż, że kąty ^BM D, ^DM C oraz
^BAC mają równe miary.
A
Rozwiązanie. Ponieważ AD jest symedianą, więc AB·CD = AC·BD. To
oznacza, że BC jest symedianą trójkąta ABD. Zatem ^DBM = ^CBA.
Ponadto ^M DB = ^ACB. Stąd wynika, że 4ABC ∼ 4M BD (na mocy cechy kąt-kąt-kąt), zatem ^BM D = ^BAC. Podobnie pokazujemy,
że ^DM C = ^BAC.
M
C
B
D
Zadanie 5. Wykaż, że jeśli punkt X leży na symedianie trójkąta ABC poprowadzonej z wierzchołka A,
to iloraz odległości punktu X od prostych AB i AC jest równy ilorazowi długości boków AB i AC. Czy
każdy punkt mający tę własność leży na symedianie trójkąta ABC?
Rozwiązanie. Obierzmy dowolny punkt X na tej symedianie. Przeprowadźmy go jednokładnością o środku w punkcie A na punkt D leżący
na okręgu opisanym na trójkącie ABC. Iloraz odległości punktu X od
prostych AB i AC jest taki sam jak iloraz odległości punktu D od tych
prostych (bo każda z odległości przemnoży się przez wartość bezwzględną skali podobieństwa). Niech E oraz F będą rzutami prostokątnymi
punktu D na proste AB i AC. Trójkąty prostokątne DEB i DF C mają
DE
DB
=
, a ostatni ułamek, w
równe kąty, więc są podobne, zatem
DF
DC
AB
myśl równości AB · CD = DB · AC, równa się
.
AC
W powyższym rozwiązaniu przeprowadzaliśmy punkt X jednokładnością
o środku w punkcie A i niezerowej skali na punkt leżący na okręgu opisanym. Okazuje się, że punkty, dla których nie istnieje taka jednokładność
(czyli punkty leżące na stycznej w punkcie A do okręgu opisanego) też
spełniają warunek dany w zadaniu, co pozostawiamy jako ćwiczenie dla
Czytelnika.
X2
X3
A
X1
F
C
B
E
D
Zadanie 6. Wykaż, że symediany trójkąta przecinają się w jednym punkcie. Punkt ten nazywany jest
punktem Lemoine’a.
Rozwiązanie. Niech symediany trójkąta ABC przecinają boki BC, CA i AB w punktach D, E oraz F .
BD
BA2 CE
CB 2
AF
AC 2
Wówczas
=
,
=
oraz
=
. Po pomnożeniu tych równości stronami otrzyDC
AC 2 EA
BA2
FB
CB 2
BD CE AF
·
·
= 1, co na mocy twierdzenia Cevy daje tezę.
mujemy
DC EA F B
Zadanie 7. Na półprostych AB i AC obrano punkty C 0 i B 0 tak, że AC 0 = AC oraz AB = AB 0 .
Wykaż, że środek odcinka B 0 C 0 leży na symedianie trójkąta ABC.
Wskazówka. Skorzystaj z zadania 3.
Zadanie 8. Na zewnątrz trójkąta ABC zbudowano kwadraty ABDE oraz ACF G. Wykaż, że punkt
przecięcia prostych DE oraz F G leży na symedianie trójkąta ABC.
Wskazówka. Skorzystaj z zadania 5.
Zadanie 9. W czworokącie ABCD punkt M jest środkiem przekątnej AC. Wykaż, że jeśli ^DM A =
^AM B = ^DCB, to na czworokącie ABCD można opisać okrąg.
Wskazówka. Skorzystaj z zadania 4.
Zadanie 10. Punkt M jest środkiem boku BC trójkąta ostrokątnego ABC. Punkt K leży na boku
BC i spełnia warunek ^BAM = ^KAC. Na odcinku AK wybrano taki punkt E, że ^BEK = ^BAC.
Pokaż, że ^KEC = ^BAC.
Wskazówka. Skorzystaj z zadania 4.
Zadanie 11. Dany jest trójkąt ABC, w którym AC = BC. Punkt P leży wewnątrz trójkąta ABC,
przy czym ^P AB = ^P BC. Punkt M jest środkiem boku AB. Pokaż, że ^AP M + ^BP C = 180◦ .
Wskazówka. Zauważ, że okrąg opisany na trójkącie P AB jest styczny do prostych CA i CB.
Zadanie 12. Dany jest okrąg o i jego cięciwa AB niebędąca średnicą. Na okręgu o wybieramy punkt P ,
różny od punktów A i B. Punkty Q i R leżą odpowiednio na prostych AP i BP , przy czym QP = QB
oraz RP = RA. Punkt M jest środkiem odcinka QR. Wykaż, że wszystkie uzyskane w ten sposób proste
P M (odpowiadające różnym położeniom punktu P na okręgu o) mają punkt wspólny.
Wskazówka. Skorzystaj z zadania 3.
Zadanie 13. Niech L będzie punktem Lemoine’a trójkąta ABC. Punkty P i Q leżą na prostej BC,
punkty R i S na prostej CA, a punkty T i U na prostej AB, przy czym RU k BC, QT k CA, SP k AB
oraz odcinki RU , QT i SP przecinają się w punkcie L. Wykaż, że punkty P , Q, R, S, T i U leżą na
jednym okręgu. Okrąg ten nazywany jest pierwszym okręgiem Lemoine’a.
Wskazówka. Skorzystaj z zadania 3.
Zadanie 14. Niech L będzie punktem Lemoine’a trójkąta ABC. Przez punkt L poprowadzono prostą
przecinającą odcinki BC i CA w punktach P i Q, przy czym ^P QC = ^CBA. Przez punkt L poprowadzono też prostą przecinającą odcinki BC i AB w punktach R i S, przy czym ^BSR = ^ACB. Wykaż,
że czworokąt P RQS jest prostokątem.
Wskazówka. Skorzystaj z zadania 3.
Zadanie 15. Niech L będzie punktem Lemoine’a trójkąta ABC. Punkty P i Q leżą na prostej BC,
punkty R i S na prostej CA, a punkty T i U na prostej AB, przy czym ^RU A = ^ACB, ^T QB =
^BAC, ^P SC = ^CBA oraz odcinki RU , QT i SP przecinają się w punkcie L. Wykaż, że punkty P ,
Q, R, S, T i U leżą na jednym okręgu. Okrąg ten nazywany jest drugim okręgiem Lemoine’a.
Wskazówka. Skorzystaj z zadania 14.
Zadanie 16. Niech AD będzie wysokością trójkąta ABC. Niech M i N będą środkami odcinków BC i
AD. Wykaż, że punkt Lemoine’a trójkąta ABC leży na prostej M N .
Wskazówka. Skorzystaj z zadania 14.
Zadanie 17. Dany jest trójkąt ABC, w którym AB 6= AC. Okrąg o wpisany w ten trójkąt jest styczny
do boków BC, CA i AB w punktach D, E i F . Punkt M jest środkiem odcinka EF . Okrąg o średnicy
M D przecina okrąg o w punktach D i P oraz przecina odcinek EF w punktach M i Q. Wykaż, że prosta
P Q połowi odcinek AM .
Wskazówka. Pokaż, że proste P M i DQ przecinają się w ortocentrum trójkąta DEF , a prosta AP przez
odbicie tego ortocentrum względem prostej EF .
Zadanie 18. Dany jest trójkąt ABC. Styczne w punktach B i C do okręgu opisanego przecinają się
w punkcie P . Punkty Q i R są rzutami punktu P na proste AB i AC. Wykaż, że prosta zawierająca
wysokość trójkąta AQR opuszczoną z punktu A przechodzi przez środek odcinka BC.
Zadanie 19. Dany jest czworokąt ABCD wpisany w okrąg ω. Wykaż równoważność następujących
warunków:
(i) AB · CD = BC · DA
(ii) BD jest symedianą trójkąta ABC
(iii) BD jest symedianą trójkąta CDA
(iv) AC jest symedianą trójkąta DAB
(v) AC jest symedianą trójkąta BCD
(vi) styczne do ω w punktach A i C oraz prosta BD są współpękowe lub równoległe
(vii) styczne do ω w punktach B i D oraz prosta AC są współpękowe lub równoległe
Uwaga. Czworokąty spełniające powyższe własności są nazywane czworokątami harmonicznymi. Więcej
własności czworokątów harmonicznych można znaleźć w literaturze.
Zadanie 20. Niech punkty P i Q leżą na bokach AB i AC trójkąta ABC, przy czym proste BQ i
CP są symedianami trójkąta ABC. Niech punkty R i S będą środkami odcinków BQ i CP . Wykaż, że
^CBS = ^RCB.
Zadanie 21. Czworokąt ABCD jest wpisany w okrąg. Niech P , Q i R będą rzutami punktu D na proste
BC, CA i AB odpowiednio. Wykaż, że jeśli P Q = QR wtedy i tylko wtedy, gdy dwusieczne kątów ABC
i ADC przecinają się na prostej AC.
Zadanie 22. Niech L będzie punktem Lemoine’a trójkąta ABC i niech proste AL, BL i CL przecinają
okrąg opisany na trójkącie ABC po raz drugi w punktach D, E i F . Wykaż, że punkt L jest punktem
Lemoine’a trójkąta DEF .
opracował: Tomasz Cieśla