2 Figury geometryczne

Płaszczyzna, proste...
2
Figury geometryczne
1 Płaszczyzna, proste i półproste
n
o
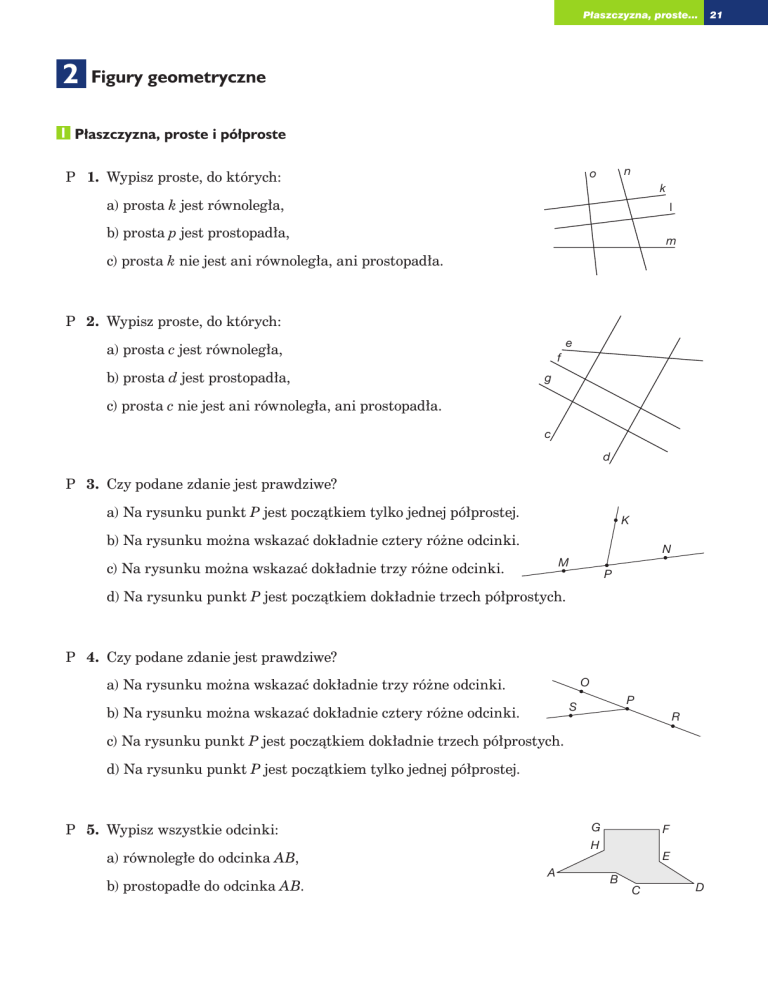
P 1. Wypisz proste, do których:
k
a) prosta k jest równoległa,
l
b) prosta p jest prostopadła,
m
c) prosta k nie jest ani równoległa, ani prostopadła.
P 2. Wypisz proste, do których:
e
a) prosta c jest równoległa,
b) prosta d jest prostopadła,
f
g
c) prosta c nie jest ani równoległa, ani prostopadła.
c
d
P 3. Czy podane zdanie jest prawdziwe?
a) Na rysunku punkt P jest początkiem tylko jednej półprostej.
K
b) Na rysunku można wskazać dokładnie cztery różne odcinki.
N
M
c) Na rysunku można wskazać dokładnie trzy różne odcinki.
P
d) Na rysunku punkt P jest początkiem dokładnie trzech półprostych.
P 4. Czy podane zdanie jest prawdziwe?
O
a) Na rysunku można wskazać dokładnie trzy różne odcinki.
P
S
b) Na rysunku można wskazać dokładnie cztery różne odcinki.
R
c) Na rysunku punkt P jest początkiem dokładnie trzech półprostych.
d) Na rysunku punkt P jest początkiem tylko jednej półprostej.
P 5. Wypisz wszystkie odcinki:
a) równoległe do odcinka AB, b) prostopadłe do odcinka AB.
G
F
H
A
E
B
C
D
21
22
Figury geometryczne
P 6. Wypisz wszystkie odcinki:
F
A
a) równoległe do odcinka AB,
H
b) prostopadłe do odcinka AB.
D
G
B
P 7. Dane są punkty A, B i C. Narysuj:
E
C
A
a) półprostą o początku B, do której nie należy punkt A,
B
C
b) półprostą o początku C, do której należy punkt B,
c) odcinek AC.
P 8. Dane są punkty A, B i C. Narysuj:
A
B
a) półprostą o początku A, do której nie należy punkt C,
C
b) półprostą o początku B, do której należy punkt C,
c) odcinek AB.
PP 9. Dane są punkty A i B oraz prosta k. Narysuj:
A
a) prostą równoległą do prostej k, przechodzącą przez punkt A,
b) prostą prostopadłą do prostej k, przechodzącą przez punkt B.
k
B
PP 10. Dane są punkty A i B oraz prosta m. Narysuj:
a) prostą równoległą do prostej m, przechodzącą przez punkt B,
m
A
b) prostą prostopadłą do prostej m, przechodzącą przez punkt A.
B
2 Kąty. Rodzaje kątów
P 1. Określ rodzaj kąta o wierzchołku w punkcie:
F
E
a) A, b) D, c) E.
G
H
C
A
B
D
Kąty. Rodzaje kątów
P 2. Określ rodzaj kąta o wierzchołku w punkcie:
F
E
a) B, b) F, G
c) G.
P 3. Rysunek przedstawia plan dróg rozchodzących się
w lesie. Uzupełnij zdanie, wpisując odpowiedni rodzaj
kąta wypukłego.
a) Drogi „do wsi” i „do polany” tworzą kąt
.
b) Drogi „do rzeki” i „do szosy” tworzą kąt
.
c) Drogi „do polany” i „do cegielni” tworzą kąt
.
H
C
A
B
do cegielni
D
do wsi
do polany
do rzeki
do szosy
P 4. Rysunek przedstawia plan dróg rozchodzących się
w lesie. Uzupełnij zdanie, wpisując odpowiedni rodzaj
kąta wypukłego.
a) Drogi „do cegielni” i „do szosy” tworzą kąt
.
b) Drogi „do szosy” i „do polany” tworzą kąt
.
c) Drogi „do wsi” i „do cegielni” tworzą kąt
.
do cegielni
do wsi
do polany
do rzeki
do szosy
P 5. Do półprostej o początku K dorysuj drugą półprostą o tym samym początku tak, aby powstał kąt danego rodzaju. Zaznacz ten kąt łukiem.
a) kąt ostry
b) kąt rozwarty
c) kąt prosty
K
K
K
P 6. Do półprostej o początku K dorysuj drugą półprostą o tym samym początku tak, aby powstał kąt danego rodzaju. Zaznacz ten kąt łukiem.
a) kąt półpełny
b) kąt ostry
K
c) kąt rozwarty
K
K
23
24
Figury geometryczne
P 7. Zaznacz łukami kąty ostre i kąty rozwarte.
a) Ile jest kątów ostrych?
b) Ile jest kątów rozwartych?
P 8. Zaznacz łukami kąty proste i kąty rozwarte.
a) Ile jest kątów prostych?
b) Ile jest kątów rozwartych?
PP 9. Na tarczy zegara dorysuj wskazówki i określ rodzaj mniejszego z kątów, które one tworzą
o godzinie:
a) 9.00,
b) 17.50,
11 12 1
10
9
11 12 1
2
10
3
9
4
8
7
6
c) 3.20.
9
4
7
kąt
10
3
8
5
11 12 1
2
6
3
4
8
5
7
kąt
2
6
5
kąt
PP 10. Na tarczy zegara dorysuj wskazówki i określ rodzaj mniejszego z kątów, które one tworzą
o godzinie:
a) 16.00,
b) 10.45, 11 12 1
10
9
10
9
4
8
7
kąt
11 12 1
2
3
6
c) 15.00.
3
10
9
4
8
5
11 12 1
2
7
6
kąt
PP 11. Jakiego rodzaju kąt zakreśli:
a) wskazówka minutowa w czasie 20 minut,
b) wskazówka godzinowa w czasie 2 godzin?
PP 12. Jakiego rodzaju kąt zakreśli:
a) wskazówka minutowa w czasie 10 minut,
b) wskazówka godzinowa w czasie 5 godzin?
3
4
8
5
7
kąt
2
6
5
Mierzenie kątów
3 Mierzenie kątów
P 1. Dobierz miary podane w ramce do odpowiednich kątów zaznaczonych na rysunku.
δ
ε
γ
a=
b=
90° 335° 20° 140° 70°
g=
β
d=
α
e=
P 2. Dobierz miary podane w ramce do odpowiednich kątów
zaznaczonych na rysunku.
ε
δ
a=
b=
90° 40° 336° 70° 120°
g=
γ
d=
α
e=
β
P 3. Oblicz brakującą miarę kąta.
a) b)
60 °
30 °
P 4. Oblicz brakującą miarę kąta.
a) b)
45 °
30 °
P 5. Określ rodzaj kąta o podanej mierze.
a) 90°
b) 39°
c) 98°
P 6. Określ rodzaj kąta o podanej mierze.
a) 102°
b) 21°
c) 180°
25
26
Figury geometryczne
PP 7. Oblicz miary kątów oznaczonych literami greckimi.
δ
γ
20 °
β
PP 8. Oblicz miary kątów oznaczonych literami greckimi.
50°
γ
α
β
4 Rodzaje i własności trójkątów
P 1. Czy z trzech odcinków o podanych długościach można zbudować trójkąt? Zapisz obliczenia
uzasadniające twoją odpowiedź.
a) 7 cm, 4 cm, 10 cm b) 6 cm, 8 cm, 15 cm
P 2. Czy z trzech odcinków o podanych długościach można zbudować trójkąt? Zapisz obliczenia
uzasadniające twoją odpowiedź.
a) 8 cm, 3 cm, 12 cm b) 6 cm, 5 cm, 10 cm
P 3. Podaj nazwy wszystkich trójkątów, które można wskazać
na rysunku. Określ rodzaj każdego z nich.
D
F
E
C
B
A
P 4. Podaj nazwy wszystkich trójkątów, które można wskazać
na rysunku. Określ rodzaj każdego z nich.
C
D
E
A
B
Własności trójkątów
β
δ
γ 110°
γ
P 5. Oblicz kąty oznaczone literami greckimi.
b) 40°
a) 40°
α
γ
δ
40°
40°
70°
γ 110°
β
P 6. Oblicz kąty oznaczone literami greckimi.
70°
a) c)
γ 110°
β
140°
120°
α
c)
140°
α
70°
b) α
γ
70°
β
α
110°
120°
70°
α
β
α
70°
α
α
PP 7. Oblicz kąty oznaczone literami greckimi.
110°
140°
a) α °
60° 12060°
γ
α
γ
α
α
α
β
β
α
β
40°
110°
α
b)
α
α
β
β
γ
γ
30°
40°
30°
α
PP 8. Oblicz kąty oznaczone literami greckimi.
a) b)
60°
60°
α
α
80°
β
γ
γ
β
β
γ
20°
γ
α
80°
β
α
20°
5 Własności niektórych trójkątów
P 1. Jaką długość mogą mieć boki trójkąta równoramiennego, jeśli jego obwód wynosi 12 cm?
A. 6 cm, 3 cm, 3 cm
C. po 12 cm
B. po 4 cm
D. 3 cm, 4 cm, 5 cm
27
28
Figury geometryczne
P 2. Jaką długość mogą mieć boki trójkąta równoramiennego, jeśli jego obwód wynosi 15 cm?
A. po 15 cm C. po 5 cm
B. 3 cm, 3 cm, 9 cm
D. 5 cm, 6 cm, 4 cm
P 3. W trójkącie równoramiennym podstawa ma długość 6 cm, a obwód jest równy 16 cm. Oblicz
długość ramienia tego trójkąta.
P 4. Obwód trójkąta równoramiennego wynosi 20 cm, a ramiona mają po 6 cm. Oblicz długość
podstawy tego trójkąta.
P 5. Uzupełnij zdania. Pamiętaj o podaniu dwóch określeń trójkąta (np. równoramienny ostrokątny).
a) Jeśli w prostokącie, który nie jest kwadratem, poprowadzimy dwie przekątne, to powstaną dwa trójkąty
i dwa trójkąty
.
b) Przekątne kwadratu ­­dzielą kwadrat na cztery trójkąty
.
P 6. Uzupełnij zdania. Pamiętaj o podaniu dwóch określeń trójkąta (np. równoramienny ostrokątny).
a) Jeśli w kwadracie poprowadzimy dwie przekątne, to powstaną cztery trójkąty
.
b) Przekątne prostokąta, który nie jest kwadratem, dzielą ten prostokąt na cztery trójkąty: dwa trójkąty
i dwa trójkąty
.
P 7. W trójkącie równoramiennym ramię jest o 2 cm dłuższe od podstawy, która ma 6 cm. Oblicz
obwód tego trójkąta.
P 8. W trójkącie równoramiennym podstawa ma 8 cm i jest o 2 cm krótsza od ramienia. Oblicz
obwód tego trójkąta.
PP 9. Jeden bok trójkąta jest o 2 cm krótszy od drugiego boku i o 3 cm krótszy od trzeciego.
Obwód tego trójkąta jest równy 17 cm. Wyznacz długości wszystkich jego boków.
PP 10. Jeden bok trójkąta jest o 1 cm krótszy od drugiego boku i o 3 cm krótszy od trzeciego.
Obwód tego trójkąta jest równy 19 cm. Wyznacz długości wszystkich jego boków.
PP 11. Dwa boki trójkąta mają długości 10 cm i 30 cm. Jaką długość może mieć trzeci bok?
A. 40 cm
B. 50 cm
C. 10 cm
D. 35 cm
Własności trójkątów
PP 12. Dwa boki trójkąta mają długości 20 cm i 50 cm. Jaką długość może mieć trzeci bok?
A. 80 cm
B. 70 cm
C. 60 cm
D. 20 cm
PP 13. Które z trójkątów są:
C
a) równoramienne ostrokątne,
b) różnoboczne,
A
c) prostokątne?
B
D
F
E
PP 14. Które z trójkątów są:
B
a) równoramienne ostrokątne,
C
b) równoboczne,
A
c) prostokątne?
E
D
F
PP 15. W trójkącie równoramiennym podstawa jest o 2 cm krótsza od ramienia. Obwód tego trójkąta wynosi 16 cm. Oblicz długości jego boków.
PP 16. W trójkącie równoramiennym ramię jest o 3 cm dłuższe od podstawy. Obwód tego trójkąta
wynosi 18 cm. Oblicz długości jego boków.
29
30
Figury geometryczne
6 Wysokość trójkąta
K
P 1. Wypisz z rysunku wszystkie wysokości trójkąta SOK oraz boki, na
które te wysokości są opuszczone.
B
D
C
O
A
S
O
P 2. Wypisz z rysunku wszystkie wysokości trójkąta KOS oraz
boki, na które te wysokości są opuszczone.
A
S
C
D
B
K
P 3. Narysuj jedną wysokość trójkąta ABC.
a)
b)
C
c)
C
C
A
B
A
B
A
B
P 4. Narysuj jedną wysokość trójkąta ABC.
a)
b)
c)
C
C
C
A
B
A
B
A
B
Równoległoboki
PP 5. Odcinek CD jest wysokością trójkąta ABC. Oblicz kąty trójkątów ADC i BDC.
a)b)
B
B
D
D
C
20°
A
AD
C
10°
20°
10°
B
D
30°
B
A
30°
A
C
C
PP 6. Odcinek CD jest wysokością trójkąta ABC. Oblicz kąty trójkątów ADC i BCD.
a)b)
B
20°A
20°
D
D
C
C
A
B
30°
D B
30°
D
B
C
C
40°
40°
A
A
PP 7. Narysuj trójkąt równoramienny KLM, wiedząc, że wysokość poprowadzona z wierzchołka
M ma 4 cm i jest prostopadła do podstawy, a kąt między tą wysokością a ramieniem ma 25°.
Podaj miary kątów trójkąta KLM.
PP 8. Narysuj trójkąt równoramienny PRS, wiedząc, że wysokość poprowadzona z wierzchołka S
ma 5 cm i jest prostopadła do podstawy, a kąt między tą wysokością a ramieniem ma 35°.
Podaj miary kątów trójkąta PRS.
7 Równoległoboki
P 1. Nazwij figurę przedstawioną na rysunku oraz wypisz:
a) boki równoległe,
D
C
b) boki tej samej długości,
c) przekątne.
A
B
P 2. Nazwij figurę przedstawioną na rysunku oraz wypisz:
a) boki równoległe,
H
G
b) boki tej samej długości,
c) przekątne.
E
F
31
32
Figury geometryczne
P 3. Czy podane zdanie jest prawdziwe?
a) Każda przekątna równoległoboku dzieli go na dwa identyczne trójkąty.
b) Przekątne rombu, który nie jest kwadratem, są tej samej długości.
c) Przekątne rombu dzielą go na cztery identyczne trójkąty.
d) W każdym równoległoboku przekątne są tej samej długości.
P 4. Czy podane zdanie jest prawdziwe?
a) Przekątne równoległoboku, który nie jest rombem, dzielą go na cztery identyczne trójkąty.
b) W każdym równoległoboku punkt przecięcia przekątnych dzieli każdą z nich na połowy.
c) W każdym równoległoboku wszystkie kąty mają taką samą miarę.
d) Przekątne rombu przecinają się pod kątem prostym.
P 5. Ile jest równy obwód równoległoboku, którego jeden bok ma 8 cm, a drugi jest o 2 cm krótszy?
A. 32 cm
B. 24 cm
C. 14 cm
D. 28 cm
P 6. Ile jest równy obwód równoległoboku, którego jeden bok ma 6 cm, a drugi jest o 3 cm dłuższy?
A. 18 cm
B. 30 cm
C. 36 cm
D. 15 cm
P 7. Oblicz miary kątów równoległoboku oznaczone literami greckimi.
a)
b)
δ
108°
γ
δ
β
34°
β
γ
P 8. Oblicz miary kątów równoległoboku oznaczone literami greckimi.
γ
γ
a)b)
53°
53°
β
β
β
β
δ
δ
131°
δ
131°
γ
δ
γ
PP 9. Oblicz miary kątów równoległoboku oznaczone literami greckimi.
a)b)
γ
γ
δ
δ
δ
δ
108° α
108° α
β
αβ
α
β
γ
β
44°
γ
44°
Wysokość równoległoboku
γ
δ
PP 10. Oblicz miary kątów równoległoboku oznaczone literami greckimi.
a)b)
γ
δ
α
α
β 76°
α
δ
γ
γ
β
155°
β
155°
α
β 76°
δ
PP 11. Obwód równoległoboku wynosi 30 cm, a jego dłuższy bok ma 11 cm. Oblicz długości pozostałych boków.
PP 12. Obwód równoległoboku wynosi 30 cm, a jego krótszy bok ma 6 cm. Oblicz długości pozostałych boków.
8 Wysokość równoległoboku
P 1. Wypisz odcinki, które są wysokościami równoległoboku KLMN.
M
N
Z
L
K
Y
X
P 2. Wypisz odcinki, które są wysokościami równoległoboku KLMN.
N
K
X
Y
M
Z
L
33
34
Figury geometryczne
P 3. Narysuj wysokości równoległoboku przedstawionego na rysunku.
P 4. Narysuj wysokości równoległoboku przedstawionego na rysunku.
PP 5. Dokończ rysunek równoległoboku ABCD, wiedząc, że odcinki DP i DR są jego wysokościami.
D
R
A
P
PP 6. Dokończ rysunek równoległoboku ABCD, wiedząc, że odcinki BR i BP są jego wysokościami.
P
C
R
B
PP 7. Narysuj równoległobok PRST o bokach 4 cm i 7 cm oraz kącie ostrym 60°. Narysuj jego
wysokości.
PP 8. Narysuj równoległobok ABCD o bokach 5 cm i 8 cm oraz kącie ostrym 50°. Narysuj jego
wysokości.
Trapezy
9 Trapezy
P 1. Wypisz trapezy, które można wskazać na rysunku. Które z nich to trapezy równoramienne,
a które – prostokątne?
e
a
d
c
b
P 2. Wypisz trapezy, które można wskazać na rysunku. Które z nich to trapezy równoramienne,
a które – prostokątne?
p
m
o
n
k
P 3. Odcinek EK jest wysokością trapezu, którego podstawy mają długości 4 kratki i 2 kratki.
Dorysuj odpowiednie odcinki tak, aby powstał:
a) trapez równoramienny, b) trapez prostokątny.
K
K
E
E
P 4. Odcinek EK jest wysokością trapezu, którego podstawy mają długości 6 kratek i 4 kratki.
Dorysuj odpowiednie odcinki tak, aby powstał:
a) trapez równoramienny, b) trapez prostokątny.
K
K
E
E
35
36
Figury geometryczne
P 5. Oblicz miary kątów trapezu oznaczone literami greckimi.
a)
b)
110°
c)
120°
130°
γ
β
γ
β
α
δ
40°
α
40°
P 6. Oblicz miary kątów trapezu oznaczone literami greckimi.
a)
b)
α
αβ
β
c)
δ
110° 110° 110° 110°
α
60° 60°
40° 40°
γ
γ
δ
δ
δ
α
β
β
30° 30°
PP 7. Oblicz obwód trapezu.
a)b)
2 cm
2 cm
4 cm
4 cm
3 cm
3 cm
5 cm
4 cm 5 cm
4 cm
4 cm
4 cm
1 cm
1 cm
1 cm
1 cm
3 cm
3 cm
PP 8. Oblicz obwód trapezu.
a)b)
3 cm
3 cm
5 cm
5 cm
2 cm
4 cm
4 cm
2 cm
1 cm
4 cm
4 cm
1 cm
2 cm
2 cm
1 cm
5 cm
5 cm
1 cm
Klasyfikacja czworokątów
­­­ 10 Klasyfikacja czworokątów
P 1. Wielokąt ABCDEF jest sześciokątem, którego wszystkie boki
mają taką samą długość, a wszystkie kąty taką samą miarę.
Wpisz w puste miejsce, jakim czworokątem jest wskazana figura. Skorzystaj z odpowiednich przyrządów geometrycznych.
a) Czworokąt FCDE jest
.
b) Czworokąt ABCG jest
.
c) Czworokąt FHDE jest
.
E
F
P 2. Wielokąt ABCDEF jest sześciokątem, którego wszystkie boki
mają taką samą długość, a wszystkie kąty taką samą miarę.
Wpisz w puste miejsce, jakim czworokątem jest wskazana figura. Skorzystaj z odpowiednich przyrządów geometrycznych.
a) Czworokąt GCDE jest
.
b) Czworokąt ABCF jest
.
c) Czworokąt BCDH jest
.
F
G
D
H
C
A
B
E
D
G
H
C
A
B
P 3. Czy podane zdanie jest prawdziwe?
a) Jeśli czworokąt ma jedną parę boków równoległych, to jest trapezem.
b) Czworokąt, w którym wszystkie kąty mają równe miary, jest kwadratem.
c) Każdy kwadrat jest równoległobokiem.
d) W trapezie suma miar kątów przy każdym boku wynosi 180°.
P 4. Czy podane zdanie jest prawdziwe?
a) Jeśli w czworokącie trzy kąty mają po 90°, to ten czworokąt jest prostokątem.
b) Czworokąt o wszystkich bokach tej samej długości jest kwadratem.
c) Każdy równoległobok jest prostokątem.
d) W równoległoboku suma miar kątów przy każdym boku wynosi 180°.
PP 5. Oblicz miary kątów czworokąta oznaczone
literami greckimi.
105° α
δ
120°
β
50°
37
38
Figury geometryczne
PP 6. Oblicz miary kątów czworokąta oznaczone literami greckimi.
60°
β
γ
40°
α
95°
11 Zadania dodatkowe
 1. W równoległoboku kąt ostry jest o 110° mniejszy od kąta rozwartego. Podaj miary kątów
tego równoległoboku.
 2. W równoległoboku kąt rozwarty jest o 50° większy od kąta ostrego. Podaj miary kątów tego
równoległoboku.
 3. Obwód trapezu równoramiennego ABCD jest równy 14 cm. Ramię tego trapezu jest dwa
razy krótsze od krótszej podstawy i o 4 cm krótsze od dłuższej podstawy. Podaj długości
boków tego trapezu.
 4. Obwód trapezu równoramiennego ABCD jest równy 14 cm. Ramię tego trapezu jest o 2 cm
krótsze od krótszej podstawy i trzy razy krótsze od dłuższej podstawy. Podaj długości boków
tego trapezu.