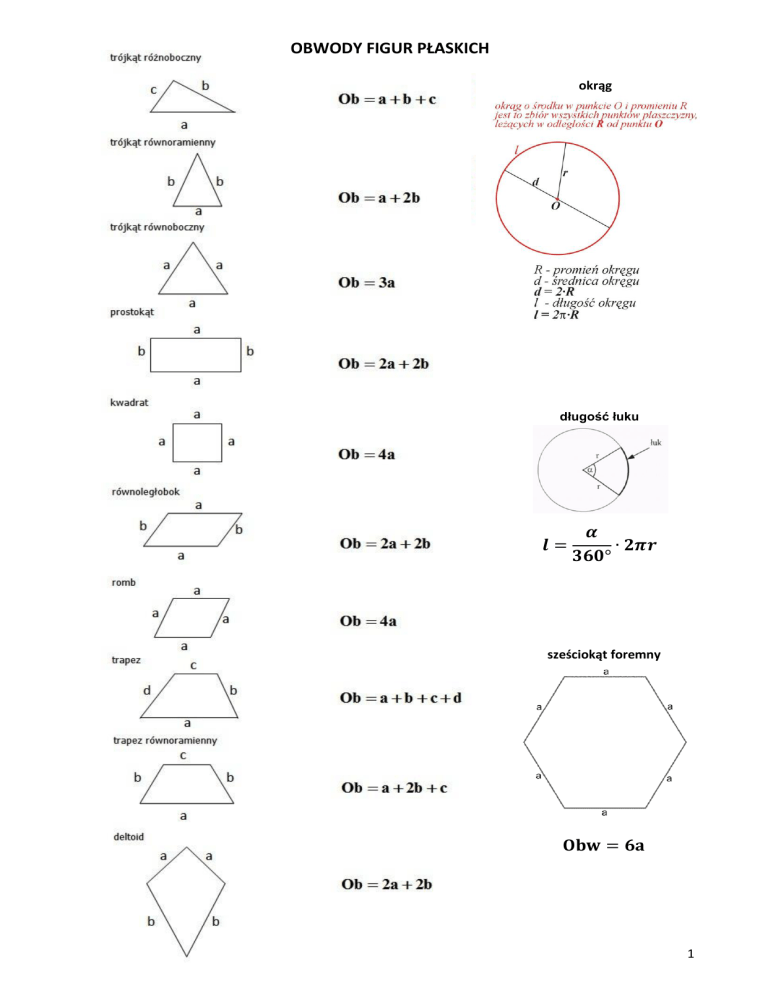
OBWODY FIGUR PŁASKICH
okrąg
długość łuku
𝒍=
𝜶
∙ 𝟐𝝅𝒓
𝟑𝟔𝟎°
sześciokąt foremny
𝐎𝐛𝐰 = 𝟔𝐚
1
POLA FIGUR PŁASKICH
sześciokąt foremny
lub ten sam wzór tylko w innej postaci
𝑷=
𝒂𝟐 𝟑
𝑷= 𝟔∙
𝟒
pole wycinka koła
𝜶
𝑷𝒘 =
∙ 𝝅𝒓𝟐
𝟑𝟔𝟎°
𝟏
𝒂+𝒃 ∙𝒉
𝟐
koło
długość łuku
𝒍=
𝜶
∙ 𝟐𝝅𝒓
𝟑𝟔𝟎°
2
POLA I OBJĘTOŚCI FIGUR PRZESTRZENNYCH
GRANIASTOSŁUP
- pole powierzchni całkowitej i pole powierzchni bocznej
=
+
=
∙
- objętośd graniastosłupa
=
∙
- pole podstawy,
- obwód podstawy,
- pole powierzchni bocznej
PROSTOPADŁOŚCIAN - szczególny przypadek graniastosłupa
- objętośd prostopadłościanu
=
∙
∙
- przekątna prostopadłościanu
=
+
+
SZEŚCIAN
- pole powierzchni całkowitej i pole powierzchni bocznej
=
- objętośd sześcianu
=
- przekątna sześcianu
=
OSTROSŁUP
- pole powierzchni całkowitej ostrosłupa
=
+
- objętośd ostrosłupa
=
∙
3
CZWOROŚCIAN FOREMNY
- pole powierzchni całkowitej
=
- objętośd czworościanu foremnego
=
- wysokośd czworościanu foremnego
=
BRYŁY OBROTOWE
WALEC
pole powierzchni całkowitej
=
+
=
+
objętośd
=
STOŻEK
pole powierzchni całkowitej
=
+
lub
=
+
=
objętośd
=
- tworząca stożka,
- promieo podstawy
KULA
pole powierzchni całkowitej (sfery)
=
objętośd
=
4
INNE PRZYDATNE WZORY I ZWIĄZKI
ZWIĄZKI MIAROWE W TRÓJKĄCIE 𝟑𝟎°, 𝟔𝟎°, 𝟗𝟎°
TWIERDZENIE PITAGORASA
LUB
=
+
ZWIĄZKI MIAROWE W TRÓJKĄCIE 𝟒𝟓°, 𝟒𝟓°, 𝟗𝟎°
TRÓJKĄT RÓWNOBOCZNY
- wysokośd trójkąta równobocznego
- promieo okręgu wpisanego w trójkąt równoboczny
=
czyli
=
- promieo okręgu opisanego na trójkącie równobocznym
=
czyli
=
Suma promieni okręgu wpisanego i opisanego na trójkącie równobocznym jest równa wysokości tego
trójkąta.
+
=
5
KWADRAT
=
- przekątna kwadratu
=
- promieo okręgu wpisanego w kwadrat
- promieo okręgu opisanego na kwadracie
SZEŚCIOKĄT FOREMNY
- promieo okręgu wpisanego w sześciokąt foremny - promieo okręgu opisanego na sześciokącie foremnym
- przekątne w sześciokącie
Miara kąta wewnętrznego n-kąta foremnego
=
𝜶 = 𝟏𝟖𝟎° −
=
czyli
𝟑𝟔𝟎°
𝒏
Suma miar kątów wewnętrznych n-kąta
𝜶 = 𝒏 − 𝟐 ∙ 𝟏𝟖𝟎°
=
Liczba przekątnych n-kąta
𝒅=
𝒏 𝒏−𝟑
𝟐
6
INNE WŁASNOŚCI
Jeżeli kąty oparte są na tym samym łuku AB,
to kąt środkowy AOB jest dwa razy większy
od kąta wpisanego ACB.
Kąt wpisany oparty na średnicy (lub półokręgu)
jest kątem prostym.
Jeżeli w kąt wpiszemy okrąg, to suma przeciwległych
kątów powstałego czworokąta AOBS jest równa 180ᴼ.
+
=
°
Odpowiednie odcinki trójkąta prostokątnego
utworzone po wpisaniu w niego okręgu mają
jednakową długośd.
Odcinki od punktów styczności do wierzchołków
trójkąta mają jednakową długośd.
|
|=|
|=
|
|=|
|=
|
|=|
|=
7
