TRYGONOMETRIA

SPOTKANIE 7
TRYGONOMETRIA
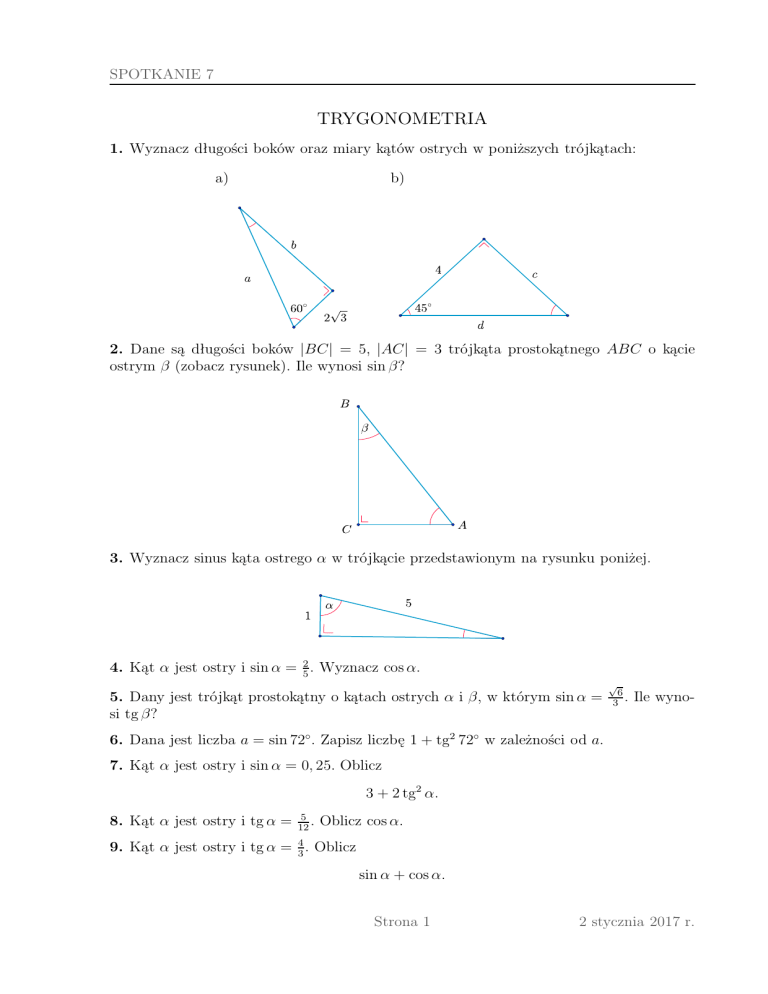
1. Wyznacz długości boków oraz miary kątów ostrych w poniższych trójkątach:
a)
b)
2. Dane są długości boków |BC| = 5, |AC| = 3 trójkąta prostokątnego ABC o kącie
ostrym β (zobacz rysunek). Ile wynosi sin β?
3. Wyznacz sinus kąta ostrego α w trójkącie przedstawionym na rysunku poniżej.
4. Kąt α jest ostry i sin α = 52 . Wyznacz cos α.
5. Dany jest trójkąt prostokątny o kątach ostrych α i β, w którym sin α =
si tg β?
√
6
.
3
Ile wyno-
6. Dana jest liczba a = sin 72◦ . Zapisz liczbę 1 + tg2 72◦ w zależności od a.
7. Kąt α jest ostry i sin α = 0, 25. Oblicz
3 + 2 tg2 α.
8. Kąt α jest ostry i tg α =
5
.
12
Oblicz cos α.
9. Kąt α jest ostry i tg α = 43 . Oblicz
sin α + cos α.
Strona 1
2 stycznia 2017 r.
SPOTKANIE 7
10. Drabinę o długości 4 metrów oparto o pionowy mur, a jej podstawę umieszczono w
odległości 1, 30 m od tego muru (zobacz rysunek).
Kąt α, pod jakim ustawiono drabinę spełnia warunek:
A. 0◦ < α < 30◦ ;
B. 30◦ < α < 45◦ ;
C. 45◦ < α < 60◦ ;
D. 60◦ < α < 90◦ ?
11. Jeżeli kąt α jest ostry i tg α = 34 , to ile wynosi wyrażenie
2 − cos α
?
2 + cos α
12. Kąt α jest ostry i
sin α
cos α
+
cos α
sin α
= 2. Oblicz wartość wyrażenia
sin α · cos α.
13. Kąty α i β są kątami ostrymi w trójkącie prostokątnym i cos α = 25 . Oblicz
tg α · sin β.
14. Dla pewnego kąta ostrego α funkcje trygonometryczne sin α i cos α mają wartości
sin α = a − 14 , cos α = a + 14 . Uzasadnij, że
√
4− 7
tg α =
3
.
15. Oblicz wartość wyrażenia
2 sin α − 3 cos α
,
3 cos α − 5 sin α
jeśli wiadomo, że α jest kątem ostrym oraz tg α = 3.
16. Kąt α jest kątem ostrym oraz cos α = 23 . Wykaż, że średnia arytmetyczna liczb
a = sin α, b = 21 oraz c = tg3α jest równa
√
5+1
.
6
√
√
17. Wykaż, że jeśli α i β są kątami ostrymi takimi, że sin α = 635 i tg β = 35, to
α = β.
Strona 2
2 stycznia 2017 r.