Kąty w wielościanach

252
STEREOMETRIA
Kąty w wielościanach
Aby móc rozważać kąty w wielościanach, trzeba dobrze rozumieć pewne pojęcia
dotyczące prostych i płaszczyzn w przestrzeni.
POŁOŻENIE PROSTYCH W PRZESTRZENI
Na płaszczyźnie, jeżeli dwie proste nie mają punktów wspólnych, to są równoległe.
W przestrzeni dwie proste, które nie mają punktów wspólnych, nie muszą być
równoległe.
Mówimy, że dwie proste w przestrzeni są równoległe, gdy albo nie mają punktów wspólnych i leżą
w jednej płaszczyźnie, albo się pokrywają.
Jeśli dwie proste w przestrzeni nie mają punktów
wspólnych i nie leżą w jednej płaszczyźnie, to mówimy, że są skośne.
Uwaga. Dwie proste, które przecinają się w przestrzeni,
zawsze leżą na jednej płaszczyźnie.
Na płaszczyźnie proste prostopadłe przecinają się. W przestrzeni proste prostopadłe nie muszą się przecinać.
Mówimy, że dwie proste w przestrzeni są prostopadłe, gdy istnieje prosta równoległa do jednej z nich,
przecinająca drugą pod kątem prostym.
Ćwiczenie A. Czy w prostopadłościanie można wskazać
dwie krawędzie, które są skośne, ale nie są prostopadłe?
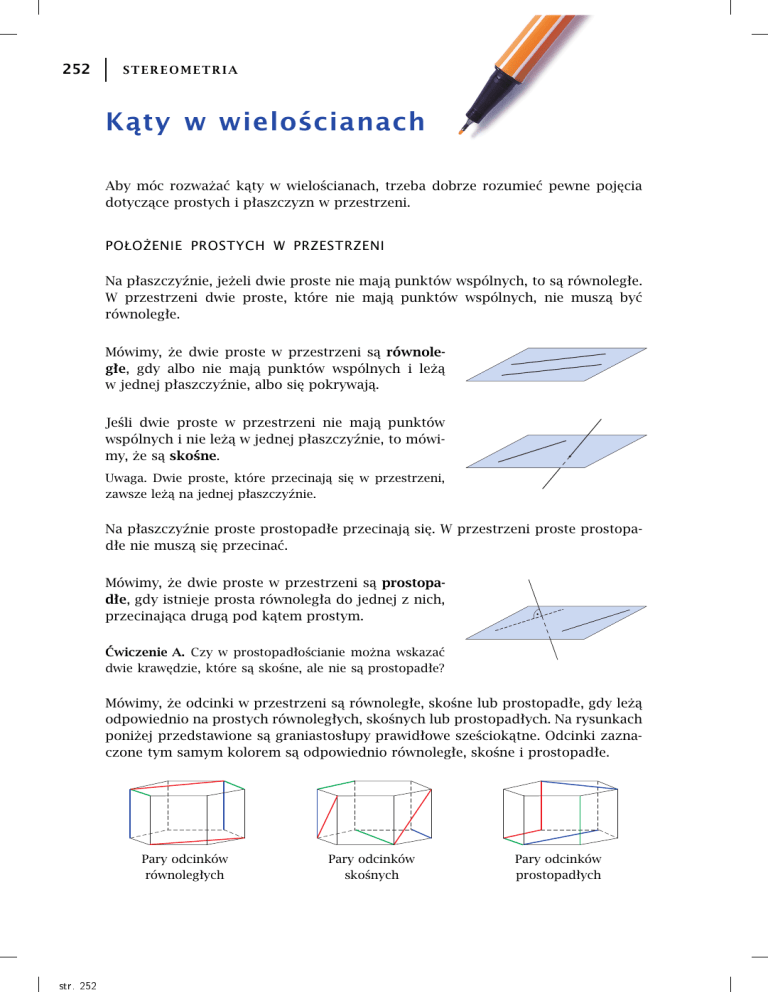
Mówimy, że odcinki w przestrzeni są równoległe, skośne lub prostopadłe, gdy leżą
odpowiednio na prostych równoległych, skośnych lub prostopadłych. Na rysunkach
poniżej przedstawione są graniastosłupy prawidłowe sześciokątne. Odcinki zaznaczone tym samym kolorem są odpowiednio równoległe, skośne i prostopadłe.
Pary odcinków
równoległych
Pary odcinków
skośnych
Pary odcinków
prostopadłych
KĄTY W WIELOŚCIANACH
Ćwiczenie B. Na rysunku obok przedstawiony jest prostopadłościan.
a) Które krawędzie są prostopadłe do krawędzi AA ?
b) Które krawędzie są skośne do odcinka AC?
c) Wymień wszystkie krawędzie skośne do przekątnej AC .
d) Wymień przekątne ścian oraz krawędzie prostopadłe
do odcinka AB .
PROSTA PROSTOPADŁA DO PŁASZCZYZNY
Mówimy, że prosta jest prostopadła do płaszczyzny, gdy jest prostopadła do każdej prostej leżącej
na tej płaszczyźnie.
Niech A będzie punktem wspólnym prostej k i płaszczyzny P. Aby stwierdzić, że prosta k jest prostopadła do płaszczyzny P, wystarczy wskazać dwie
proste leżące na tej płaszczyźnie i przechodzące
przez punkt A, do których prosta k jest prostopadła.
KĄT DWUŚCIENNY
Dwie półpłaszczyzny o wspólnej krawędzi dzielą
przestrzeń na dwie części. Każdą z tych części wraz
z tymi półpłaszczyznami nazywamy kątem dwuściennym.
Niech P będzie dowolną płaszczyzną prostopadłą do
krawędzi k kąta dwuściennego. Wspólna część płaszczyzny P i kąta dwuściennego to pewien kąt płaski.
Za miarę kąta dwuściennego przyjmujemy miarę tego kąta płaskiego.
Na rysunkach zaznaczono
kilka kątów między ścianami w graniastosłupie
prostym i w ostrosłupie.
253
254
STEREOMETRIA
KĄT MIĘDZY PROSTĄ A PŁASZCZYZNĄ
Niech prosta k przecina płaszczyznę P w punkcie
A. Na płaszczyźnie P możemy poprowadzić wiele
prostych przechodzących przez punkt A. Zauważ, że
prosta k tworzy z tymi prostymi różne kąty.
Spośród tych prostych wybierzmy taką prostą l,
która leży w płaszczyźnie F prostopadłej do płaszczyzny P i przechodzącej przez prostą k. Miara kąta
nachylenia prostej k do płaszczyzny P to miara kąta
(ostrego lub prostego) między prostymi k i l.
Uwaga. Kąt między prostą k a płaszczyzną P można wyznaczyć w następujący sposób: Przez dowolny punkt B
prostej k (B = A) prowadzimy prostą a prostopadłą do
płaszczyzny P. Znajdujemy punkt przecięcia prostej a
z płaszczyzną P — punkt C. Jeśli C = A, to kąt CAB jest
szukanym kątem nachylenia prostej k do płaszczyzny P.
Na poniższych rysunkach zaznaczono kilka kątów między odcinkami oraz kąty
między odcinkami i ścianami w graniastosłupie prostym i w ostrosłupie.
α — kąt nachylenia przekątnej graniastosłupa do podstawy
β — kąt między przekątną graniastosłupa
a krawędzią boczną
γ — kąt między przekątnymi sąsiednich
ścian bocznych
δ — kąt między przekątną ściany bocznej
a podstawą
α — kąt między krawędzią boczną a krawędzią podstawy
β — kąt nachylenia krawędzi bocznej do
podstawy
γ — kąt między wysokością ostrosłupa
a krawędzią boczną
δ — kąt między wysokością ostrosłupa
a ścianą boczną
KĄTY W WIELOŚCIANACH
przykłady
W graniastosłupie prawidłowym sześciokątnym √
krawędź podstawy ma długość 2, a wysokość tego graniastosłupa jest równa 2. Jaką miarę ma kąt między
przekątnymi ścian bocznych wychodzącymi z jednego wierzchołka?
√
√
|DC |2 = ( 2)2 + 22 = 6
√
|DC | = 6
|EC | = 2 3 = 3
2
EC to wysokość trójkąta równobocznego o boku 2.
√
sin α = |EC | = √3 =
Trójkąt ACD jest równoramienny.
√
1
= 2
2
2
|DC |
6
√
sin α = 2 , więc α = 45◦, czyli α = 90◦
2
2
2
2
Odp. W tym graniastosłupie przekątne ścian bocznych tworzą kąt prosty.
W graniastosłupie prostym, którego podstawa jest rombem, kąty nachylenia
przekątnych do podstawy wynoszą 30◦ i 60◦. Oblicz miary kątów między ścianami tego graniastosłupa.
tg 30◦ =
|AC | =
tg
α
2
=
h
|AC |
tg 60◦ =
h
tg 30◦
1
|DB|
2
1
|AC
|
2
|DB| =
|DB|
=
=
|AC |
α 1
α
tg 2 = 3 , więc 2 ≈ 18,435◦, czyli α ≈ 36,9◦
β = 180◦ − α ≈ 143,1◦
h
tg 60◦
h
tg 30◦
h
|DB|
h
tg 60◦
√
3
tg 30◦ √3
1
=
=
=
◦
tg 60
3
3
Odczytujemy z tablic trygonometrycznych lub obliczamy za
pomocą kalkulatora przybliżoną miarę kąta α
.
2
Odp. Kąty między ścianami tego graniastosłupa mają miary około 36,9◦ i 143,1◦.
255