Rodzaje Liczb Liczby Naturalne

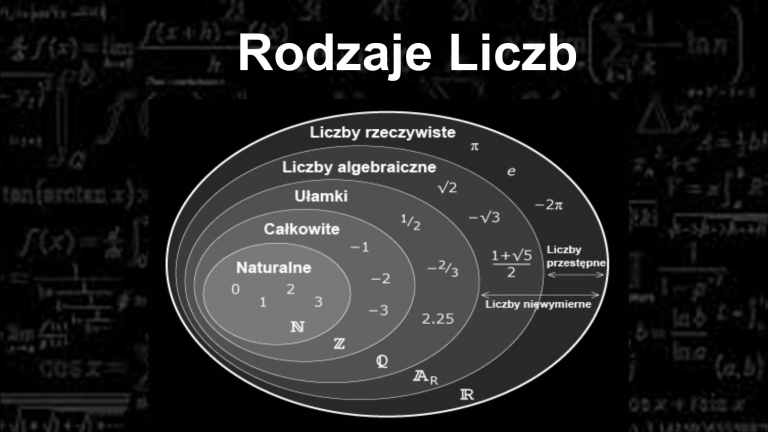
Rodzaje Liczb
Liczby Naturalne
Liczby naturalne - to liczby całkowite, dodatnie.
Zbiór liczb naturalnych oznaczamy symbolem N
N={1,2,3,4,5,6,...}
Ten sam zbiór możemy również zapisać wykorzystując symbol liczb całkowitych:
Z+={1,2,3,4,5,6,...}
Liczby Całkowite
Do liczb całkowitych zaliczamy liczby naturalne oraz ich ujemne odpowiedniki,
a także liczbę zero.
...−6,−5,−4,−3,−2,−1, 0, 1, 2, 3, 4, 5, 6, …
Zbiór liczb całkowitych oznaczamy symbolem
w Polsce
C
Liczby Wymierne
Liczba wymierna - to taka liczba, którą można zapisać w postaci ułamka
zwykłego, czyli w postaci: p/q gdzie:
p - to dowolna liczba całkowita
q - to liczba całkowita różna od 0.
Zbiór liczb wymiernych oznaczamy symbolem
w Polsce W
Liczby Niewymierne
Liczba niewymierna - to taka liczba, której nie można zapisać za pomocą
ułamka zwykłego.
Liczbami niewymiernymi są np.:
Zbiór liczb niewymiernych oznaczamy symbolem NW (w Polsce).
Liczby Rzeczywiste
Zbiór
liczb
rzeczywistych,
to
zbiór
wszystkich
niewymiernych.
Zbiór liczb rzeczywistych oznaczamy symbolem
Liczbami rzeczywistymi są np.:
liczb
wymiernych
i
Liczby Parzyste i Nieparzyste
Liczba parzysta - to taka liczba całkowita, którą można podzielić przez 2 (bez
reszty).
np: −62,−8,−6, 0, 2, 14, 22, 4536
Liczba nieparzysta - to taka liczba całkowita, której nie można podzielić przez
2 (przy dzieleniu przez dwa daje resztę 1).
np:−61,−7,−5, 1, 3, 15, 23, 4537
Liczby Przeciwne
Liczby przeciwne - to dwie liczby, których suma wynosi zero.
Np: Liczby 5 i −5 są liczbami przeciwnymi, ponieważ: 5+(−5)=5−5=0
Liczby Odwrotne
Liczby odwrotne - to dwie liczby, których iloczyn jest równy 1.
Np: Liczby 2 i 1/2 są odwrotne, ponieważ: 2⋅1/2=1
Liczby Pierwsze
Liczba pierwsza - to taka liczba naturalna, która ma dokładnie dwa dzielniki
naturalne: jedynkę i siebie samą.
W poniższej tabelce zaznaczono na żółto liczby pierwsze mniejsze od 100:
Liczby Złożone
Każdą liczbę naturalną większą od 1, która nie jest liczbą pierwszą, nazywamy
liczbą złożoną.
Każdą liczbę złożoną można rozłożyć na iloczyn mniejszych liczb naturalnych.
Mówiąc inaczej - liczba naturalna jest złożona, jeżeli można ją podzielić bez
reszty przez inną liczbę naturalną, większą od 1.
np:Liczba 6 jest złożona, ponieważ dzieli się przez 2 i przez 3. Oto jej rozkład
na iloczyn czynników: 6=2⋅3
Liczby Doskonałe
Liczba doskonała - to taka liczba naturalna, która jest równa sumie wszystkich
swoich podzielników, mniejszych od tej liczby.
Np: Liczba 6 jest doskonała, ponieważ: 1+2+3=6
Liczby 1, 2 i 3 to podzielnik liczby 6 mniejsze od 6.
Np:Liczba 28 jest doskonała, ponieważ: 1+2+4+7+14=28
Liczby 1, 2, 4, 7, 14 to podzielnik liczby 28 mniejsze od 28.
Liczby Algebraiczne
Liczba algebraiczna - to liczba rzeczywista, która jest pierwiastkiem pewnego
niezerowego wielomianu o współczynnikach wymiernych. Stopień takiego
wielomianu jest jednocześnie stopniem danej liczby algebraicznej.
Np: Liczba 10 jest algebraiczna, ponieważ jest pierwiastkiem wielomianu
W(x)=x−10.
Stopień tej liczby algebraicznej jest równy 1 (ponieważ wielomian W(x) ma
stopień 1).
Liczby Przestępne
Liczba przestępna - to taka liczba, która nie jest pierwiastkiem żadnego wielomianu o
współczynnikach wymiernych. Inaczej mówiąc jest to liczba niealgebraiczna.
Okazuje się, że nie tak łatwo jest udowodnić, że jakaś liczba jest przestępna.
Szczególnie dużo problemów sprawiły na tym polu ludziom liczby π i e.
Istnienie liczb przestępnych wykazał francuski matematyk Joseph Liouville w 1844 roku.
π – udowodnił to Ferdinand Lindemann w 1882 roku
e – udowodnił to Charles Hermite w 1873 roku.
Liczby Urojone
Liczba urojona – liczba, która podniesiona do kwadratu daje wartość ujemną.
Każda liczba urojona może zostać zapisana jako
jest liczbą rzeczywistą,
jest jedmostką urojoną spełniającą zależność
gdzie:
Liczba PI
Liczba π – stała matematyczna, która pojawia się w wielu
dziedzinach matematyki i fizyki.
Liczba π jest liczbą niewymierną, co udowodnił w roku 1761
Johann Heinrich Lambert. Co więcej, jest ona liczbą
przestępną, co w 1882 roku wykazał Ferdinand Lindemann.
Oznacza to, że nie jest możliwe zapisanie π za pomocą
skończonego zapisu złożonego z liczb całkowitych, działań
arytmetycznych, ułamków oraz potęg i pierwiastków.
Liczba Eulera
Liczbę Eulera (zwaną również pod nazwą liczby Nepera) oznaczamy literą e. Wartość tej liczby można
określić w przybliżeniu:
e=2,71828182845904523536028747135266249775724709369995…
Liczbę e można definiować na wiele różnych sposobów. Najczęściej spotykana jest definicja wykorzystująca
następującą granicę:
Równie często definiuje się liczbę e jako sumę szeregu:
Jest liczbą niewymierną
Złota liczba
Złota liczba - dzieli odcinek na dwie części tak, by stosunek długości dłuższej z
nich do krótszej był taki sam, jak całego odcinka do części dłuższej. Innymi
słowy: długość dłuższej części ma być średnią geometryczną długości krótszej
części i całego odcinka. Jest liczbą niewymierną.
KONIEC
Sebastian Suszka
Rafał Prokopowicz