Karta pracy 1 Własności kątów

Karta pracy 1
WŁASNOŚCI KĄTÓW
kółko matematyczne – II klasa gimnazjum
Uczniowie .................................................................................................................................
Lp.
1.
2
3
4
Rysunek
Treść zadania
A
B
C
D
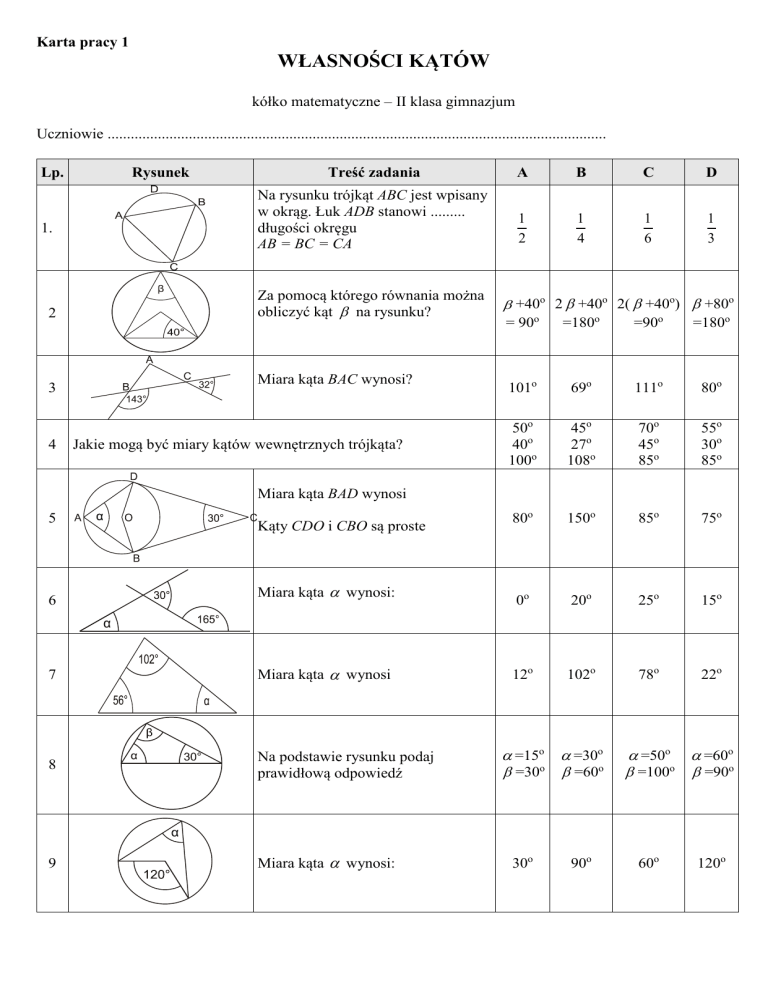
Na rysunku trójkąt ABC jest wpisany
w okrąg. Łuk ADB stanowi .........
długości okręgu
AB = BC = CA
1
2
1
4
1
6
1
3
Za pomocą którego równania można
obliczyć kąt  na rysunku?
Miara kąta BAC wynosi?
Jakie mogą być miary kątów wewnętrznych trójkąta?
 +40o 2  +40o 2(  +40o)  +80o
= 90o
=180o
=90o
=180o
101o
69o
111o
80o
50o
40o
100o
45o
27o
108o
70o
45o
85o
55o
30o
85o
80o
150o
85o
75o
0o
20o
25o
15o
12o
102o
78o
22o
Miara kąta BAD wynosi
5
6
Kąty CDO i CBO są proste
Miara kąta  wynosi:
7
Miara kąta  wynosi
8
Na podstawie rysunku podaj
prawidłową odpowiedź
9
Miara kąta  wynosi:
 =15o  =30o
 =30o  =60o
30o
90o
 =50o  =60o
 =100o  =90o
60o
120o
Karta pracy 2
Własności kątów – zadania tekstowe
kółko matematyczne – II klasa gimnazjum
Uczniowie ............................................................................................................................................
Zadanie 1
Wyznacz miarę kąta DFE, jeśli A i B są środkami mniejszych okręgów, a C środkiem większego okręgu.
Zadanie 2
Dane są 3 punkty na okręgu: A, B, C. Te trzy punkty dzielą okrąg w stosunku 2 : 3 : 4. Określ położenie środka
okręgu opisanego na trójkącie ABC.
Zadanie 3
W trójkącie prostokątnym miara kąta utworzonego przez wysokość opuszczoną z wierzchołka kąta prostego i
jedną z przyprostokątnych jest równa 32o. Oblicz miary kątów trójkąta.
Zadanie 4
Trójkąt równoramienny, w którym miara kąta zawartego między ramionami wynosi 36o, podziel na dwa
trójkąty równoramienne.
Zadanie 5
W trójkącie prostokątnym ABC, gdzie kąt przy wierzchołku C jest prosty, dwusieczna kąta prostego dzieli
przeciwprostokątną na odcinki o długościach 20 cm i 15 cm. Oblicz długość odcinka dwusiecznej zawartego
między wierzchołkiem kąta prostego a przeciwprostokątną.
Zadanie 6
Trójkąt prostokątny o kącie ostrym 40o wpisany jest w koło. Oblicz kąt zawarty między wysokością a środkową
wychodzącymi z wierzchołka kąta prostego.
Zadanie 7
Suma kątów wpisanego i środkowego opartych na tym samym łuku wynosi 96o. Oblicz miary tych kątów.
Zadanie 8
Trójkąt równoramienny ABC jest wpisany w okrąg tak, że bok AB jest średnicą okręgu. Miara kąta CAB
wynosi 72o. Oblicz miarę kąta ABC.
Zadanie 9
W okrąg wpisano trójkąt ABC, którego kąty przy wierzchołkach A i B mają miary: 50o i 70o. Jaką część tego
okręgu stanowi łuk ABC?
Zadanie 10
Dane są dwa okręgi o promieniach różnej długości styczne zewnętrznie w punkcie S i prosta przechodząca
przez punkt S, przecinająca jeden z okręgów w punkcie P, a drugi w punkcie R. Udowodnij, że kąty środkowe
oparte na łukach SP i SR są równe.
Źródło:
1. B i S. Biernat, M. Bierówka, I. Rutkowska, Testy sprawdzające wielostopniowe z matematyki dla gimnazjum, wyd. Nowik,
Opole, 2001;
2. K. Dworecka, Z. Kochanowski, Konkursy matematyczne wybór zadań, WSiP, Warszawa, 1993;
3. P. Nodzyński, Z. Bobiński, Liga zadaniowa, wyd. Czarny Kruk, Bydgoszcz, 1996.