Okręgi i proste – ćwiczenie Zad.1. Kąt środkowy oparty na łuku

Okręgi i proste – ćwiczenie
Zad.1. Kąt środkowy oparty na łuku, którego długość jest równa
A)
B)
C)
D)
długości okręgu, ma miarę:
Zad.2.W okręgu o środku w punkcie kąt środkowy i kąt wpisany oparte są na tym samym
łuku wyznaczonym przez punkty i leżące na okręgu. Suma miar tych kątów jest równa kątowi
prostemu. Wierzchołek kąta znajduje się w punkcie . Wynika stąd, że trójkąt:
A)
jest równoboczny
B)
jest prostokątny
C)
jest równoboczny
D)
jest prostokątny
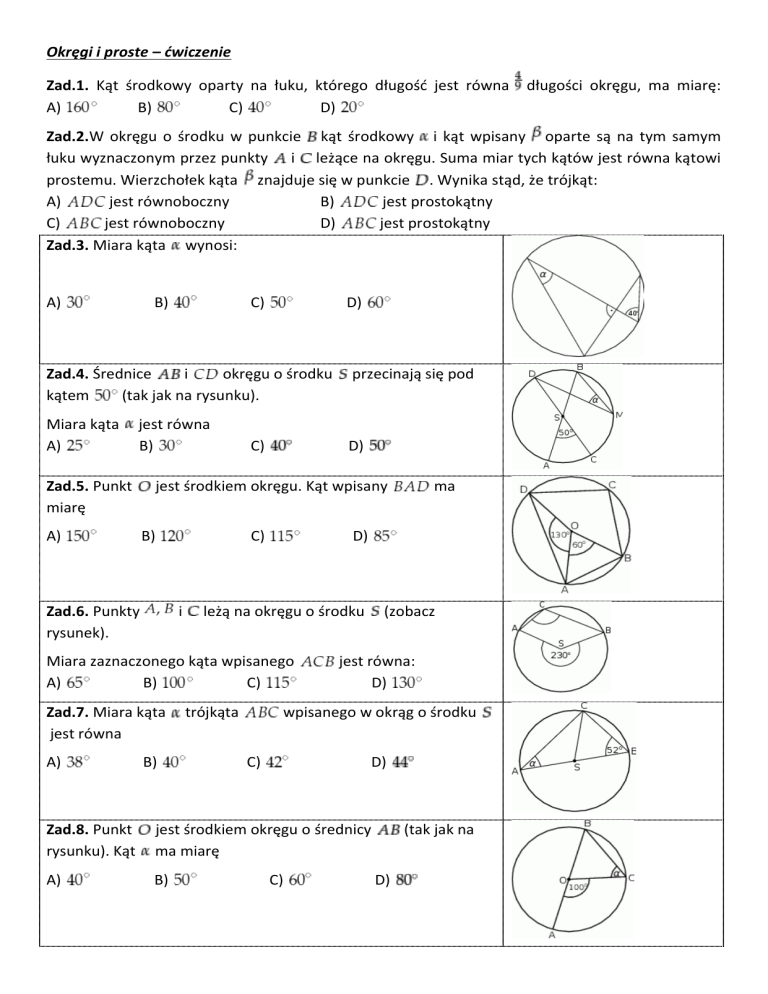
Zad.3. Miara kąta wynosi:
A)
B)
C)
D)
Zad.4. Średnice
i
okręgu o środku
kątem
(tak jak na rysunku).
Miara kąta
A)
jest równa
B)
Zad.5. Punkt
miarę
A)
C)
D)
jest środkiem okręgu. Kąt wpisany
B)
Zad.6. Punkty
rysunek).
C)
i
Zad.7. Miara kąta
jest równa
leżą na okręgu o środku
B)
trójkąta
ma
D)
Miara zaznaczonego kąta wpisanego
A)
B)
C)
A)
przecinają się pod
(zobacz
jest równa:
D)
wpisanego w okrąg o środku
C)
D)
Zad.8. Punkt
rysunku). Kąt
jest środkiem okręgu o średnicy
ma miarę
A)
B)
C)
(tak jak na
D)
Zad.9. Punkt
miarę
jest środkiem okręgu. Kąt środkowy
A)
B)
C)
ma
D)
Zad.10. Przez okrąg poprowadzono dwie sieczne, które przecięły się na zewnątrz tego okręgu
w punkcie P. Odcinek leżący wewnątrz okręgu (wewnętrzny) pierwszej siecznej ma długość 3, a jej
odcinek leżący na zewnątrz (zewnętrzny) ma długość 2. Oblicz długości odcinków drugiej siecznej,
jeżeli wiadomo, że odcinek wewnętrzny drugiej siecznej jest o 8 dłuższy od odcinka zewnętrznego.
Zad.11. W kąt wpisano dwa okręgi styczne
zewnętrznie. Promień mniejszego okręgu ma
długość 2, a większego 5. Oblicz długość
odcinka łączącego wierzchołek tego kąta ze
środkiem mniejszego okręgu.
Zad.12. Kąt  między styczną a cięciwą okręgu
ma miarę 300. Oblicz miarę kąta .
Zad.13. Na czworokącie ABCD opisano okrąg. Punkt S jest środkiem tego okręgu, a odcinek AC jego
średnicą. Styczna do okręgu w punkcie B jest równoległa do odcinka AC. Kąt ASD ma miarę 40 0.
Oblicz miary wszystkich kątów wewnętrznych tego czworokąta.
Zad.14. Oblicz x i podaj długości zaznaczonych odcinków siecznych i stycznych:
a)
b)
4
x+6
x+4
x
15
2x+2
c)
x+3
d)
x-2,5
3x+1
x+4
x-2
x+2
x
2x+4