B.Skrypt (R).009.05(ROZWIĄZ.ZAD.2.Dwa układy planet z 7 czy 8

ZADANIE DO ROZWIĄZ. Z DWOMA UKŁADAMI PLANET, W KTÓRYCH 7 CZY 8 PLANET KRĄŻY WOKÓŁ DWÓCH GWIAZD W DWÓCH PŁASZCZYZNACH.
str.1
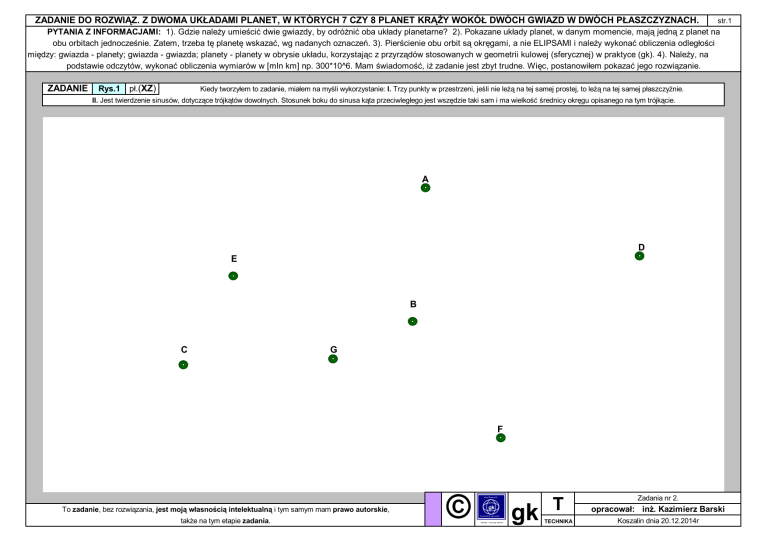
PYTANIA Z INFORMACJAMI: 1). Gdzie należy umieścić dwie gwiazdy, by odróżnić oba układy planetarne? 2). Pokazane układy planet, w danym momencie, mają jedną z planet na
obu orbitach jednocześnie. Zatem, trzeba tę planetę wskazać, wg nadanych oznaczeń. 3). Pierścienie obu orbit są okręgami, a nie ELIPSAMI i należy wykonać obliczenia odległości
między: gwiazda - planety; gwiazda - gwiazda; planety - planety w obrysie układu, korzystając z przyrządów stosowanych w geometrii kulowej (sferycznej) w praktyce (gk). 4). Należy, na
podstawie odczytów, wykonać obliczenia wymiarów w [mln km] np. 300*10^6. Mam świadomość, iż zadanie jest zbyt trudne. Więc, postanowiłem pokazać jego rozwiązanie.
ZADANIE
Rys.1
pł.(XZ)
Kiedy tworzyłem to zadanie, miałem na myśli wykorzystanie: I. Trzy punkty w przestrzeni, jeśli nie leżą na tej samej prostej, to leżą na tej samej płaszczyźnie.
II. Jest twierdzenie sinusów, dotyczące trójkątów dowolnych. Stosunek boku do sinusa kąta przeciwległego jest wszędzie taki sam i ma wielkość średnicy okręgu opisanego na tym trójkącie.
A
D
E
B
C
G
F
To zadanie, bez rozwiązania, jest moją własnością intelektualną i tym samym mam prawo autorskie,
także na tym etapie zadania.
©
skrypt Romany (R)
gk
dla wszystkich ludzi świata
Romana - imię mojej małżonki
gk
Zadania nr 2.
T
opracował: inż. Kazimierz Barski
TECHNIKA
Koszalin dnia 20.12.2014r
ROZWIĄZANIE ZAD. Z DWOMA UKŁADAMI PLANET, W KTÓRYCH 7 CZY 8 PLANET KRĄŻY WOKÓŁ DWÓCH GWIAZD W DWÓCH PŁASZCZYZNACH.
str.2
Jasne, że poszedłem na łatwiznę. Najpierw narysowałem dwa okręgi, potem dwie ELIPSY, a potem rozmieściłem planety. Oczywiście, w centralnych punktach okręgów umieściłem
gwiazdy. Okręgi i ELIPSY posłużą mi do wykonania odczytów.
Rys.2
pł.(XZ)
24h;0h
24h;0h
24h;0h
E
A
A
D
D
G2
24h;0h
E
18h
18h
6h
r=
91,673247220931700
6h
[mln km]
G1
18h 18h
B
C
6h
6h
B'
B
G
12h
r=
91,673247220931700
[mln km]
F
F
12h
12h
G
C
12h
©
skrypt Romany (R)
gk
dla wszystkich ludzi świata
gk
Rozwiązanie Zadania nr 2 - w pełni
T
opracował: inż. Kazimierz Barski
TECHNIKA
Koszalin dnia 20.12.2014r
ROZWIĄZANIE ZAD. Z DWOMA UKŁADAMI PLANET, W KTÓRYCH 7 CZY 8 PLANET KRĄŻY WOKÓŁ DWÓCH GWIAZD W DWÓCH PŁASZCZYZNACH.
Rys.3
pł.(XZ)
str.3
24h;0h
24h;0h
24h;0h
E
A
(AA)
A
(AD)
(AB)
D
E
(DD)
D
G2
24h;0h
18h
(DG2)
18h
6h
6h
(BG2)
G1
(BG2)
18h 18h
B
6h
6h
(BB) B'
B
(DF)
C
G
12h
F
F
12h
12h
(FF)
G
C
12h
©
skrypt Romany (R)
gk
dla wszystkich ludzi świata
gk
Rozwiązanie Zadania nr 2 - w pełni
T
opracował: inż. Kazimierz Barski
TECHNIKA
Koszalin dnia 29.12.2014r
ROZWIĄZANIE ZAD. Z DWOMA UKŁADAMI PLANET, W KTÓRYCH 7 CZY 8 PLANET KRĄŻY WOKÓŁ DWÓCH GWIAZD W DWÓCH PŁASZCZYZNACH.
Rys.4
pł.(XZ)
str.4
24h;0h
24h;0h
24h;0h
E
A
(AA)
A
(EE)
(AD)
B"'
B"
D
3
D
G2
24h
0h
18h
18h
E
(EG1)
6h
6h
(BG2)
1
G1
18h 18h
(DG2)
2
(B'G1)
(B'B')
B'
(G1H)
(BH)
C
B'
B
(BG2)
Trzy trójkąty równoramienne nr2, dwa (1 i 3)
z nich są odchylone i wszystkie zielone.
(DF)
H
12h
Dwa trójkąty równoramienne nr1
odchylone, żółte
(CC)
F
2*r
F
12h
12h
H
(FF)
C
12h
⌂1
⌂1
Ucz się widzieć przestrzeń, wykorzystując swoją wyobraźnię, tak jak ja to robię.
©
skrypt Romany (R)
gk
dla wszystkich ludzi świata
gk
Rozwiązanie Zadania nr 2 - w pełni
T
opracował: inż. Kazimierz Barski
TECHNIKA
Koszalin dnia 29.12.2014r
ROZWIĄZANIE ZAD. Z DWOMA UKŁADAMI PLANET, W KTÓRYCH 7 CZY 8 PLANET KRĄŻY WOKÓŁ DWÓCH GWIAZD W DWÓCH PŁASZCZYZNACH.
Rys.5
str.5
pł.(XY) MAPA
D
E
Liniał b.przydatny
Ślad orbity wokół gwiazdy G2
Orbita planet krążących wokół gwiazdy G1. Jej rzut prostokątny
jest ELIPSĄ, ponieważ zachowuje odchylenie względem rzutni.
⌂1
Albo, jeszcze inaczej. Okrąg nie jest równoległy do pł.(XY) rzutu.
Średnica KULI wg tarczy z.(24h)
G2
18h 19h 20h
21h
22h
23h
17h 16h
15h
14h
13h
24h
0h
1h
2h
3h
4h
5h
11h
10h
9h
8h
7h
6h
12h
G1
C
(CG1)
F
H
B'
Trójkąt: (B:G1:H) równoramienny lekko odchylony w stosunku od rzutni i pokazaną wysokością.
(BB')
A
Trójkąt niebieski równoramienny,
⌂1
równoległy do rzutni pł.(XY).
B
(CC)
H
WNIOSKI: 1). Na rys.1 pokazałem zbiór planet, które mają poruszać się po okręgach, bo ich
C
orbitami są okręgi. 2). Korzystając z pewnika i twierdzenia Talesa określiłem dwa okręgi na
rys.2. Jednocześnie w miejscach centralnych okręgów wstawiłem gwiazdy G1 i G2. Rys.2
przedstawia linie przerywane w poprzek osi dużych ELIPS i "dodatkowe planety" na okręgach
średnic KUL(niebieskie linie przerywane długie). Chciałbym przypomnieć, iż wymiary niebieskie są wym.rzeczywistymi. 4). Rys.3 przedstawia otoczenie planet wokół gwiazdy
G2. Poza tym, są tu wymiary rzeczywiste związane z średn.KULI i wymiary związane z ELIPSĄ. Korzystając ze sposobności pokazania przestrzeni narysowałem trójkąty żółte
i zielone z opisami. Rys.4 zamyka rzutnie pł.(XZ). Postanowił pokazać orbity planet w innym ujęciu, na pł.(XY)MAPA. 5). Rys.5 jest widokiem z góry. Pokazuje ślad orbity planet otaczających gwiazdę G2, gdy tymczasem orbita gwiazdy G1 jest niemal w pełni rozwinięta. Ma niewielkie odchylenie od swojej rzutni. Dlatego dla porównania pokazałem
dwa trójkąty. Na płaszczyźnie rzutni obrys niebieski trójkąta, a na ELIPSIE pokazałem pole żółte trójkąta. Jest jeszcze coś, co wymaga wyjaśnienia. Chodzi o dwie planety 2*B.
Może mieć charakter odkrywczy-odkryto ukrytą planetę. Z rzutni rys.1 wcale nie wynika, że jest coś
Rozwiązanie Zadania nr 2 - w pełni
gk
ukryte.Można też uznać jedną z nich B. Czerwona strzałka wskazuje rzeczywistą odległ.obu planet.
opracował: inż. Kazimierz Barski
©
skrypt Romany (R)
dla wszystkich ludzi świata
gk
T
TECHNIKA
Koszalin dnia 30.12.2014r
ROZWIĄZANIE ZAD. Z DWOMA UKŁADAMI PLANET, W KTÓRYCH 7 CZY 8 PLANET KRĄŻY WOKÓŁ DWÓCH GWIAZD W DWÓCH PŁASZCZYZNACH.
str.6
Z PLIKU MOGĄ KORZYSTAĆ ZA DARMO OSOBY NIEPEŁNOSPRAWNE.
Przyrząd: OKRĄGŁA LINIJKA
pod nazwą:
r=
Przyrząd 24h
"Słońce Majów"
Obwód wewnętrzny koła:
Promień koła:
Rys.2
r=
575 [mln km]
576/(2*π)
91,514092277839800
[mln km]
23h
Kto chce poznać obliczenia z odczytów wymiarów rzeczyw., niech szuka pliku B.Skrypt (R).009.03
24h;0h
Odczyty wymiarów: Lp. 23
1h
Pełne godz.
5 [h]
[mln km]
22h
2h
Średnica koła: Ø= 2*r tj.
183,02818455568000
Średnia artm.
3,00
[mln km]
Odczyt prawy:
3,20
[mln km]
Odczyt lewy:
2,80
[mln km]
24h
[mln km]
21h
3h
20h
4h
19h
5h
18h
6h
O
17h
7h
16h
8h
15h
9h
14h
10h
13h
12h
11h
©
skrypt Romany (R)
gk
dla wszystkich ludzi świata
gk
Rozwiązanie Zadania nr 2 - w pełni
T
opracował: inż. Kazimierz Barski
TECHNIKA
Koszalin dnia 30 grudnia 2014r
ROZWIĄZANIE ZAD. Z DWOMA UKŁADAMI PLANET, W KTÓRYCH 7 CZY 8 PLANET KRĄŻY WOKÓŁ DWÓCH GWIAZD W DWÓCH PŁASZCZYZNACH.
1 2 3 … kolejne formuły matem.
1 formuła łuku: 2*((n)[h]*24[mm/h]+…....[mm])=
3 formuła kąta: Ł/r [rad] → 4 formuła kąta: (=stopnie(3)
str.7
OZNACZENIA:
5
formuła pół kąta:
9
(=`3/2
→
6
formuła pół kąta:
(=stopnie(5)
10
podać ilość razy (n) przekracza pełny wymiar 2*r
7
formuła strzałki łuku Ł:
formuła wymiaru, w tym wymiaru > 2*r:
r*(1-cos(5))
8
formuła wymiaru cięciwy:
13 14
2*r*(n)+cięciwa(odczyt:h;mm)
2*(7*(2*r-7))^0,5
kąt skorygowany &s o kol.(ab:ac).
Jeśli chcesz poznać pełny wynik obliczeń musisz wpisać znak równości w komórkę o kolorze beżowym. Dot.każdej komórki w tej tabeli. Wychodzi się z niej przyciskiem enter.
I. TABELA OBLICZENIOWA DOTYCZĄCA ROZWIĄZYWANIA ZADAŃ ZWIĄZANYCH WYMIARAMI - DŁUGOŚCI I KĄTA &s.
Ł (łuk)
r
kąt: &
kąt: &/2
Strzałka łuku Ł
Cięciwa łuku Ł
n(2*r)
WYMIAR:
Odczyt
wymiaru (n)
[mm]
1
2
3
4
5
6
7
8
9
10
Lp. Nazwa
x
odcinka
[h]
a
(b:c)
d
(e:f)
1
(AB)str.3
(AD)str.3
(AF)str.3
(BB)str.3
(DF)str.3
(AA)str.3
(BG2)str.3
(DD)str.3
(FF)str.3
(B'G1)str4
(EG1)str4
(CG1)str4
(G1H)str4
(BH)str.4
(EE)str.4
(CC)str.4
(HH)str.4
(BB')str.5
(EG1)str.5
(CC)str.5
(HH)str.5
(CG1)str.5
(BD)str.5
1
4
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
[mln km] [mln km] [mln km]
13
2,421644337142130000
Warunek 1: Warunek 2:
Kąt &s
11
12
13
14
[rad]
[°]
[rad]
[°]
[mln km]
[mln km]
[szt]
[mln km]
&/2 < 90°
(m:n)
(o:p)
(q:r)
(s:v)
(w:aa)
(ab:ac)
(ad:ah)
(ai:ak)
(al:an)
ao
(ap:aq)
PRAWDA
PRAWDA
PRAWDA
PRAWDA
PRAWDA
PRAWDA
PRAWDA
PRAWDA
PRAWDA
PRAWDA
PRAWDA
PRAWDA
PRAWDA
PRAWDA
PRAWDA
PRAWDA
PRAWDA
PRAWDA
PRAWDA
PRAWDA
PRAWDA
PRAWDA
PRAWDA
PRAWDA
PRAWDA
PRAWDA
PRAWDA
PRAWDA
PRAWDA
PRAWDA
PRAWDA
PRAWDA
PRAWDA
PRAWDA
PRAWDA
PRAWDA
PRAWDA
PRAWDA
PRAWDA
PRAWDA
PRAWDA
PRAWDA
PRAWDA
PRAWDA
PRAWDA
PRAWDA
0,8
47,500
(g:h)
(i:j)
(k:l)
14,00
76,00
91,6732
0,82903
47,500
0,41452
23,750
7,763671711458
73,84219373366390
0
73,84219373366390
15,00
222,00
91,6732
2,42164
138,750
1,21082
69,375
59,381341494263
171,59507079831900
0
171,59507079831900
3
15,50
175,00
91,6732
1,90895
109,375
0,95448
54,688
38,682840871340
149,61284825756400
0
149,61284825756400
0
15,20
30,40
91,6732
0,33161
19,000
0,16581
9,500
1,257243440764
30,26089995057760
0
30,26089995057760
3
14,65
173,30
91,6732
1,89041
108,313
0,94520
54,156
37,991518839435
148,62377056185000
0
148,62377056185000
0
13,50
27,00
91,6732
0,29452
16,875
0,14726
8,438
0,992224477792
26,90251811918190
0
26,90251811918190
1
7,55
63,10
91,6732
0,68831
39,438
0,34416
19,719
5,375702694157
61,86171884710170
0
61,86171884710170
0
15,70
31,40
91,6732
0,34252
19,625
0,17126
9,813
1,341111669579
31,24673056574500
0
31,24673056574500
0
3,80
7,60
91,6732
0,08290
4,750
0,04145
2,375
0,078746706097
7,59782375897051
0
7,59782375897051
1
6,25
60,50
91,6732
0,65995
37,813
0,32998
18,906
4,945769919215
59,40804446908970
0
59,40804446908970
0
12,35
24,70
91,6732
0,26944
15,438
0,13472
7,719
0,830623811652
24,62535507559670
0
24,62535507559670
0
17,65
35,30
91,6732
0,38506
22,063
0,19253
11,031
1,693849588107
35,08231792023310
0
35,08231792023310
1
3,65
55,30
91,6732
0,60323
34,563
0,30161
17,281
4,138307851865
54,46535213083390
0
54,46535213083390
0
22,20
44,40
91,6732
0,48433
27,750
0,24216
13,875
2,674914573486
43,96730794600500
0
43,96730794600500
1
9,60
67,20
91,6732
0,73304
42,000
0,36652
21,000
6,088897982031
65,70550726944940
0
65,70550726944940
1
8,05
64,10
91,6732
0,69922
40,063
0,34961
20,031
5,545687103328
62,80215423753240
0
62,80215423753240
1
3,80
55,60
91,6732
0,60650
34,750
0,30325
17,375
4,182984372683
54,75173651216570
0
54,75173651216570
0
20,55
41,10
91,6732
0,44833
25,688
0,22417
12,844
2,293673840883
40,75664944180350
0
40,75664944180350
1
21,95
91,90
91,6732
1,00247
57,438
0,50124
28,719
11,276821117005
88,09991885911970
0
88,09991885911970
1
19,35
86,70
91,6732
0,94575
54,188
0,47288
27,094
10,059993741049
83,50475704912960
0
83,50475704912960
1
13,40
74,80
91,6732
0,81594
46,750
0,40797
23,375
7,523822626249
72,74224622360440
0
72,74224622360440
0
12,50
25,00
91,6732
0,27271
15,625
0,13635
7,813
0,850891980692
24,92260376813410
0
24,92260376813410
5
3,00
246,00
91,6732
2,68344
153,750
1,34172
76,875
70,856428821776
178,55693016813000
0
178,55693016813000
cięciwa<2*r [rad]
[°]
2,4 138,750
1,9 109,375
0,3
19,000
1,9 108,313
0,3
16,875
0,7
39,438
0,3
19,625
0,1
4,750
0,7
37,813
0,3
15,438
0,4
22,063
0,6
34,563
0,5
27,750
0,7
42,000
0,7
40,063
0,6
34,750
0,4
25,688
1,0
57,438
0,9
54,188
0,8
46,750
0,3
15,625
2,7 153,750
Przedstawione materiały w tym pliku stanowią początek głębokiej analizy dla każdego naukowca na świecie. Np. Trójkąty odchylone będące w przestrzeni można śmiało rozwiązywać
znanymi metodami geometrii euklidesowej. W kolorze niebieskim strzałki z podwójnymi grotami przypisane bokom jednego trójkąta, które mogą stać się wymiarami odchylonymi tego
samego trójkąta mając kolor fioletowy. Czy też trójkąta zachowującego te same kąty (podobnego) lub zachowującego cechy trójkąta równoramiennego. Wszystko to o czym mówię
sprowadza się do doskonalenia własnej wyobraźni. Żeby być mistrzem w tej dziedzinie, trzeba bardzo dużo pracować nad sobą. Do tego stopnia, żeby w każdym momencie dać odpór
wszelkim zarzutom. Kiedy się ma wiarę w wykonane dzieło, wówczas nabiera się szacunek do samego siebie. Jednocześnie należy pamiętać, że zawsze jest ktoś od nas lepszy !!!
©
skrypt Romany (R)
gk
dla wszystkich ludzi świata
gk
Rozwiązanie Zadania nr 2 - w pełni
T
opracował: inż. Kazimierz Barski
TECHNIKA
Koszalin dnia 30 grudnia 2014r