Kolokwium II – Algorytmy i Struktury Danych – 13

Imię Nazwisko:
Nr indeksu:
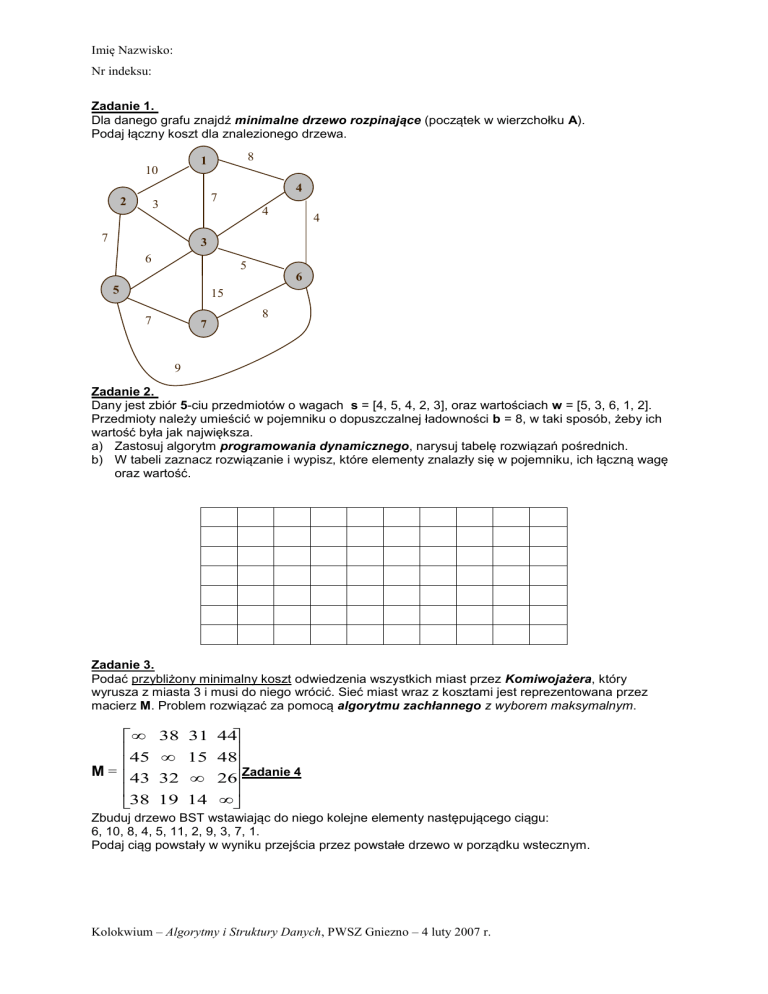
Zadanie 1.
Dla danego grafu znajdź minimalne drzewo rozpinające (początek w wierzchołku A).
Podaj łączny koszt dla znalezionego drzewa.
2
8
1
10
4
7
3
4
7
4
3
6
5
6
5
15
7
7
8
9
Zadanie 2.
Dany jest zbiór 5-ciu przedmiotów o wagach s = [4, 5, 4, 2, 3], oraz wartościach w = [5, 3, 6, 1, 2].
Przedmioty należy umieścić w pojemniku o dopuszczalnej ładowności b = 8, w taki sposób, żeby ich
wartość była jak największa.
a) Zastosuj algorytm programowania dynamicznego, narysuj tabelę rozwiązań pośrednich.
b) W tabeli zaznacz rozwiązanie i wypisz, które elementy znalazły się w pojemniku, ich łączną wagę
oraz wartość.
Zadanie 3.
Podać przybliżony minimalny koszt odwiedzenia wszystkich miast przez Komiwojażera, który
wyrusza z miasta 3 i musi do niego wrócić. Sieć miast wraz z kosztami jest reprezentowana przez
macierz M. Problem rozwiązać za pomocą algorytmu zachłannego z wyborem maksymalnym.

45
M= 
43

38
38 31 44
 15 48
 Zadanie 4
32  26

19 14 
Zbuduj drzewo BST wstawiając do niego kolejne elementy następującego ciągu:
6, 10, 8, 4, 5, 11, 2, 9, 3, 7, 1.
Podaj ciąg powstały w wyniku przejścia przez powstałe drzewo w porządku wstecznym.
Kolokwium – Algorytmy i Struktury Danych, PWSZ Gniezno – 4 luty 2007 r.
Imię Nazwisko:
Nr indeksu:
Zadanie 5
Przekształć dane drzewo binarne w stóg.
5
7
6
3
1
2
8
4
9
Kolokwium – Algorytmy i Struktury Danych, PWSZ Gniezno – 4 luty 2007 r.