RZĄD I

RZĄD I
1.
RZĄD II
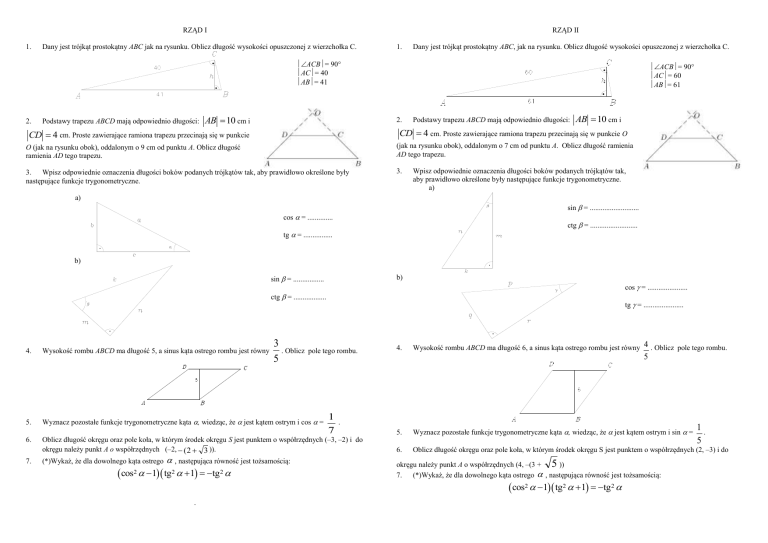
Dany jest trójkąt prostokątny ABC jak na rysunku. Oblicz długość wysokości opuszczonej z wierzchołka C.
1.
Dany jest trójkąt prostokątny ABC, jak na rysunku. Oblicz długość wysokości opuszczonej z wierzchołka C.
ACB= 90
AC= 40
AB= 41
2.
Podstawy trapezu ABCD mają odpowiednio długości:
AB  10 cm i
ACB= 90
AC= 60
AB= 61
2.
Podstawy trapezu ABCD mają odpowiednio długości:
AB  10 cm i
CD  4 cm. Proste zawierające ramiona trapezu przecinają się w punkcie O
CD  4 cm. Proste zawierające ramiona trapezu przecinają się w punkcie
O (jak na rysunku obok), oddalonym o 9 cm od punktu A. Oblicz długość
ramienia AD tego trapezu.
(jak na rysunku obok), oddalonym o 7 cm od punktu A. Oblicz długość ramienia
AD tego trapezu.
3. Wpisz odpowiednie oznaczenia długości boków podanych trójkątów tak, aby prawidłowo określone były
następujące funkcje trygonometryczne.
3.
Wpisz odpowiednie oznaczenia długości boków podanych trójkątów tak,
aby prawidłowo określone były następujące funkcje trygonometryczne.
a)
a)
sin  = ...........................
cos  = ..............
ctg  = ..........................
tg  = ................
b)
sin  = .................
b)
cos  = ......................
ctg  = ..................
3
. Oblicz
5
tg  = ......................
4.
1
7
5.
Wyznacz pozostałe funkcje trygonometryczne kąta , wiedząc, że  jest kątem ostrym i sin  =
6.
Oblicz długość okręgu oraz pole koła, w którym środek okręgu S jest punktem o współrzędnych (2, –3) i do
Wysokość rombu ABCD ma długość 5, a sinus kąta ostrego rombu jest równy
5.
Wyznacz pozostałe funkcje trygonometryczne kąta , wiedząc, że  jest kątem ostrym i cos  =
6.
Oblicz długość okręgu oraz pole koła, w którym środek okręgu S jest punktem o współrzędnych (–3, –2) i do
okręgu należy punkt A o współrzędnych (–2,  ( 2  3 )).
7.
(*)Wykaż, że dla dowolnego kąta ostrego
 , następująca równość jest tożsamością:
 cos2  1 tg2   1  tg2 
.
Wysokość rombu ABCD ma długość 6, a sinus kąta ostrego rombu jest równy 4 . Oblicz pole tego rombu.
pole tego rombu.
4.
5
.
okręgu należy punkt A o współrzędnych (4, –(3 + 5 ))
7. (*)Wykaż, że dla dowolnego kąta ostrego  , następująca równość jest tożsamością:
 cos2  1 tg2   1  tg2 
1.
5