Wykład 4
Zmienne losowe i ich rozkłady teoretyczne
1.
Zmienna losowa jest to taka zmienna, która
.................................................................
......................... .............................................. .........................................
.....
2.
.
Wyróżnia się zmienne losowe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.1. Funkcję zmiennej . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . można zapisać w postaci:
P( X = x i ) = pi
gdzie: pi ≥ 0
(4.1)
i = 1, 2, 3, 4...
(4.2)
pi 1
i 1
a) Dystrybuanta . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
F ( X ) Px xi
(4.3)
w przypadku . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
F X pi
i=1,2,3
xi x
(4.4)
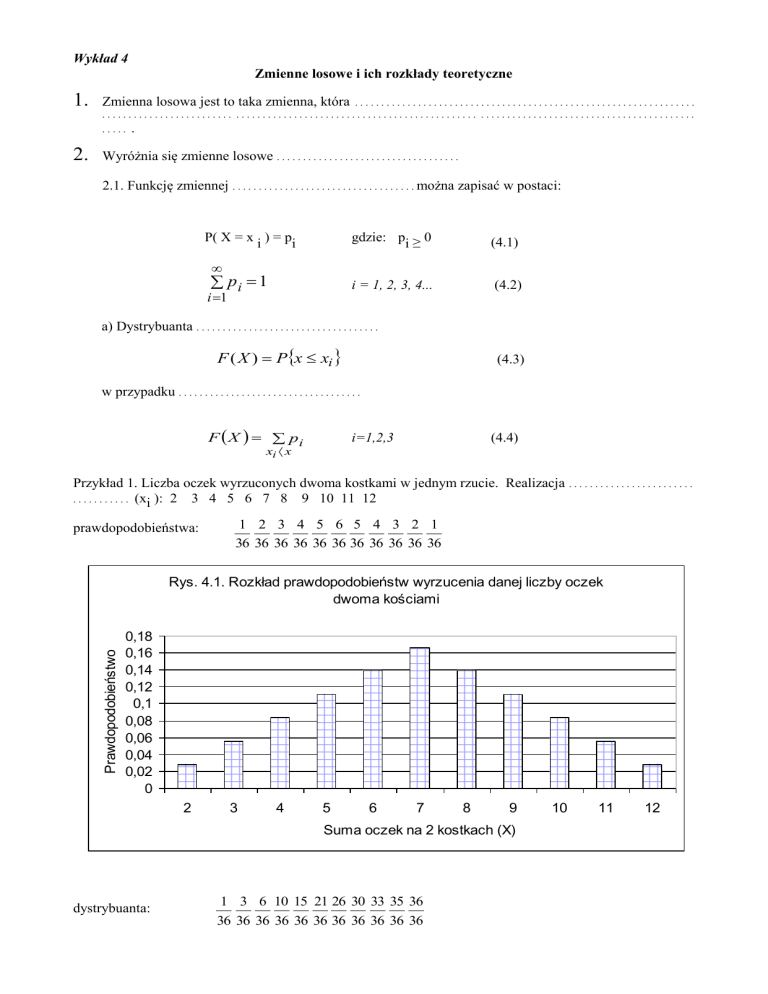
Przykład 1. Liczba oczek wyrzuconych dwoma kostkami w jednym rzucie. Realizacja . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . (xi ): 2 3 4 5 6 7 8 9 10 11 12
prawdopodobieństwa:
1 2 3 4 5 6 5 4 3 2 1
36 36 36 36 36 36 36 36 36 36 36
Prawdopodobieństwo
Rys. 4.1. Rozkład prawdopodobieństw wyrzucenia danej liczby oczek
dwoma kościami
0,18
0,16
0,14
0,12
0,1
0,08
0,06
0,04
0,02
0
2
3
4
5
6
7
8
9
Suma oczek na 2 kostkach (X)
dystrybuanta:
1 3 6 10 15 21 26 30 33 35 36
36 36 36 36 36 36 36 36 36 36 36
10
11
12
Prawdopodobieństwo
Rys. 4.2. Dystrybuanta rozkład prawdopodobieństw wyrzucenia danej
liczby oczek dwoma kościami
1
0,8
0,6
0,4
0,2
0
2
3
4
5
6
7
8
9
10
11
12
Suma oczek na 2 kostkach (X)
Znając dystrybuantę można odtworzyć rozkład i na odwrót
b) Własności . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1)
0 F x 1
x ,
dla
(4.5)
2) jest funkcją . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ., tzn. dla
x1 x2
zawsze
F x1 F x2
3) F 0,F 1
4)
P(a x b) F b F a
(4.6)
(4.7)
(4.8)
Wartość . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (nadzieja matematyczna)
n
E x xi pi
i 1
(4.9)
Własności E(x)
a) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .: E(C) = C
(4.10)
b) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .: E(x+y) = E(x) + E(y)
(4.11)
i uogólniając
E(X+Y+Z+...) = E(X)+E(Y)+E(Z)+...
(4.12)
c) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . E(XY) = E(X) E(Y)
(4.13)
d) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . E(CX) = C E(X)
(4.14)
Wariancja . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2
n
S 2 X X i E X 2 pi EX E X 2
(4.15)
i 1
lub
S 2 X E X 2 E X 2
(4.16)
odchylenie standardowe
S X S 2 X
(4.17)
Własności . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . X:
S 2 C 0
1) Wariancja stałej = 0
2) Wariancja . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .:
(4.18)
S 2 CX C 2 S 2 X
(4.19)
3) Wariancja sumy dwóch
a) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
S 2 X Y S 2 X S 2 Y
(4.20)
b) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
S 2 X Y S 2 X S 2 Y 2 cov XY
(4.21)
4) Wariancja . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
S 2 X Y S 2 X S 2 Y
(4.22)
5) Wariancja . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
S 2 X Y S 2 X S 2 Y 2 cov XY
(4.23)
gdzie cov(YX) oznacza kowariancję zmiennych X i Y:
covYX
1
X X Y Y
n
(4.24)
Wybrane rozkłady zmiennej skokowej
I. Rozkład dwumianowy (Bernouliego)
Niechaj Px oznacza prawdopodobieństwo tego, że zdarzenie A wystąpi x razy w n próbach
(niezależnych eksperymentach)
P( X x) nx p x q n x
(4.25)
n
Px 1
(4.26)
q=1–p
(4.27)
x 0
3
nx Cnx x! nn! x!
(4.28)
Rozkład dwumianowy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
............................................................... .......................................................
............................................................... .......................................................
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ..
Współczynniki (4.28) noszą nazwę współczynników dwumianowych lub liczb trójkąta Pascala
Współczynniki rozwinięcia dwumianu (p+q)n
n
n=0
1
n=2
1
n=3
1
n=4
1
n=5
1
n=6
n=8
20=1
1
n=1
n=7
Suma (liczba
konfig. 2n)
1
1
8
3
5
6
7
6
15
4
20
56
15
25=32
1
6
21
56
24=16
1
5
35
70
23=8
1
10
35
22=4
1
3
10
21
28
2
4
21=2
1
26=64
1
7
28
Suma współczynników dwumianu Newtona w każdym wierszu trójkąta Pascala =
1
8
27=128
28=256
2n.
Używając ogólnych symboli, trójkąt Pascala można także zapisać:
00
10
11
4
02
30
4
0
0n
13
14
15
50
12
22
32
34
42
52
1n
53
n
x
33
44
55
54
nn1
nn
Jeśli p=q, to z trójkąta Pascala można odczytać nie tylko liczbę kombinacji, ale łatwo obliczyć
prawdopodobieństwo osiągnięcia m zdarzeń wyróżnionych w n niezależnych próbach (eksperymentach)
n
x
P X m
n
2
(4.29)
W przypadku, gdy p q, rozkład dwumianowy jest rozkładem asymetrycznym. Dla p>0,5 jest to
asymetria lewostronna, a dla p<0,5 asymetria prawostronna, p = q - rozkład symetryczny.
Wartość . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
E X n p
(4.30)
Wariancja . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
S 2 X n p q
(4.31)
Odchylenie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
S x npq
.......
(4.32)
Rozkład dwumianowy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. r_tym . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
....
(4.33)
n
n
r
M c ( r ) X np p
x 0
x
x (1 p) n x
Można wykazać (por. G. Calot (1977 s. 107-108), że:
M c (0) = 1; M c (1) = 0
(4.34)
M c (2) = npq
(4.35)
M c (3) = npq(q - p)
(4.36)
M c (4) = npq(1 – 6pq + 3npq)
(4.37)
5
Współczynnik asymetrii
(4.38)
3
M c (3)
(q p) npq0,5
3
S
Współczynnik . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4
M c (4)
S4
3 (1 6pq) npq1
(4.39)
Modalna w rozkładzie dwumianowym . . . . . . . . . . .
..........
............................................................... .......................................................
..
Autorzy podręczników . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . .. Nie są stosowane wzory interpolacyjne na wyznaczenie „dokładnej” liczby1. Poprzestaniemy . .
................................................... ...................................................................
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .:
np – q < Mo < np + p
(4.40)
............................................................... .......................................................
............................................................... .......................................................
....................................................................... ...............................................
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ..
Przykłady zastosowań rozkładu dwumianowego:
......................................................................
......................................................................
......................................................................
......................................................................
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .,
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ..
II. Rozkład Poissona
Twórcą rozkładu jest francuski matematyk Simeon Denis Poisson (1781-1840). Niemiecki statystyk
polskiego pochodzenia W. Bortkiewicz (1868-1931) nazwał . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. Można wykazać, że . . . . . . .
......................................................................................................................
.....................................................................................
zmienna losowa X ma
rozkład Poissona:
P X x
gdzie
x
e
x!
x=0, 1, 2, ...
n p
(4.41)
(4.42)
jest . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .,
e 2,71828
1
jest podstawą logarytmów naturalnych.
Por. J. Paradysz (1990 s. 124-125).
6
E X S 2 X
(4.43)
Rozkład Poissona jest prawostronnie skośnym a wraz ze wzrostem
dąży do rozkładu symetrycznego.
Rozkład Poissona posiada dowolnego r-tego rzędu momenty centralne:
e x
X m
M c (r )
x!
x 0
r
n
(4.44)
gdzie
Mc(0) = 1; Mc (1) = 0
(4.45)
Mc(2) = λ
(4.46)
Mc(3) = λ
(4.47)
Mc(4) = λ(1 + 3*λ)
(4.48)
Współczynnik . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .:
Alfa3 = Mc(3)/S3 = λ-0,5 > 0
(4.49)
Współczynnik . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .:
Alfa4 = Mc(4)/S4 = λ-1
(4.50)
Modalna . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .:
Zakładając, że
(fMo+1/ fMo)
<1
(4.51)
oraz
(fMo-1/ fMo)
<1
(4.52)
skąd
(λ /Mo +1)
<1
(4.53)
oraz
(Mo/ λ )< 1
(4.54)
w rezultacie
λ – 1 < Mo < λ.
(4.55)
W rozkładzie Poissona . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. Gdy λ. jest równa 5, to. . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ., patrz rys. 4.3.
Przykład 2. Pewien hurtownik zamierza wprowadzić do sprzedaży nowy proszek do prania X2000.
Optymistycznie ocenia, że około 70% detalistów będzie zainteresowana tym proszkiem. Analizę rynku
powierza firmie pod nazwą Pytia Delficka, która postanowiła przebadać 20 detalistów. Ilu z nich kupi ów
proszek? Jeśli intuicja hurtownika by go nie zawiodła, to według rozkładu dwumianowego
Rys. 4.3. Rozkład Poissona dla lambdy = 5
Gęstość rozkładu
0,20
0,15
0,10
0,05
0,00
0
1
2
3
4
5
6
7
8
9
10
Realizacje zmiennej losowej
prawdopodobieństwo, że:
7
nikt nie kupi
P(X=0)=
020 0,70 0,320
0,000
1 kupi
P(X=1)=
120 0,71 0,319
0,000
6 kupi
P(x=6)=
620 0,76 0,314
0,000
7 kupi
P(X=7)=
720 0,77 0,313
0,001
8 kupi
P(X=8)=
820 0,78 0,312
0,004
9 kupi
P(X=9)=
0,012
10 kupi
P(X=10)=
0,031
11 kupi
P(X=11)=
0,065
12 kupi
P(X=12)=
0,114
13 kupi
P(X=13)=
0,164
14 kupi 70%
P(x=14)=
0,192
15 kupi
P(x=15)=
0,179
16 kupi
P(x=16)
0,130
19 kupi
P(x=19)=
0,7
20 kupi
P(x=20)=
0,7
20
19
20
20
19
20
0,31
0,30
0,007
0,001
Prawdopodobieństwo, że kupi 15 i więcej = =P(X=15)+P(X=16)+...+P(X=20) = 0,179+0,130+.....+0,001=0,417
W istocie rzeczy, jak . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Przyczyną mogło być:
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ..
a) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
b) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
..............................................................
Aproksymacja rozkładu dwumianowego rozkładem Poissona
Zakłada się, że zmienia się tylko liczebność próby a prawdopodobieństwo sukcesu jest wszędzie takie same
(p=0,02).
n=50 p=0,02
n=100 p=0,02
n=200 p=0,02
x
dwumianowy
=1
dwumianowy
=2
dwumianowy
=4
8
0
0,364
0,368
0,133
0,135
0,018
0,018
1
0,372
0,368
0,271
0,271
0,072
0,073
2
0,186
0,184
0,273
0,271
0,146
0,147
3
0,061
0,061
0,182
0,180
0,196
0,195
4
0,015
0,015
0,090
0,090
0,197
0,195
5
0,003
0,003
0,035
0,036
0,158
0,156
6
0,000
0,001
0,011
0,012
0,105
0,104
7
0,000
0,000
0,003
0,003
0,059
0,060
8
0,000
0,000
0,001
0,001
0,029
0,030
9
0,000
0,000
0,000
0,000
0,013
0,013
10
0,000
0,000
0,000
0,000
0,005
0,005
Rys. 4.4. Porównanie rozkładów prawdopodobieństw
dwumianowego i Poissona (n=100; p=0,02; lambda=2)
Prawdopodobieństwo
0,3
0,25
0,2
0,15
Rozkład Poissona
0,1
0,05
0
0
1
2
3
4
5
6
7
8
9
10
Realizacje zmiennej losowej X
Przykład 3. Dom handlowy, . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . .. W przypadku długopisów w . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
......................................................................................................................
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .?
Rozwiązanie: p = 0,02; n = 50;
np=1;
zgodnie z rozkładem Poissona (patrz powyższa tablica):
P(x=3) = 0,061
P(x=4) = 0,015
P(x=5) = 0,003
P(x=6) = 0,001
Razem 0,080 Prawdopodobieństwo tego, że więcej niż 2 długopisy nie będą pisać wynosi 0,08.
Przykłady zastosowań rozkładu Poissona:. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
.. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . .
......................................................................................................................
.................................................... ..................................................................
..........................
9
III. Rozkład hipergeometryczny
Rozkład hipergeometryczny . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
......................................................................................................................
......................................................................................................................
......................................................................................................................
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ..
Niechaj X oznacza . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
......................................................................................................................
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ..
Na
N składa się N1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . i N2, . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Prawdopodobieństwo osiągnięcia
N1 N 2
x
n x
P( X x)
N
n
dla x = 0, 1, 2, ..., min(n, N1) (4.56)
gdzie: N – liczebność całej populacji,
N1 – . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
N2 – . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
n -......................................................................
x -......................................................................
n-x - . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
min(n, N1) – . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Przykład 4. Prawdopodobieństwo „odgadnięcia” właściwych liczb w totolotku, gdzie 49 liczb stanowi
populację generalną a próbę 6 wylosowanych liczb:
6 43
wylosowanie „piątki”:
5
1
P ( X 5) 0,00001845 ,
49
6
wylosowanie „szóstki”:
6 43
6
0
0,0000000715 .
P ( X 6)
49
6
Parametry rozkładu hipergeometrycznego:
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .:
E(X) = n*N1/N
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .:
N
N n N1
S x2
1 1
n
N
1
N
N
(4.57)
(4.58)
Przykład 5. Populacja generalna zawiera 500 samochodów, z czego 50 jest z wadami trudnymi do wykrycia
przy zakupie. Kupując partię 10 samochodów:
a) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
b) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
c) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
10
