Transformaty funkcji okresowych
Niech f(t) – funkcja okresowa o okresie T o postaci:
f (t ) = f T (t ) ⋅ ∏ (t ) + f T (t − T ) ⋅ ∏ (t − T ) + f T (t − 2T ) ⋅ ∏ (t − 2T ) + K
T
T
T
∞
f (t ) = ∑ f T (t − kT ) ⋅ ∏ (t − kT )
k =0
T
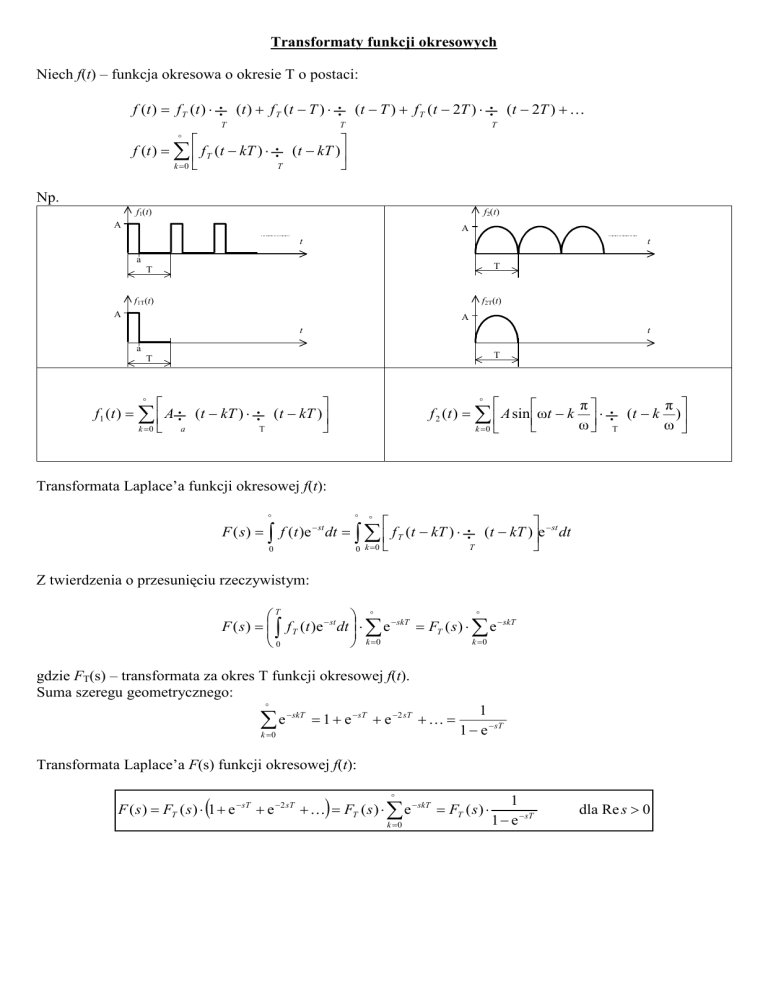
Np.
f1(t)
f2(t)
A
A
t
t
a
T
T
f1T(t)
f2T(t)
A
A
t
t
a
T
T
∞
f 1 (t ) = ∑ A∏ (t − kT ) ⋅ ∏ (t − kT )
k =0
a
T
∞
π
π
f 2 (t ) = ∑ A sin ωt − k ⋅ ∏ (t − k )
ω T
ω
k =0
Transformata Laplace’a funkcji okresowej f(t):
∞
∞
∞
F ( s ) = ∫ f (t )e − st dt = ∫ ∑ f T (t − kT ) ⋅ ∏ (t − kT )e −st dt
T
0
0 k =0
Z twierdzenia o przesunięciu rzeczywistym:
∞
T
∞
F ( s ) = ∫ f T (t )e − st dt ⋅ ∑ e − skT = FT ( s ) ⋅ ∑ e − skT
k =0
0
k =0
gdzie FT(s) – transformata za okres T funkcji okresowej f(t).
Suma szeregu geometrycznego:
∞
∑e
− skT
= 1 + e − sT + e −2 sT + K =
k =0
1
1 − e − sT
Transformata Laplace’a F(s) funkcji okresowej f(t):
F ( s ) = FT ( s ) ⋅ (1 + e − sT + e − 2 sT + K) = FT ( s ) ⋅ ∑ e − skT = FT ( s ) ⋅
∞
k =0
1
1 − e − sT
dla Re s > 0
Przykład 1. Znaleźć L-transformatę funkcji okresowej f1(t) (patrz rysunek).
•
1− e
1 1
f 1T (t ) = A[1(t ) − 1(t − a )] = A − e − sa = A
s
s s
− sa
− sa
1− e
1
1− e
F1 ( s ) = A
=A
− sT
s 1− e
s (1 − e − sT )
− sa
= F1T ( s )
Przykład 2. Znaleźć L-transformatę funkcji okresowej f2(t) (patrz rysunek).
π 1
Okres funkcji f2(t): T = = Tsin
ω 2
π
−s
π •
ω
ω
f T (t ) = A sin[ωt ] ⋅ ∏ (t ) = A sin (ωt ) ⋅ 1(t ) − 1(t − ) = A 2
1
+
e
ω
s + ω 2
T
−s
1
F2 ( s ) = F2T ( s )
1− e
−s
π
ω
π
ω 1+ e ω
=A 2
π
−s
s + ω2
1− e ω
Przykład 3. Znaleźć L-transformatę funkcji okresowej f(t) pokazanej na rysunku.
f(t)
fT(t)
A
A
t
t
T
T
• A 1 − e − sT
A
e − sT A 1 − (1 + sT )e − sT
t [1(t ) − 1(t − T )] =
−
T
= ⋅
= FT ( s )
T
T s2
s T
s2
FT (t )
A 1
e − sT
F (t ) =
=
−T
1 − e − sT T s 2
s (1 − e − sT )
f T (t ) =
Przykład 4. Znaleźć L-transformatę funkcji okresowej f(t) pokazanej na rysunku.
f (t)
fT (t)
A
A
t
t
T
Okres funkcji f(t): T =
T
2π
= Tsin
ω
π
−s
π •
ω
ω
f T (t ) = A sin[ωt ] ⋅ ∏ (t ) = A sin (ωt ) ⋅ 1(t ) − 1(t − ) = A 2
1 + e = FT ( s )
ω
s + ω 2
2π
ω
F ( s ) = FT ( s )
−s
1
1− e
−s
2π
ω
π
ω
π
2π
2π
−s
−s
−s 2
ω
1+ e
ω
ω
ω
=A 2
=A 2
1 + e ⋅ 1 + e
+ e ω + K
2π
2
2
−s
s +ω
s +ω
1 − e ω 144424443 1444
424444
3
FT ( s )
przesuni ęcia f T ( t ) w dziedzinie t
2π
2π
2π
2π
−s
−s 2
−s
−s 2
ω
ω
ω
F ( s ) = FT ( s ) ⋅ 1 + e
+e
+ K = FT ( s ) + FT ( s ) ⋅ e
+ F ( s) ⋅ e ω + K
123 14243 1T 42
4 43
4
←→
•
•
•
←→
f T ( t −T )
←→
f T ( t −2T )
fT ( t )
Przykład 5. W obwodzie SLS, o schemacie pokazanym na rysunku, obliczyć czasowy przebieg prądu i(t).
e(t)
i(t)
A
e(t)
t
C
a
T
Rozwiązanie
Transformata napięcia wymuszającego:
•
1 − e − sa
1
1 − e − sa
(
e(t ) = E ( s ) = A
=
A
1 + e −sT + e −2 sT + e −3sT + K)
− sT
s 1− e
s
Prąd:
1 − e − sa
1
I ( s ) = Y ( s ) E ( s ) = Cs ⋅ A
= A ⋅ C (1 − e −sa )(1 + e − sT + e −2 sT + e −3sT + K)
s 1 − e −sT
I ( s ) = A C ⋅ (1 − e − sa ) + A C ⋅ (1 − e − sa )e − sT + A C ⋅ (1 − e − sa )e −2 sT + A C ⋅ (1 − e − sa )e −3sT + K
14
4244
3 144
42444
3 144
42444
3 144424443
↔ i(t)
↔ i ( t −T )
↔ i ( t −2T )
↔ i ( t −3T )
i (t ) = AC [δ (t ) − δ (t − a )] + AC [δ (t − T ) − δ [t − (a + T )]] + AC [δ (t − 2T ) − δ [t − (a + 2T )]] + K
∞
i (t ) = AC ∑ [δ (t − kT ) − δ [t − (a + kT )]]
k =0
i(t)
t
a
T
T
T
Przykład 6. W obwodzie SLS, o schemacie pokazanym na rysunku, obliczyć czasowy przebieg prądu i(t).
e(t)
i(t)
A
e(t)
C
t
T
A 1
e − sT
E ( s) = 2 − T
T s
s (1 − e − sT )
I ( s) =
i(t ) =
AC 1
e − sT
− T
T s
1 − e − sT
AC 1
=
− AC (e − sT + e −2 sT + e −3sT + e −4 sT + K)
T
s
∞
AC
1(t ) − AC ∑ δ (t − kT )
T
k =1
i(t)
AC
T
t
T
T
T
Przykład 6. W obwodzie SLS, o schemacie pokazanym na rysunku, obliczyć czasowy przebieg prądu i(t).
e(t)
i(t)
A
e(t)
C
t
R
T
E ( s) =
e − sT A 1
1
A 1
= 2 − T (e − sT + e −2 sT + e −3sT + K)
−
T
2
− sT
T s
s (1 − e ) T s
s
1
A s 1
⋅ 2 − T (e −sT + e −2 sT + e −3sT + K)
1
RT s + s
s
τ
1
A
A 1
I ( s) =
−
⋅ (e − sT + e −2 sT + e −3sT + K)
gdzie
1
1 R
RT
s+
s s +
τ
τ
I ( s) = Y ( s) E ( s) =
τ = RC
t
t − kT
−
Aτ
A ∞ − τ
τ
i(t ) =
(1 − e ) ⋅ 1(t ) − ∑ e
⋅ 1(t − kT )
RT
R k =1
Dla R=1 Ω, C=1 F, A=1 V, T= 1 s oraz k= 1, 2, 3 ( bardzo duŜe uproszczenie, bo k→∞ ☺ )
1
1
0.75
0.5
0.5
0.25
2
4
6
8
10
2
-0.5
-0.25
-1
-0.5
4
6
8
10
Przykład 7. W obwodzie SLS, o schemacie pokazanym na rysunku, obliczyć czasowe przebiegi f. obwodowych
e (t)
R
A
e(t)
C
u(t)
t
T
i(t)
N
2 π 2 π 2 π π
e(t ) = A∑ sin ω t −
k ⋅ 1 t −
k − 1 t −
k−
ω
ω
ω ω
k =0
ω
E ( s) = A 2
s + ω2
π
−s
−s N
1 + e ω ⋅ ∑ e ω
k =0
2π
k
1
Cs
A 1
ω
⋅ 2
U ( s) =
E ( s) = ⋅
1
1 s + ω2
τ
R+
s+
Cs
τ
A
u (t ) =
1 + τ 2ω 2
Aτ ω
+
1 + τ 2ω 2
π
2π
2π
−s
−s
−s 2
ω
ω
⋅ 1 + e ⋅ 1 + e
+ e ω + K
N
2π π
k − 1t − (2k + 1) +
ω ω
∑ [sin(ωt − 2πk ) − τ ω cos(ωt − 2πk )]⋅ 1 t −
k =0
N
∑e
−
1
2π
k
t −
τ
ω
k =0
i (t ) = G[e(t ) − u(t )]
2π τ πω π
k − e 1t − (2k + 1)
⋅ 1 t −
ω
ω
A= 10 V, ω= 2π (T= 1 s),τ= RC= 0,5 s,
N= 5 – sześć impulsów napięcia e(t)
A= 10 V, ω= 2π (T= 1 s),τ= RC= 0,5 s,
N= 0 – jeden impuls napięcia e(t)
10
10
8
8
6
6
4
4
2
2
0.5
1
A= 10 V, ω= 2π (T= 1 s),τ= RC= 5 s,
N= 0 – jeden impuls napięcia e(t)
1.5
2
1
10
10
8
8
6
6
4
4
2
2
0.5
1
1.5
2
2
3
4
5
6
7
A= 10 V, ω= 2π (T= 1 s),τ= RC= 0,5 s,
N= 5 – sześć impulsów napięcia e(t)
1
2
3
4
5
6
7
Napięcie wymuszjace, napięcie na pojemności oraz prąd w obwodzie
A= 10 V, ω= 2π (T= 1 s),τ= RC= 0,5 s, R= 2 Ω, N= 2 – trzy impulsy napięcia e(t)
12
10
eHtL,uHtL,iHtL
8
6
4
2
0
-2
0
1
2
t@sD
3
4
MOCE chwilowe źródła, rezystora oraz kondensatora
A= 10 V, ω= 2π (T= 1 s),τ= RC= 0,5 s, R= 2 Ω, N= 3 – cztery impulsy napięcia e(t)
p e ( t ) = e( t ) ⋅ i ( t ) = e( t ) ⋅
e( t ) − u ( t )
R
[e(t ) − u(t )] 2
e( t ) − u ( t )
p R (t ) = R ⋅ i 2 (t ) = R ⋅
=
R
R
2
[W]
40
40
30
30
pR HtL @WD
peHtL@WD
[W]
20
10
20
10
0
0
0
1
2
3
4
5
t@ sD
p e ( t ) = p R ( t ) + p C ( t ) = e( t ) ⋅
0
1
2
3
4
5
t@sD
e( t ) − u ( t )
R
pC (t ) = u (t ) ⋅ i (t ) = u (t ) ⋅
[W]
e(t ) − u (t )
R
[W]
10
30
pCHtL @WD
peHtL=pRHtL+ pCHtL @WD
40
20
10
5
0
-5
-10
0
0
1
2
3
t@sD
4
5
0
1
2
3
t@sD
4
5
Energie chwilowe źródła, rezystora oraz kondensatora
A= 10 V, ω= 2π (T= 1 s),τ= RC= 0,5 s, R= 2 Ω, N= 3 – cztery impulsy napięcia e(t)
t
70
we (t ) = ∫ pe ( x )dx
60
0
wR HtL @JD
50
t
wR (t ) = ∫ p R ( x )dx
0
40
30
20
10
t
wC (t ) = ∫ pC ( x )dx
0
0
0
1
2
3
4
5
t@sD
40
100
30
80
wC HtL @JD
weHtL @JD
20
60
40
20
10
0
-10
-20
0
-30
0
1
2
3
t@ sD
4
5
0
1
2
3
t@ sD
4
5
Przykład 8. W obwodzie SLS o schemacie pokazanym na rysunku obliczyć czasowe przebiegi f. obwodowych.
e (t)
R
A
e(t)
L
u(t)
t
T
i(t)
N
2 π 2 π 2 π π
e(t ) = A∑ sin ω t − k ⋅ 1 t − k − 1 t − k −
ω
ω
ω ω
k =0
ω
E ( s) = A 2
s + ω2
U ( s) =
π
−s
−s N
1 + e ω ⋅ ∑ e ω
k =0
2π
k
ω
Ls
s
E ( s) = A ⋅
⋅ 2
1 s + ω2
R + Ls
s+
τ
π
2π
2π
−s
−s
−s 2
⋅ 1 + e ω ⋅ 1 + e ω + e ω + K
Aτω N
[cos(ωt − k 2π ) + τ ω sin(ωt − k 2π )]⋅ 1 t − k 2π − 1 t − 2k + 1 π +
u (t ) =
2 2 ∑
1 + τ ω k =0
ω
ω
π
2π τω 2k + 1 − τ t − k ω
Aτω N
−
∑ 1 t − k ω + e 1 t − ω π ⋅ e
1 + τ 2ω 2 k = 0
1
2π
A= 10 V, ω= 2π (T= 1 s),τ= GL= 0,5 s, R= 1 Ω, N= 4 – pięć impulsów napięcia e(t)
eHtL,uHtL,iHtL
10
7.5
5
2.5
0
-2.5
0
1
2
3
t@sD
4
5
6
Przykład 9 W obwodzie SLS o schemacie pokazanym na rysunku obliczyć czasowe przebiegi f.
obwodowych.
e(t)
R
A
e(t)
L
t
u(t)
a
T
N
e(t ) = A∑[1(t − kT ) − 1(t − a − kT )]
k =0
1 1
E ( s ) = A − e − sa ⋅ (1 + e − sT + e − s 2T + K)
s s
Ls
1 − e − sa
U ( s) =
E ( s) = A
⋅ (1 + e − sT + e − s 2T + K)
1
R + Ls
s+
τ
a
− t −τkT
τ
u (t ) = A ⋅ ∑ 1(t − kT ) − e 1(t − a − kT ) ⋅ e
k =0
N
t −kT
t −a −kT
−
−
A N
τ
τ
(
)
(
)
i (t ) = G ⋅ [e(t ) − u (t )] = ⋅ ∑ 1 − e
1
t
kT
1
e
1
t
a
kT
⋅
−
−
−
⋅
−
−
R k =0
A= 5 V, T= 1 s, a= 0,5 T, τ= GL= 0,2 s, R= 1 Ω, N= 4 – pięć impulsów napięcia e(t)
6
eHtL @VD
4
2
0
-2
-4
0
1
2
t@sD
6
4
6
4
4
2
iHtL @AD
uHtL @VD
3
0
-2
-4
2
0
-2
-4
0
1
2
t@sD
3
4
0
1
2
t@sD
3
4
Przykład 10 W obwodzie SLS o schemacie pokazanym na rysunku obliczyć czasowe przebiegi f. obwodowych.
e(t)
R
A
e(t)
t
u(t)
C
a
T
N
e(t ) = A∑ [1(t − kT ) − 1(t − a − kT )]
k =0
1 − e − sa
⋅ (1 + e − sT + e − s 2T + K)
s
1
A 1 − e − sa
⋅ (1 + e − sT + e − s 2T + K)
U ( s ) = Cs E ( s ) = ⋅
1
1
τ
R+
s s +
Cs
τ
E ( s) = A
t −kT
t − a −kT
N
−
−
u (t ) = A ⋅ ∑ 1 − e τ ⋅ 1(t − kT ) − 1 − e τ ⋅ 1(t − a − kT )
k =0
a
− t −τkT
τ
i (t ) = A ⋅ ∑ 1(t − kT ) − e 1(t − a − kT ) ⋅ e
k =0
N
A= 5 V, T= 1 s, a= 0,5 T, τ= RC= 0,2 s, R= 1 Ω, N= 4 – pięć impulsów napięcia e(t)
6
eHtL @VD
4
2
0
-2
-4
1
2
t@sD
6
6
4
4
2
2
iHtL @AD
uHtL @VD
0
0
-2
3
4
0
1
0
-2
-4
-4
0
1
2
t@sD
3
4
Wyniki przykładu 10 porównać z wynikami przykładu 9 – przemyśleć i zapamiętać ☺ !
2
t@ sD
3
4
Przykład 11 W obwodzie SLS o schemacie pokazanym na rysunku obliczyć strumień ϕ(t) w elemencie L.
e(t)
R
A
e(t)
L
u(t)
t
T
e(t ) =
A N
∑ (t − kT )[1(t − kT ) − 1[t − (1 + k )T ]]
T k =0
E ( s) =
A 1 − (1 + sT )e − sT
⋅
⋅ (1 + e − sT + e − s 2T + K)
2
T
s
E ( s)
A 1 − (1 + sT )e − sT
= ⋅
⋅ (1 + e − sT + e − s 2T + K)
1
R + Ls T
s2 s +
τ
t − kT
t −( k +1) T
−
−
τ N
τ
ϕ (t ) = A ⋅ ∑ t − kT − τ 1 − e τ ⋅ 1(t − kT ) − t − ( k + 1)T + (T − τ)1 − e
T
k =0
Φ( s) = L ⋅ I ( s) = L
⋅ 1[t − ( k + 1)T ]
10
1
8
0.8
φHtL @WbD
eHtL @VD
A= 10 V, T= 1 s, τ= GL= 0,1 s, N= 3 – cztery impulsy napięcia e(t)
6
4
0.6
0.4
2
0.2
0
0
0
1
2
t@sD
3
4
0
1
2
t@ sD
3
4
Impuls bramkowy prostokątny
∏(t; τ)
1
∏ (t; τ ) = 1(t ) − 1(t − τ ) ;
t
τ
Wymuszenie napięciowe:
e(t)
e(t ) = A ⋅ sin ωt
A
t
, gdzie pulsacja
ω=
2π
T
.
T
1). Wymuszenie e(t) opisane jako powielony pierwszy półokres funkcji sinus
2π
T
T T
e(t ) = A ⋅ ∑ sin t − k ⋅ ∏ t − k ;
2
2 2
k =0
T
∞
k= 2
6
4
k= 0
6
2
4
0
2
-2
0
-4
-2
0
2
4
6
8
10
0
2
4
6
8
10
k= 3
-4
6
0
2
4
6
8
10
4
k= 1
6
2
4
0
2
-2
0
-4
-2
-4
0
2
4
6
8
…
…
…
10
Pierwszy okres wymuszenia:
e1(t)
A
t
T
2
2π
T
e1 (t ) = A sin t ⋅ ∏ t; =
T
2
2π T
T
2π
T
2π
= A sin t ⋅ 1(t ) − 1 t − = A sin t ⋅ 1(t ) − A sin t − + π ⋅ 1 t − =
T
2
T
T 2
2
2π T T
2π
= A sin t ⋅ 1(t ) + A sin t − ⋅ 1 t −
T
T 2 2
Transformata jednostronna Laplace’a wymuszenia wymuszenia e(t)za pierwszy okres:
2π
T
E1 ( s ) = A 2
2π
s2 +
T
T
−s
ω
⋅ 1 + e 2 = A 2
s + ω2
T
−s
⋅ 1 + e 2
2). Wymuszenie e(t) opisane jako powielone dwa pierwsze półokresy
T
2π ∞
1 + 2k T k= 62
e(t ) = A sin t ⋅ ∑ ∏ t − kT ; −∏ t −
T ;
2
2
2
T k =0
4
k= 0
2
6
0
4
-2
2
-4
0
-2
0
2
4
6
8
10
0
2
4
6
8
10
k= 3
-4
6
0
2
4
6
8
4
10
k= 1
6
2
4
0
2
-2
0
-4
-2
-4
…
…
0
2
4
6
8
10
Pierwszy okres wymuszenia e(t)
2π T
1 T
e2 (t ) = A sin t ⋅ ∏ t; −∏ t − T ; =
T 2
2 2
e2(t)
A
2π
T
= A sin t ⋅ 1(t ) − 2 ⋅ 1 t − + 1(t − T ) =
2
T
t
T
2
2π T T
2π
2π
= A sin t ⋅ 1(t ) + 2 ⋅ A sin t − ⋅ 1 t − + A sin (t − T ) ⋅ 1(t − T )
2
2
T
T
T
T
Transformata jednostronna Laplace’a wymuszenia e2{t) za pierwszy okres:
2π
T
E2 ( s ) = A 2
2π
s2 +
T
T
−s
ω
⋅ 1 + 2 ⋅ e 2 + e − s T = A 2
s + ω2
T
−s
⋅ 1 + 2 ⋅ e 2 + e − s T
Inny sposób wyznaczenia transformaty E2(s)
tw. „O liniowości transformaty Laplace’a” oraz „O przesunięciu w dziedzinie czasu”
E 2 ( s ) = E1 ( s ) + E1 ( s ) ⋅ e
Czyli taj jak powyŜej ☺ !!!
−s
T
2
T
−s
ω
= E1 ( s )1 + e 2 = A 2
s + ω2
2
T
−s
ω
⋅ 1 + e 2 = A 2
s + ω2
T
−s
⋅ 1 + 2 ⋅ e 2 + e − s T
Zadanie Wyznaczyć przebieg czasowy napięcia u(t) dla dwu róŜnych sposobów (1 i 2) tworzenia e(t). Warunki
początkowe zerowe. Dane: R= 1Ω, C= 1 F, A= 10 V, T= 2 s.
R
C
e(t)
1
Cs
1
1
U ( s) =
E ( s ) = RC E ( s ) =
E ( s ),
1
1
τ s +1
R+
s+
Cs
RC
u(t)
τ = RC
1). Wymuszenie e(t) opisane jako powielony pierwszy półokres funkcji sinus
∞
E ( s ) = E1 ( s ) ⋅ ∑ e
−sk
T
2
=A
k =0
U1 ( s) =
ω
2
s + ω2
T
T
−s ∞
−sk
⋅ 1 + e 2 ⋅ ∑ e 2
k =0
T
T
−s ∞
−sk
1
ω
1
2
2
⋅
1
+
e
⋅
e
E ( s) = A 2
⋅
∑
τ s +1
s + ω 2 τ s + 1
k
=
0
14
442444
3
F (s)
− s T2 ∞ − s k T2
U1(s) = F(s) ⋅ 1+ e ⋅ ∑e
k=0
2). Wymuszenie e(t) opisane jako powielone dwa pierwsze półokresy
∞
E ( s) = E2 ( s) ⋅ ∑ e − s k T = A
k =0
ω
2
s + ω2
T
−s
∞
⋅ 1 + 2 ⋅ e 2 + e − s T ⋅ ∑ e − s k T
k =0
T
∞
−s
1
ω
1
−sT
2
U 2 ( s) =
E ( s) = A 2
⋅
⋅
1
+
2
⋅
e
+
e
⋅
e− s k T
∑
2
τ s +1
s + ω τ s + 1
4
k =0
1
442444
3
F (s)
T
∞
−s
−
s
T
U2 (s) = F (s) ⋅ 1 + 2 ⋅ e 2 + e ⋅ ∑e− s k T
k =0
Oryginał F(s) – odpowieź na wymuszenie u(t)= A sin ωt 1(t):
t
−
ω
1 •
A
τ
(
)
(
)
F ( s) = A 2
⋅
=
τωe
−
τω
cos
ω
t
+
sin
ω
t
⋅ 1( t ) = f (t )
s + ω 2 τ s + 1 1 + τ 2ω 2
4
3
2
1
0
-1
-2
-3
0
5
10
15
20
1). Odpowiedź na pierwszy okres wymuszenia e(t)
−s T
U1T (s) = F(s) ⋅ 1+ e 2 ;
−sT ∞ −sk T
U1(s) = F(s) ⋅ 1+ e 2 ⋅ ∑e 2 ,
2443 k=0
144
T π
=
2 ω
U1T ( s)
u1T (t ) =
A
1 + τ 2ω 2
t
−
τ
τωe
− τω cos(ωt ) + sin (ωt ) ⋅ 1(t ) +
π
t−
ω
−
A
π
π
π
+
τωe τ − τω cosω t − + sin ω t − ⋅ 1 t −
2 2
1+ τ ω
ω
ω
ω
t
−
A
τ
(
)
(
)
−
+
u1T (t ) =
τωe
τω
cos
ω
t
sin
ω
t
⋅ 1(t ) +
1 + τ 2ω2
π
t−
ω
−
A
π
τ
+
τωe
+ τω cos(ωt ) − sin(ωt ) ⋅ 1 t −
2 2
1+ τ ω
ω
Odpowiedź na pierwszy impuls e(t)
Odpowiedź na drugi impuls e(t)
10
10
8
8
6
6
4
4
2
2
0
0
0
2
4
6
0
8
Suma odpowiedzi na pierwszy i drugi impuls e(t)
2
4
6
8
Odpowiedź na dziesięć impulsów e(t)
10
10
8
8
6
6
4
4
2
2
0
0
0
2
4
6
8
0
2
4
6
8
10
12
Pełna odpowiedź
π
t−k
ω
−
A
π
u1 (t ) =
τωe τ − τω cos(ωt − kπ ) + sin (ωt − kπ ) ⋅ 1 t − k +
2 2 ∑
1 + τ ω k =0
ω
N
π
t − ( k + 1)
ω
−
A
⋅ 1 t − (k + 1) π
τ
(
(
)
)
(
(
)
)
+
−
t
−
+
+
t
−
+
τωe
τω
cos
ω
k
1
π
sin
ω
k
1
π
∑
1 + τ 2 ω 2 k =0
ω
N
2). Odpowiedź na pierwszy okres wymuszenia e(t)
T
∞
−s
−sT
2
U2 (s) = F (s) ⋅ 1 + 2 ⋅ e + e ⋅ ∑e− s k T ,
44244443 k =0
144
T
−s
U2T (s) = F (s) ⋅ 1 + 2 ⋅ e 2 + e− s T
U 2T ( s )
A
u 2T (t ) =
1 + τ 2ω 2
t
−
τ
(
)
(
)
−
+
τωe
τω
cos
ω
t
sin
ω
t
⋅ 1(t ) +
π
t−
ω
−
A
π
π
π
+2
τωe τ − τω cos ω t − + sin ω t − ⋅ 1 t − +
2 2
1+ τ ω
ω
ω
ω
2π
t−
ω
−
A
2π
2π
2π
τωe τ − τω cos ω t −
+
+
sin
ω
t
−
⋅
1
t
−
1 + τ 2ω 2
ω
ω
ω
A
u 2T ( t ) =
1 + τ 2ω 2
t
−
τ
τωe − τω cos(ωt ) + sin (ωt ) ⋅ 1(t ) +
π
t−
ω
−
A
π
+2
τωe τ + τω cos(ωt ) − sin (ωt ) ⋅ 1 t − +
2 2
1+ τ ω
ω
2π
t−
ω
−
A
2π
+
τωe τ − τω cos(ωt ) + sin (ωt ) ⋅ 1 t −
2 2
1+ τ ω
ω
Odpowiedź na pierwszy impuls e(t)
Odpowiedź na drugi impuls e(t)
10
10
8
8
6
6
4
4
2
2
0
0
0
2
4
6
0
8
Suma odpowiedzi na pierwszy i drugi impuls e(t)
2
4
6
8
Odpowiedź na pięć impulsów e(t)
10
10
8
8
6
6
4
4
2
2
0
0
0
2
4
6
8
0
2
4
6
8
10
12
Pełna odpowiedź
2π
t−k
ω
−
A
2
π
2
π
2π
u2 ( t ) =
τωe τ − τω cos ω t − k + sin ω t − k ⋅ 1 t − k +
2 2 ∑
1 + τ ω k =0
ω
ω
ω
N
π
t − (2 k +1)
ω
−
A
π
τ
τωe
+2
+ τω cos(ωt − k 2π ) − sin(ωt − k 2 π ) ⋅ 1t − (2k + 1) +
2 2 ∑
1 + τ ω k =0
ω
N
2π
t − ( k + 1)
ω
−
A
2π
τ
+
τωe
− τω cos(ωt − k 2 π ) + sin(ωt − k 2 π ) ⋅ 1t − ( k + 1)
2 2 ∑
1 + τ ω k =0
ω
N
Zadanie Wyznaczyć przebieg czasowy napięcia u(t) dla wymuszenia e(t). Warunki początkowe zerowe.
Dane: R= 1Ω, C= 1 F, A= 10 V, T= 1 s.
R
C
e(t)
1
Cs
1
1
U ( s) =
E ( s ) = RC E ( s ) =
E ( s ),
1
1
τ s +1
R+
s+
Cs
RC
u(t)
τ = RC
N
e(t ) = A∑ {1(t − kT ) − 1[t − (k + 1)T ]}
Wymuszenie
k =0
k= 2
k= 0
e(t)
e(t)
A
A
t
t
T
T
2T
3T
k= 1
e(t)
lim e ( t ) = A ⋅ 1 ( t ) ☺
A
N → ∞
t
T
2T
1
ET ( s ) = A (1 − e − sT )
s
eT (t ) = A ⋅ [1(t ) − 1(t − T )]
t
t −T
−
−
uT (t ) = A1 − e τ ⋅ 1(t ) − A1 − e τ
1
1
(
U T ( s) =
E ( s) = A
1 − e − sT )
τ s +1
s (τ s + 1)
Odpowiedź uT(t)
Odpowiedź na drugi umpuls u(t)
Suma odpowiedzi
10
10
10
8
8
8
6
6
6
4
4
4
2
2
2
2
4
6
8
10
2
4
6
8
2
10
Pełna odpowiedź dla N impulsów
N
N
1
(
U N ( s ) = U T ( s ) ⋅ ∑ e − sT = A
1 − e − sT ) ⋅ ∑ e − sT
k =0
s (τ s + 1)
k =0
t − kT
−
u N ( t ) = A ⋅ ∑ 1 − e τ
k =0
N
⋅ 1(t − T )
t − ( k +1)T
−
τ
⋅ 1(t − kT ) − 1 − e
t
−
lim u N (t ) = A ⋅ 1 − e τ ⋅ 1(t )
N →∞
⋅ 1[t − (k + 1)T ]
4
6
8
10
Zadanie Wyznaczyć przebieg czasowy napięcia u(t) dla wymuszenia e(t). Warunki początkowe zerowe.
Dane: R= 1Ω, C= 1 F, A= 10 V, T= 1 s.
C
U ( s) =
e(t)
R
u(t)
R
R+
1
Cs
E ( s) =
s
s+
1
RC
[
e(t)
E ( s) =
τs
E ( s ),
τ s +1
τ = RC
]
eT (t ) = A ∏ (t; a ) − ∏ (t − a; T − a ) = A[1(t ) − 2 ⋅ 1(t − a ) + 1(t − T )]
A
t
–A
1
ET ( s ) = A (1 − 2 ⋅ e − a s + e − T s )
s
a
T
U T ( s) =
1
τs
ET ( s ) = A
(1 − 2 ⋅ e − a s + e − T s ) ,
1
τ s +1
s+
τ
123
F ( s) = A
1
1
s+
τ
•
= Ae
−
t
τ
⋅ 1(t )
F (s)
uT (t ) = Ae
−
t
τ
⋅ 1(t ) − 2 Ae
−
t −a
τ
⋅ 1(t − a ) + Ae
−
t −T
τ
⋅ 1(t − T )
10
5
1
2
3
4
5
-5
-10
-15
Pełna odpowiedź dla N impulsów
t − ( a +kT )
t − (k +1)T
−
−
− t −τkT
τ
τ
u(t ) = A∑ e
⋅ 1(t − kT ) − 2e
⋅ 1[t − (a + kT )] + e
⋅ 1[t − (k + 1)T ]
k =0
N
