Działania na liczbach rzeczywistych Zaznacz, na którym rysunku

I.
Działania na liczbach rzeczywistych
1. Zaznacz, na którym rysunku przedstawiony jest zbiór rozwiązań nierówności: x  2  4.
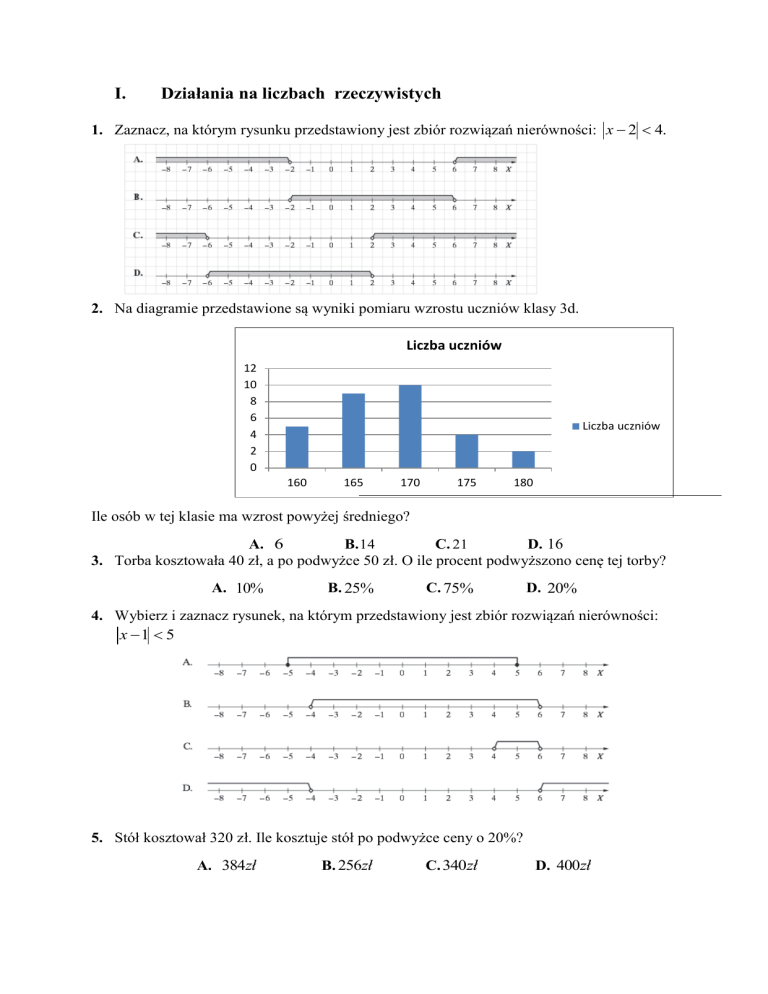
2. Na diagramie przedstawione są wyniki pomiaru wzrostu uczniów klasy 3d.
Liczba uczniów
12
10
8
6
4
2
0
Liczba uczniów
160
165
170
175
180
Ile osób w tej klasie ma wzrost powyżej średniego?
A. 6
B. 14
C. 21
D. 16
3. Torba kosztowała 40 zł, a po podwyżce 50 zł. O ile procent podwyższono cenę tej torby?
A. 10%
B. 25%
C. 75%
D. 20%
4. Wybierz i zaznacz rysunek, na którym przedstawiony jest zbiór rozwiązań nierówności:
x 1  5
5. Stół kosztował 320 zł. Ile kosztuje stół po podwyżce ceny o 20%?
A. 384zł
B. 256zł
C. 340zł
D. 400zł
6. Średnia arytmetyczna wzrostu czterech chłopców jest równa 170 cm. Chłopcy mają: 150
cm, 170 cm, 185 cm, x cm. Czwarty chłopiec mierzy:
A. 180 cm
B. 190 cm
C. 195 cm
D. 175 cm
7. Największa liczba naturalna n spełniająca nierówność: n  2  1to
A. 3
B. 5
C. 6
D. 0
8. 20% pewnej liczby jest o 16 mniejsze od tej liczby. Tą liczbą jest:
A. 32
B. 20
9. Przedział zaznaczony na osi liczbowej
C. -2
D. -20
jest zbiorem rozwiązań nierówności:
A. x  1  1
B. x  1  2
C. x  1  1
D. x  1  1
10. Mediana danych: -4; 2; 6; 0; 1 jest równa
A. 6
B. 0
C. 2,5
D. 1
11. Kwotę 10000 zł wpłacamy do banku na 4 lata. Kapitalizacja odsetek jest dokonywana w
tym banku co kwartał, a roczna stopa procentowa wynosi 3%. Po 4 latach kwotę na
rachunku będzie można opisać wzorem:
A. 10000  1,0075
12
B. 10000  1,03
4
C. 10000  1,03
16
D. 10000  1,0075
4
2
12. Liczbą przeciwną do liczby a  5 3 jest:
A. 5
3
2
B.  5
3
2
C. 5

2
3
D.  5
2
3
13. Zbiór (;8    4;) jest rozwiązaniem nierówności:
A. x  6  2
B. x  6  2
C. x  6  2
D. x  6  2
14. Wskaż nierówność, która spełniona jest przez dany przedział: x  (;2)  (6;)
A. x  2  4
B. x  2  4
C. x  4  2
D. x  4  2
15. 6% liczby x jest równe 9. Wtedy
A. x = 240
B. x =150
C. x = 24
D. x =15
16. Na seans filmowy sprzedano 280 biletów, w tym 126 ulgowych. Jaki procent sprzedanych
biletów stanowiły bilety ulgowe?
A. 22%
B. 33%
C. 45%
D. 63%
17. Średnia arytmetyczna pięciu liczb: 5, x, 1, 3, 1 jest równa 3. Wtedy
A. x = 2
B. x = 3
C. x = 4
D. x = 5
18. Wskaż rysunek, na którym jest przedstawiony zbiór rozwiązań nierówności x  7  5.
A.
B.
C.
D.
19. Spodnie po obniżce ceny o 30% kosztują 126 zł. Ile kosztowały spodnie przed obniżką?
A. 163,80 zł
B. 180 zł
C. 294 zł
D. 420 zł
20. Średnia arytmetyczna dziesięciu liczb x, 3, 1, 4, 1, 5, 1, 4, 1, 5 jest równa 3. Wtedy
A. x = 2
B. x = 3
C. x = 4
D. x = 5
21. Wskaż nierówność, którą spełnia liczba  .
A. x  1  5
B. x  1  2
C. x 
2
4
3
D. x 
1
3
3
22. Pierwsza rata, która stanowi 9% ceny roweru, jest równa 189 zł. Rower kosztuje
A. 1701 zł.
B. 2100 zł.
C. 1890 zł.
D. 2091 zł.
23. Uczniowie pewnej klasy zostali poproszeni o odpowiedź na pytanie: „Ile osób liczy twoja
rodzina?” Wyniki przedstawiono w tabeli:
Liczba osób w
rodzinie
Liczba
uczniów
3
6
4
12
x
2
Średnia liczba osób w rodzinie dla uczniów tej klasy jest równa 4. Wtedy liczba x jest
równa:
A. 3
B. 4
C. 5
D. 7
24. Cenę nart obniżono o 20%, a po miesiącu nową cenę obniżono o dalsze 30%. W wyniku
obu obniżek cena nart zmniejszyła się o
A. 44%
B. 50%
C. 56%
D. 60%
25. Wskaż liczbę, która spełnia równanie 3x  1  4 x .
A. x = -1
B. x = 1
C. x = 2
D. x = -2
26. Średnia arytmetyczna cen sześciu akcji na giełdzie jest równa 500 zł. Za pięć z tych akcji
zapłacono 2300 zł. Cena szóstej akcji jest równa
A. 400 zł
B. 500 zł
C. 600 zł
D. 700 zł
27. Liczbami spełniającymi równanie 2 x  3  5 są
A. 1 i – 4
B. 1 i 2
C. -1 i 4
D. -2 i 2
28. Marża równa 1,5% kwoty pożyczonego kapitału była równa 3000 zł. Wynika stąd, że
pożyczono:
A. 45 zł
B. 2000 zł
C. 200 000 zł
D. 450 000 zł
29. W kolejnych sześciu rzutach kostką otrzymano następujące wyniki: 6, 3, 1, 2, 5, 5.
Mediana tych wyników jest równa:
A. 3
B. 3,5
C. 4
D. 5
30. Wskaż rysunek, na którym jest przedstawiony zbiór rozwiązań nierówności x  4  7
31. Pewna firma zatrudnia 6 osób. Dyrektor zarabia 8000 zł, a pensje pozostałych
pracowników są równe: 2000 zł, 2800 zł, 3400 zł, 3600 zł, 4200 zł. Mediana zarobków
tych 6 osób jest równa
A. 3400 zł
B. 3500 zł
C. 6000 zł
D. 7000 zł
32. Wskaż rysunek, na którym zaznaczony jest zbiór wszystkich liczb rzeczywistych
spełniających nierówność x  4  5
A.
B.
C.
D.
33. Liczby a i b są dodatnie oraz 12% liczby a jest równe 15% liczby b. Stąd wynika, że a
jest równe:
A. 103% liczby b
B. 125% liczby b
C. 150% liczby b
D. 153% liczby b
34. Mediana uporządkowanego niemalejącego zestawu sześciu liczb: 1, 2, 3, x, 5, 8 jest
równa 4. Wtedy
A. x = 2
B. x = 3
C. x = 4
D. x = 5
35. Gdy od 17% liczby 21 odejmiemy 21% liczby 17, to otrzymamy
4
A. 0
B.
C. 3,57
D. 4
100
3
18
36. Suma liczby odwrotnej do liczby  4 i liczby przeciwnej do liczby
jest równa:
5
23
21
A. -1
B. 0
C. 
D. 1
23
37. Suma przedziałów  ;11  7; jest zbiorem rozwiązań nierówności:
A. x  1  10
B. x  2  9
C. x  2  11
D. x  1  10
38. Liczba a stanowi 40% liczby b. Wówczas:
A. b = 0,4a
B. b = 0,6a
C. b = 2,5a
D. b = 0,25a
39. Pan Nowak wpłacił do banku k zł na procent składany. Oprocentowanie w tym banku
wynosi 4% w skali roku, a odsetki kapitalizuje się co pół roku. Po 6 latach oszczędzania
Pan Nowak zgromadzi na koncie kwotę:
A. k 1  0,02 zł
12
B. k 1  0,04 zł
12
C. k 1  0,02 zł
6
D. k 1  0,4 zł
6
40. Liczba 5  7   3  4 jest równa:
A. -3
B. -5
C. 1
D. 3
41. Wskaż rysunek, na którym jest przedstawiony zbiór rozwiązań nierówności: x  2  3
42. Samochód kosztował 30000zł. Jego cenę obniżono o 10% , a następnie cenę po tej
obniżce ponownie obniżono o 10 %. Po tych obniżkach samochód kosztował:
A. 24400 zł
B. 24700 zł
C. 24000 zł
D. 24300 zł
43. W czterech rzutach sześcienną kostką do gry otrzymano następujące liczby oczek: 6; 3; 1;
4. Mediana tych danych jest równa
A. 2
B.
2,5
C. 5
D. 3,5
44. Cena spodni była równa 200zł. Obniżono tę cenę o 12%, a następnie podwyższono o 12%.
Po tych operacjach cena spodni była równa:
A. 200 zł
B. 176 zł
C. 224,21 zł
D. 197,12 zł
45. Wskaż nierówność, której ilustracją jest przedział:
A. 2 x  6  5
B. x  3  2,5
C. 2 x  6  5
D. x  3  3
46. Dla której z przedstawionych serii danych mediana jest równa 3?
A. 1; 1; 2; 3; 4; 7; 7; 12
C.
xt 1
ni 2
2
3
3 4
5 5
5
3
B. 1; 9; 5; 3; 3; 2; 7; 8; 9
D.
6
2
47. Jeżeli liczba 78 jest o 50% większa od liczby c, to
A. c = 60
B. c = 52
C. c = 48
48. Dla każdej liczby x, spełniającej warunek: -3 < x < 0, wyrażenie:
A. 2
B. 3
D. c = 39
|𝑥+3|−𝑥+3
6
C. − 𝑥
𝑥
jest równe:
D.
6
𝑥
49. Mediana zestawu danych: 2; 12; a; 10; 5; 3 jest równa 7. Wówczas
A. a = 4
B. a = 6
C. a = 7
D. a = 9
50. Liczba 15 jest przybliżeniem z niedomiarem liczby x. Błąd bezwzględny tego przybliżenia
jest równy 0,24. Liczba x to:
A. 14,76
B. 14,80
C. 15,20
D. 15,24
51. W klasie jest cztery razy więcej chłopców niż dziewcząt. Ile procent wszystkich uczniów
tej klasy stanowią dziewczęta?
A. 4%
B. 5%
C. 20%
D. 25%
C. 6
D. 7
52. Reszta z dzielenia liczby 55 przez 8 jest równa
A. 4
B. 5
53. Dodatnia liczba x stanowi 70% liczby y. Wówczas
A. y 
13
x
10
B. y 
7
x
10
C. y 
10
x
7
D. y 
10
x
13
54. Przedział <-1; 3> jest opisany nierównością:
A. x  1  2
B. x  1  2
C. x  1  2
D. x  1  2
55. Wyniki sprawdzianu z matematyki są przedstawione na poniższym diagramie.
Średnia ocen uzyskanych przez uczniów z tego sprawdzianu jest równa
A. 2
B. 3
C. 3,5
D. 4
56. Wskaż nierówność, która opisuje przedział zaznaczony na osi liczbowej.
A. x  7  15
B. x  7  15
C. x  15  7
D. x  15  7
57. Julia połowę swoich oszczędności przeznaczyła na prezent dla Maćka. 10% tego, co jej
zostało, przeznaczyła na prezent dla Dominiki. Ile procent oszczędności pozostało Julii?
A. 25
B. 40
C. 45
D. 55
58. Średnia arytmetyczna liczb: x, 13, 7, 5, 5, 3, 2, 11 jest równa 7. Mediana tego zestawu
liczb jest równa
A. 6
B. 7
C. 10
D. 5
59. Rozwiązaniem nierówności x  4  2 jest zbiór:
A.  ;6   2;
B.  ;6  2;
C.  6;2
D.  6;2
2
60. Liczbą odwrotną do liczby 7 3 jest
3
3
A. 7 2
B.  7 2
C. 7

3
2
D. 7

2
3
61. Wartość liczby: a  1,7  3 jest równa
A. 1,7  3
B. 1,7  3
C.  1,7  3
D.  1,7  3
62. Jeśli cenę towaru obniżono najpierw o 10%, a potem o 15%, to znaczy, że po dwóch
obniżkach cena końcowa jest obniżona w stosunku do początkowej o:
A. 23,5%
B. 25%
C. 25,5%
D. 26%
63. Cena towaru została podwyższona o 30%, a po pewnym czasie nową, wyższą cenę
ponownie podwyższono, tym razem o 10%. W rezultacie obu podwyżek wyjściowa cena
towaru zwiększyła się o:
A. 15%
B. 20%
C. 40%
D. 43%
2
przybliżymy z dokładnością do dwóch miejsc po przecinku, to błąd
3
względny tego przybliżenia jest równy:
64. Jeżeli liczbę
A.
1
%
2
B. 1%
65. Liczba 0,6 jest jednym z przybliżeń liczby
C.
1
%
3
D.
2
%
3
5
. Błąd względny tego przybliżenia,
8
wyrażony w procentach, jest równy
A. 0,025%
B. 2,5%
66. Liczba przeciwna do liczby 10
A. 10

5

3
5
3
C. 0,04%
D. 4%
to liczba:
5
C.  10
B. 10 3

3
5
D.  10

5
3
67. Zbiorem wszystkich rozwiązań nierówności 3x  6  6 jest
B.  4;0
A.  ;4  0;
C.  ;0  4;
D. 0;4
68. Ekipa złożona z 25 pracowników wymieniła tory kolejowe na pewnym odcinku w ciągu
156 dni. Jeśli wymianę torów kolejowych na kolejnym odcinku o tej samej długości
trzeba przeprowadzić w ciągu 100 dni, to, przy założeniu takiej samej wydajności, należy
zatrudnić do pracy o
A. 14 osób więcej
B. 17 osób więcej
C. 25 osób więcej
D. 39 osób więcej
69. Średnia arytmetyczna zestawu danych: 3, 8, 3, 11, 3, 10, 3, x jest równa 6. Mediana tego
zestawu jest równa
A. 5
B. 6
C. 7
D. 8
2
3
70. Liczbą odwrotną do liczby 7 jest
3
3
B. 7 2
B.  7 2
C. 7

3
2
D. 7

2
3
71. Cena pewnego towaru wraz z 7-procentowym podatkiem VAT jest równa 34 347 zł.
Cena tego samego towaru wraz z 23-procentowym podatkiem VAT będzie równa
A. 37 236 zł
B. 39 842,52 zł
C. 39 483 zł
D. 42 246,81 zł
72. Najmniejszą liczbą całkowitą dodatnią spełniającą nierówność x  4,5  6 jest
A. x = 1
B. x = 2
C. x = 3
D. x = 6
73. Wskaż rysunek, na którym przedstawiono przedział, będący zbiorem wszystkich
rozwiązań nierówności:  4  x  1  4
74. Kwotę 1000 zł ulokowano w banku na roczną lokatę oprocentowaną w wysokości 4%
w stosunku rocznym. Po zakończeniu lokaty od naliczonych odsetek odprowadzany jest
podatek w wysokości 19%. Maksymalna kwota, jaką po upływie roku będzie można
wypłacić z banku, jest równa
19
4 
81 4 


A. 1000  1 
B. 1000  1 




 100 100 
 100 100 
81 4 
19
4 


C. 1000  1 
D. 1000  1 




 100 100 
 100 100 
75. Przy 23-procentowej stawce podatku VAT cena brutto samochodu jest równa 45 018 zł.
Jaka jest cena netto tego samochodu?
A. 34663,86 zł
B. 36600zł
76. Liczba 0,3 jest jednym z przybliżeń liczby
C. 44995zł
D. 55372,14 zł
5
. Błąd względny tego przybliżenia,
16
wyrażony w procentach, jest równy
A. 4%
B. 0,04%
C. 2,5%
D. 0,025%
77. Średnia arytmetyczna zestawu danych: 2, 4, 7, 8, x jest równa n, natomiast średnia
arytmetyczna zestawu danych: 2, 4, 7, 8, x, 2x jest równa 2n. Wynika stąd, że
A. x  49
78. Jeśli a 
B. x  21
C. x  14
D. x  7
3
a b
i b  2 , to wartość wyrażenia
jest równa
2
ab
A.
2
3
B. 1
C.
6
7
D.
27
6
79. Dany jest prostokąt o wymiarach 40cm x 100cm. Jeżeli każdy z dłuższych boków tego
prostokąta wydłużymy o 20%, a każdy z krótszych doków skrócimy o 20%, to w wyniku
obu przekształceń pole tego prostokąta
A. zwiększy się o 8%
B. zwiększy się o 4%
D. zmniejszy się o 4%
C. zmniejszy się o 8%
80. Na lokacie złożono 1000 zł przy rocznej stopie procentowej p% (procent składany).
Odsetki naliczane są co kwartał. Po upływie roku wielkość kapitału na lokacie będzie
równa
4p 
A. 10001 

 100 
p 

B. 10001 

 100 
4
p 
C. 10001 

400 

p 

D. 10001 

 400 
4
81. Wykonano pomiary wysokości czterech krzeseł i każde dwa rezultaty były różne. Adam
zapisał wyniki w metrach i odchylenie standardowe jego danych było równe  A . Bogdan
zapisał te wyniki w centymetrach i odchylenie standardowe jego danych było równe  B .
Wynika stąd, że
A.  A  10 B
C. 10 A   B
B.  A  100 B
D. 100 A   B
82. Rzucono 100 razy sześcienną kostką do gry. Średnia arytmetyczna liczb oczek w
pierwszych 40 rzutach była równa 3,75, a średnia arytmetyczna liczb oczek w kolejnych
60 rzutach była równa 4,25. Średnia arytmetyczna liczb oczek w 100 rzutach jest
A. mniejsza od 4.
B. równa 4.
C. równa 4,05.
D. większa od 4,05.
83. Odchylenie standardowe danych: 1; 4; 1; 5; 9; 2; 1; 1 jest równe (z dokładnością do
części setnych);
A. 7,25
B. 2,69
C.
D. 2,40
5,75
84. Liczba 60 jest przybliżeniem z niedomiarem liczby x. Błąd względny tego przybliżenia to
4%. Liczba x jest równa
A. 57,69
B. 57,6
C. 60,04
D. 62,5
85. Cenę towaru podwyższono o 20%. O ile procent należy obniżyć nową cenę towaru, aby
po obniżce stanowiła ona 90% ceny przed zmianami?
A. o 10%
B. o 15%
C. o 25%
D. o 30%
86. Pan Krzysztof pokonuje trasę Warszawa – Kraków w czasie t ze średnią prędkością v.
Aby skrócić czas podróży o 20%, pan Krzysztof musi średnią prędkość
A. zwiększyć o 25%.
C. zmniejszyć o 20%.
B. zwiększyć o 20%.
D. zmniejszyć o 25%.
87. W tabeli podano oceny z matematyki czterech uczniów pewnej klasy.
Uczeń
Oceny
Ada
4;4;4;5;5
Basia
3;3;3;4;4
Czarek
1;1;2;2;2
Darek
1;1;5;5;5
Oceny którego ucznia wykazują największe odchylenie standardowe?
A. Ady
B. Basi
C. Czarka
D. Darka
88. Dysk twardy komputera ma rzeczywistą pojemność 500 000 MB, zaś na jego etykiecie
napisano, że dysk ma pojemność 500 GB. Wiadomo, że 1 GB = 1024 MB, zatem błąd
względny pojemności dysku (względem pojemności zapisanej w GB) jest równy:
A. 0%;
B. 2%;
C. 2,4%;
D. 3%.
89. Smartfon kosztował 800 zł. Dwukrotnie obniżono jego cenę o 20%. Obecnie smartfon
kosztuje:
A. 512 zł;
B. 480 zł;
C. 500 zł;
D. 640 zł.
90. Średnia arytmetyczna wieku Jacka i Placka jest o 6 lat większa od wieku Jacka. Stąd
wynika, że:
A. Jacek jest o 12 lat młodszy od Placka; B. Jacek jest o 12 lat starszy od Placka;
C. Jacek jest o 6 lat młodszy od Placka; D. Jacek jest o 6 lat starszy od Placka.
91. Suma dwóch liczb naturalnych jest równa 20, a ich iloczyn 64. Zatem między średnią
arytmetyczną a średnią geometryczną tych liczb zachodzi zależność:
A.
II.
ab
 ab ;
2
B.
ab
 2 ab ;
2
C.
ab
 ab  2 ;
2
D.
ab
 2 ab .
2
Działania na potęgach i pierwiastkach
92. Liczba 27 2  9 6 jest równa:
A. 9 5
B. 316
C. 6 4
D. 36
B.  1
C. 2
D. 4
1
2
93. Liczba
4  4 1
jest równa:
4 0  0,5
A. 1
94. Wartość liczby: a  163 4 jest równa wartości liczby:
A. 2
4
3
B. 2
7
3
C. 2
5
3
D. 2
14
3
4
3
8 jest równa:
16  3 3
95. Liczba:
1
2
 
7
A. -1
B.
4
49
C.  2
1
4
D. 1
4
3  1 
96. Iloraz: 32 :   jest równy
8
A. 2 27
B. 2 3
C. 2 3
D. 2 27
0
 2 2  3 1 
97. Liczba  1  2  jest równa
 2 3 
A. 1
98. Liczba
3
B. 4
 81  16
3
4


2
B. – 4

52
B. 17  4 2
C. 7  4 5
B. -1
D. 19  6 2
D. 9  4 5
Iloczyn 9 5  38 jest równy:

Liczba 2  3 2
B. 3 9

2
Liczba
C.  14  12 2
B. 22
50  18
C. 9 1
D. 9 9
jest równa:
A.  14
103.
C. 15  14 2
jest równy:
52
A. 3 4
102.
D. 4

A. 1
101.
C. 2
 4 2  2 jest równa:
A. 19  10 2
100.Ułamek
D. 36
jest równa:
A. - 8
99. Liczba 3  2
C. 9
D. 22  12 2
jest równa
2
A. 2 2
104.
Liczba
5 3  25
B. 2
C. 4
D. 10  6
jest równa
5
5
A. 5 5
4
B. 5 5
3
C. 5 5
6
D. 5 5
105.
Niech k  2  3 2 , zaś m  1 2. Wówczas wartość wyrażenia k 2  12m jest
równa:
A. 21  12 2
B. 21 12 2
C. 10
D. 34
4
106.
107.
1
Dana jest liczba: 63   . Wtedy
3
2
A. x  7
B. x  7 2
2
D. 3 7
Kwadrat liczby x  5  2 3 jest równy:
B. 25  4 3
A. 37
108.
C. x  38  7 2
5  125
Liczba
25

C. 37  20 3
D. 147
2
3
1
2
jest równa
1
B. 5 2
A. 5 2
109.
110.
Wartość wyrażenia
B. 8 2
2
√3−1
111.

3
2
√3+1
C. 44

1

0
729  4 256  2 
1
225
1
2
88
D.
C. 2
D. 2 3
2

A.
3
jest równa
B.  2 3
A. -2

Liczba 


−
D. 5
8  32  50  98 to:
Dokładna wartość wyrażenia:
A. 15 2
C. 5 0
jest równa
B.
1
15
C. 1
D. 15
2


112. Liczba  3  3  jest równa

3 

A. 4
B. 9
C.
3 3
3
D. 4  2 3
9
113.
Liczba 3 4 jest równa
1
A. 3  4 3
B. 9  4 3
C. 27  4 3
D. 3 9  3 4
114.
Wskaż równość prawdziwą
A.  256 2   2562
 2562
C.
115.
 256 D.
3
 256  3 256
665 3
92
Liczba 27  3
jest równa
1
 
3
152
3
A. 3 725
116.
B. 256 3   2563
Liczba

3
C. 3 2015
B. 31995
16  4  2

3
D. 3 2045
jest równa
B. 4 4
A. 4 4
C. 4 8
D. 4 12
8
117.
Liczba 3 3  3 9 2 jest równa
A. 3
118.
Liczba
3
B. 3
Liczba

B. 2 2012
5 3

2
D. 35
C. 21007
D. 12014
 2 15 jest równa
A. 2  2 15
120.
C. 3 4
1 2014
jest równa
2
2
A. 2 2013
119.
32
9
C. 2  4 15
B. 8


Wartość liczby a  2 5  3
A. 11
2
D. 2
jest równa
C. 19  12 5
B. 29
D. 29  12 5
121. Wartość liczby a  3 27  9 3  243 jest równa:
A. 3
122.
Liczba
A.
10
2
B. 3
5
2 1
9
2
C. 3
7
2
D. 3
jest równa liczbie:
10  5
2 
Liczba a 
B.
10  5
C.
7 5
D.
3 4
123.
2 5
jest równa liczbie
A. 2 2
124.
5
2
B. 2 7
C. 212
D. 217
C. 2 63
D. 2112
Połowa sumy 4 28  4 28  4 28  4 28 jest równa
A. 2 30
B. 2 57
7 5
4
125.
Liczba 2 3  3 2 5 jest równa
20
4
A. 2 3
126.
Wartość wyrażenia

5
3
2
Liczba
0,23
A.

1
2
1
3
C. 2 2
D. 2 2
1
2
B.
1
2
D.  1
C. 1
jest równa
25 3
4
B. 2
 32  2 1
 2 2 jest równa
4
A. 
128.
D. 2 3
C. 2 5
Liczba 2 18  32 jest równa
A. 2
127.
B. 2
53
1
B.
C.
3
52
53
129.
16
63
B. 45 9
3
1
3
1
2
1
Odwrotnością liczby 2 2  
8
Liczba
D. 5 4

B.  2
1
1
4
C. 1
D.
C. 2 1
11
A.  2 2
133.
C. 9 4
3 7
3 7
4  3 16
jest równa
8
B. 2
3
16
3 7
B.
Wartość wyrażenia
A. 2
132.
52
9
7

jest równa
7
9
Liczba
A.
131.
3
9 5  59
Liczba
jest równa
455
A. 45 40
130.
1
D.
4
3

D. 2 2
jest liczba
11
2
C. 2

11
2
11
D. 2 2
1
3
4  2 16 jest równa
1
1
1
11
A. 2 6
B. 2 4
C. 2 3
D. 212
134.
Na tablicy zapisano następujące potęgi:  2
2
2 

2
 222 




,  2
 
, 2
22
2
2 
,  2 .
2 2
Ile różnych liczb reprezentują te zapisy?
A. 4
135.
B. 3
C. 2
Liczba a  8 23  417 jest równa liczbie:
A. 2103
136.
137.
B. 4 63
2
3
1
3
B. 36 2
C. 36 4
D. 36 4
Wyrażenie

7 3

2
jest równe
Dla liczb a  2 2 i b  2  2 wyrażenie
B. 2
1
3
B.
a
jest równe
b2



C. 2 2  1
D. 4 2  2

1
6
C. 2 26
D. 2 30
Liczbą niewymierną jest:
2  3   2  3 
Liczba
A. 2

2
3
3
D.
27
jest równa
C. 7  2 3
B. 7
D. 7  2 3
. Wtedy:
A. x < 0;
72
2
2
Niech x = 8
 2  

C. 
B. 2, 13
9
16
2
142.
D. 10  2 10
Iloraz liczb 810  414 przez liczbę 63 4  6 4 jest równy
A. 1
141.
C. 10  2 21
B. 10
A.
140.
D. 32 40
A. 36 3
A. 2 2  2
139.
C. 2 59
Liczbą wymierną jest liczba:
A. 44
138.
D. 1
B. 0 < x <
1
;
3
C.
1
2
<x< ;
3
3
D. x >
2
.
3
III.
143.
Działania na logarytmach
Liczba log 0,1  log 2 16 jest równa:
B.  5
A. 6
144.
B. log 3 144
B.
Wartość liczby: 25 log
5
2
148.
D. log 2  log 3
D. 2 5
C. 5
O liczbie x wiadomo, że log 3 x  9. Zatem
1
A. x  2
B. x 
2
Liczba log 4 8  log 4 2 jest równa
B. 2
C. x  39
C. log 4 6
D. x  9 3
D. log 4 10
Wyrażenie log 4 (2x  1) jest określone dla wszystkich liczb x spełniających warunek
A. x 
150.
C. log 2  log 3
B. 4
A. 1
149.
log 12
log 2
jest równa:
A. 2
147.
D. 9
C. 2
Liczba log 6 jest równa:
A. log 2  log 3
146.
D. 7
Liczba log 3 36  log 3 4 jest równa:
A. log 3 32
145.
C. 3
1
2
B. x 
1
2
C. x  10
D. x  0
C. – 1
D. 1
Iloczyn 2 log 1 9 jest równy:
3
151.
A. – 6
B. – 4
Liczba log 3 27  log 3 1 jest równa
A. 0
152.
B. 1
B. -1
C. 0
D. 1
Liczba log 2 100  log 2 50 jest równa
A. log 2 50
154.
D. 3
Liczba log 100  log 2 8 jest równa
A. -2
153.
C. 2
Wartość wyrażenia:
A. -1
B.1
C.2
D. log 2 5000
1
log 3 15  log 3 5 jest równa:
2
B. log 2 50
C.
1
2
D. 1
155.
Liczba: log 5 5  log 5 125 jest równa:
A. -2
B.
-1
C.
1
25
D. 4
157.
Wiadomo, że log 3 8  a oraz log 3 2  b. Wynika stąd:
a
2
A. b =3a
B. b 
C. b  a
3
3
Suma: log 8 16  1 jest równa
158.
3
C. log 8 17
2
Wartość wyrażenia: log 2 20  log 2 5 jest równa
156.
A. 3
B.
A. log 2 15
159.
B. 2
B. 2
C. 3 2  c
B. 4 log 2 7
D. c 2  3
C. 4 log 2 7
3
D. 3 log 2 7
Wskaż liczbę, która spełnia równanie 4 x  9.
A. log 9  log 4
B. log 2
Dane są liczby: a  
1
; b  log 1 64; c  log 1 27. Iloczyn: abc jest równy
27
4
3
C. 2 log 9 2
log 3
B.

1
3
C.
D. 2 log 4 3
1
3
D. 3
Liczba: 2 log 5 10  log 5 4 jest równa
A. 2
166.
D. log30 – log6
Liczba: log 2 7  log 8 7 jest równa:
A. -9
165.
C. 2log6 – log12
B. 3 c  2
4
164.
D. 0
Liczba c  log 3 2. Wtedy
A. 3 log 2 7
163.
C. 1
B. log6 + 2log2
A. c 3  2
162.
D. log 2 25
Liczba log 24 jest równa
A. 2log2 + log20
161.
7
3
D.
C. 4
3
a
2
Liczba log 4  log 5  log 2 jest równa
A. 10
160.
D. b 
B. log 5 96
C. 2 log 5 6
D. 5
Liczba 8 log 4 2  2 jest równa
A. 8
B. 6
C. 4
D. 3,5
167.
1
2
Wartość wyrażenia: log 5 0,04  log 25 5  log 25 1 jest równa
B.  2
A.  3
168.
3x  1
;
2
3x  1
;
2
B. log 2 27
1
2
2x  1
.
3
D. log 4 108
log 3 15
jest liczba
log 3 5
C. 1
D. log 5 3
Wyrażenie: 27 x 3  y 3 jest równe iloczynowi:
2
 3xy  y 2



D. 3x  y 9 x

 3xy  y 
B. 3x  y  9 x 2  3xy  y 2
2
2
Wyrażenie 5a 2  10ab  15a jest równe iloczynowi:
A. 5a 2 (1  10b  3)

Równość a  2 2
A. a  14
B. 5a(a  2b  3)

2
C. 5a (a  10b  15)
D. 5(a  2b  3)
 a 2  28 2  8 zachodzi dla
B. a  7 2
C. a  7
D. a  2 2
Dla każdej liczby rzeczywistej x, wyrażenie 4 x 2  12 x  9 jest równe
A. (4x +3)(x + 3)
176.
D. log 3 2 
Działania na wyrażeniach algebraicznych

C. 3x  y 9 x
175.
2x  1
;
3
C. log 4 27
B. log 3 5
A. 3x  y  9 x 2  3xy  y 2
174.
D. log5 100
C. log 3 2 
Rozwiązaniem równania: x log 5 9  2 x 
IV.
173.
C. log5 29
Liczba log 4 9  log 2 6 jest równa
A.
172.
B. log5 8
B. log 3 2 
A. log 2 18
171.
D. 0
Niech 3 x  3 12. Wtedy:
A. log 3 2 
170.
C.  2
Liczba o 2 większa od liczby log5 4 jest równa
A. log5 6
169.
1
4
B. (2x – 3)(2x +3)
C. (2x – 3)(2x – 3)
D. (x – 3)(4x – 3)
Dla każdych liczb rzeczywistych a, b wyrażenie a – b +ab – 1 jest równe
A. (a + 1)(b - 1)
B. (1 - b)(1 + a)
C. (a - 1)(b + 1)
D. (a + b)(1 + a)
177.
A.
178.
179.
180.
ab
Po skróceniu ułamek:
ma postać:
a b
a b
B. a 2  b 2
C.
a b
D. 1
Wyrażenie 16  3x  1 jest równe
2
B. (15 - 3x)2
A. (3 - 3x)(5 + 3x)
b
, to
Jeśli a 
cb
a 1
A. b 
ac
B. b 
D. 15 – 9x2
C. (5 - 3x)(5 + 3x)
ac
a 1
C. b 
ac
a 1
D. b 
a 1
ac
Wielomian W  x 3  2 x 2  4 x  8 po rozłożeniu na czynniki ma postać:

D. W  x  2x

 4
B. W  x  2 x 2  4
A. W   x  2   x  2 
2
C. W  x  2x  2
2
2
181. Wyrażenie 3 x  1  y  jest równe:
2
A. 3x 2  y 2  1
C. 3x 2  y 2  6 xy  6 x  1
182.
B. 9 x 2  6 x  y 2  1
D. 9 x 2  y 2  6 xy  6 x  2 y  1
Po wykonaniu działań i redukcji wyrazów podobnych w wyrażeniu
3
3
W  2 x  1   x  1 otrzymamy:
A. W  7 x 3  15 x 2  3x  2
C. W  7 x 3  15 x 2  9 x  2
183.
Wyrażenie wymierne W 
A. W 
184.
16 x 2  25
po skróceniu ma postać:
16 x 2  40 x  25
4x  5
4x  5
B. W 
C. W 
B. 3a  2b 2 
2
2
 25 x
40 x  25
D. W 
C. 3a  2b 2
1
40 x
D. 3a  2b 2
Liczba 17 3  m 3 jest podzielna przez 19 dla
A. m  8
186.
4x  5
4x  5
Wyrażenie 3a 2  12ab  12b 2 może być przekształcone do postaci:
A. 3a 2  b 2 
185.
B. W  7 x 3  9 x 2  3 x  2
D. W  7 x 3  15 x 2  9 x
B. m  2
C. m  2
D. m  8


Wartość wyrażenia a  5 jest większa od wartości wyrażenia a 2  10a o
2
A. 50
B. 10
C. 5
D. 25



Jeśli 2  m 3 1  3  3  7 , to:
187.
A. m = 2;
B. x 3  6 x 2  8 x
B. 2 x 3  1
D. 4 x 3  4 x 2  9
C. 16
D. 0
Wielomian W ( x)  x 3  2 x 2  4 x  8 po rozłożeniu na czynniki ma postać wyrażenia:
B. x 2 x  4
C. x  2x  2
D. x  2x  2
2
2
Dane są wielomiany: W ( x)  x 3  3x  1 i V ( x)  2 x 3 . Wielomian W ( x)  V ( x) jest
równy:
B. 2 x 5  6 x 4  2 x 3
193.
C. 2 x 3  1
B. 8
A. x 2 x  2
192.
D. x 3  4 x 2  6 x
Dane są wielomiany: W ( x)  x 4  1 oraz V ( x)  x 4  1. Stopień wielomianu:
W ( x)  V ( x) jest równy
A. 4
191.
C. x 3  4 x 2  10 x
Dane są wielomiany: W ( x)  3x 3  2 x 2  4 i M ( x)  x 3  2 x 2  5 . Wielomian
W ( x)  M ( x) jest równy:
A. 4 x 3  9
190.
3.
Dane są wielomiany: W ( x)  x  4 i M ( x)  x 2  2 x . Wielomian W ( x)  M ( x) jest
równy:
A. x 3  2 x 2  8 x
189.
D. m = 2 –
C. m = 1 + 3 ;
Działania na wielomianach
V.
188.
B. m = 3;
B. 2 x 6  6 x 4  2 x 3
C. 2 x 5  3 x  1
D. 2 x 5  6 x 4  2 x 3
Dane są wielomiany: W ( x)  2 x 3  5x 2  3 oraz P( x)  2 x 3  12 x.
Wielomian W(x) + P(x) jest równy:
A. 5 x 2  12 x  3
B. 4 x 3  5 x 2  12 x  3
C. 4 x 6  5 x 2  12 x  3
D. 4 x 3  12 x 2  3
194.
Wielomian W ( x)  x 6  x 3  2 jest równy iloczynowi


A. x 3  1 x 2  2
195.



B. x 3  1 x 3  2




C. x 2  2 x 4  1


D. x 4  2 x  1
Wielomian W ( x)  3x 2  2 jest równy wielomianowi
2
A. 9 x 4  12 x 2  4
B. 9 x 4  12 x 2  4
C. 9 x 4  4
D. 9 x 4  4
196.
Wielomian W(x) jest stopnia czwartego. Pierwiastkiem dwukrotnym tego wielomianu
jest liczba -1. Po rozłożeniu na czynniki wielomian ten może być postaci:
A.  2x  1 x 2  1
B.  x  1  x  4
2
C.  x  1 x 2  3
2
197.
199.
B. -2
B. W ( x)  x 3  3x 2  2 x
C. W ( x)  x 3  2 x 2  x  2
D. W ( x)  x 3  2 x 2  4 x  5
Iloczyn wielomianów 2x – 3 oraz -4x2 – 6x – 9 jest równy
B.  8 x 3  27
C. 8 x 3  27
D. 8 x 3  27
Reszta z dzielenia wielomianu W ( x)  2 x 3  4 x 2  15 x  12 przez wielomian
P( x)  x  3 jest równa:
B. 57
C. -39
D. 39
Wielomian W ( x)  2 x 3  bx 2  1jest podzielny przez dwumian x + 1.
Wynika stąd, że
A. b = -3
202.
D. -4
A. W ( x)  x 4  2 x 3  x 2  2 x
A. -57
201.
C. 4
Wśród miejsc zerowych wielomianu są liczby: 0; 1; -2. Wielomian może mieć postać:
A.  8 x 3  27
200.
D. x  1x  1x  2x  3
Liczba 2 jest pierwiastkiem wielomianu W ( x)  x 3  ax 2  6 x  4. Współczynnik a
jest równy:
A. 2
198.
2
B. b = -1
C. b = 1
D. b = 3
Funkcja W jest określona wzorem W  x   3x 4  bx  2a dla wszystkich liczb
rzeczywistych. Równość W  1  W 1  0 zachodzi, gdy
A. a 
VI.
203.
2
3
B. a 
C. a  1
D. a  1
Równania, nierówności oraz układy równań i nierówności
I stopnia z jedną lub dwiema niewiadomymi
Rozwiązaniem równania
A. 8
204.
3
2
x6
2
 jest liczba:
2x  4 3
B. 10
Rozwiązaniem równania:  2 
A. -1
C.
x 1
jest liczba:
x2
B. 1
1
2
D. -10
C. 0
D.
5
3
205.
Rozwiązaniem równania
x5 2
 jest liczba
x3 3
B. 7
A. 21
206.
Rozwiązaniem równania
A. 1
207.
17
3
C.
D. 0
4
7
D. 7
Rozwiązanie równania x(x + 3)− 49 = x(x − 4)należy do przedziału
A. (;3)
208.
3x  1 2
 jest
7x  1 5
7
B.
3
C.
B. (10;)
C. (5;1)
D. (2;)
Najmniejszą liczbą całkowitą należącą do zbioru rozwiązań nierówności
3 x 5x
 
8 6 12
jest
A. 1
209.
B. 2
4 x  2 y  10
Układ równań 
ma nieskończenie wiele rozwiązań, jeśli
6 x  ay  15
A. a = −1
210.
C. a = 2
B. x = -3, y = 6
D. a = 3
C. x = 3, y = -4
Najmniejszą liczbą całkowitą spełniającą nierówność
A. -2
212.
B. a = 0
5 x  3 y  3
Rozwiązaniem układu równań 
jest para liczb
8 x  6 y  48
A. x = -3, y = 4
211.
D. – 2
C. - 1
B. -1
C. 0
D. x = 9, y = 4
x 2x 1

 jest
2
3 4
D. 1
Wskaż rysunek, na którym przedstawiony jest zbiór rozwiązań nierówności
23  x  x.
A.
B.
C.
D.
213.
3x  5 y  0
Rozwiązaniem układu równań 
jest para liczb (x, y) takich, że
2 x  y  14
A. x < 0 i y < 0
214.
B. x < 0 i y > 0
D. x > 0 i y > 0
Liczby rzeczywiste a, b, c spełniają warunki: a + b = 3, b + c = 4 i c + a = 5. Wtedy
suma a + b + c jest równa
A. 20
215.
C. x > 0 i y < 0
B. 6
C. 4
D. 1
Pięć lat temu ojciec był 3 razy starszy od syna, a za 10 lat będą mieli w sumie 90 lat.
Który układ równań opisuje tę sytuację?
5 x  3  5 y
 x  y  10  90
 x  5  3   y  5
 x  5  3   y  5
A. 
B. 
C. 
D. 
5 x  5 y  90
x  3 y
 x  y  10  90
 x  10  y  10  90
216.
Na rysunku przedstawiono geometryczną interpretację jednego z niżej zapisanych
układów równań.
Wskaż ten układ.
y  x 1
A. 
 y  2 x  4
217.
Zbiorem rozwiązań nierówności
1
2
A. (; )
218.
y  x 1
B. 
 y  2x  4
y  x 1
D. 
 y  2x  4
2  x 2x  1

 x jest przedział
3
2
B. (;
1
)
14
C. (
1
;)
14
1
2
D. ( ;)
Dane jest równanie: 3x + 4y – 5 = 0. Z którym z poniższych równań tworzy ono
układ
sprzeczny?
A. 6x + 8y – 10 = 0
C. 9x + 12y – 10 = 0
219.
y  x 1
C. 
 y  2 x  4
Rozwiązaniem równania
A. 
4
3
B. 4x – 3y + 5 = 0
D. 5x + 4y – 3 = 0
x3 1
 jest liczba
2 x 2
B. 
3
4
C.
3
8
D.
8
3
220.
Rozwiązaniem równania
x5 1
 jest liczba
7x 3
A.  11
221.
B.
C.
2
11
D. 11
Rozwiązaniem nierówności x  4  2 jest zbiór:
A.  ;6   2;
222.
11
2
B.  ;6  2;
C.  6;2
Zbiór wszystkich liczb rzeczywistych spełniających nierówność:
D.  6;2
3 2x x

 jest
5
3
6
przedziałem
223.

18
B.   ;
25

9
;  
15
A.
Rozwiązaniem równania:
224.
Równość:
m
5 5

11
B. x 3
C. x 5
D. x 6
B. m 4
C. m 1
D. m -5
Ile liczb całkowitych x spełnia nierówność: 2  x  4 ?
7
A. 14
227.
D. x  25
C. x  2
5 5
zachodzi dla
5
A. m 5
226.
12
5
Średnia arytmetyczna zestawu danych: 2, 4, 7, 8, 9 jest taka sama jak średnia
arytmetyczna zestawu danych: 2, 4, 7, 8, 9, x.
Wynika stąd, że
A. x 0
225.

9
D.   ;
5

1
;  
30
2x  4 4
 jest liczba
3 x
3
B. x 
A. x  0
C.
Układ równań:  x  y  3
B. 15
2 x  0,5 y  4
14
3
C. 16
D. 17
opisuje w układzie współrzędnych na płaszczyźnie
A. zbiór pusty
B. dokładnie jeden punkt
C. dokładnie dwa różne punkty
D. zbiór nieskończony
228.
Para liczb x = 2 i y = 1 jest rozwiązaniem równań  x  ay  5 , gdy
2 x  y  3
A. a  3
B. a  2
C. a  2
D. a  3
229.
Wskaż nierówność, która opisuje zaznaczony na osi liczbowej przedział otwarty
 4;2.
A. x  1  3
230.
B. x  3  1
C. x  1  3
Na jednym z poniższych rysunków przedstawiono interpretację geometryczną układu
równań:
 x  3 y  5

3x  2 y  4
Wskaż ten rysunek.
A.
B.
C.
231.
D. x  3  1
D.
Najmniejszą liczbą całkowitą spełniającą nierówność 2x  2  4x  1  1 jest
A.  2
B.  1
C. 0
D. 1
232.
Na rysunku przedstawiono wykresy trzech parami przecinających się prostych.
Te proste to
x  2 y  1
x  2 y  1
A. 3 x  y  11
3 x  8 y  17
B. 3 x  y  11
3 x  8 y  17
x  2 y  1
x  2y 1
D. 3x  y  11
3x  8 y  17
C. 3 x  y  11
3 x  8 y  17
233. Równanie
3 2  x 3
 nie ma takiego samego rozwiązania, jak równanie
4x  3
2
A. 6  2  x   3  4 x  3
2
 6  3x   4 x  3 C. 9  2  x   2  4x  3
3
3
D. 3  2  x    4 x  3
2
B.
234. Zbiór rozwiązań nierówności x  3x  2 to

A.  ;1  3
235.


B.  ;1  3


C.  1  3;


D.  1  3;

Liczba 4 spełnia nierówność a 2 x  16  0 z niewiadomą x wtedy i tylko wtedy, gdy
A. a   2;2
B. a   ;2  2;
C. a   2;2
D. a   ;2
236. Rozwiązaniem nierówności  1  2x  3  3 jest zbiór
A.  ;1  3;
B. 1; 3
C.  1;3
D.  2; 3.
x  y
 2  x  2
237. Rozwiązaniem układu równań 
jest para liczb:
x

y

 2  y  1
A. dodatnich
VII.
238.
Zbiorem rozwiązań nierówności:  x  1x  3  0 jest:
B. (;3    1;)
B. ma dwa pierwiastki
C. ma jeden pierwiastek
D. nie ma pierwiastków
B. (2;1)
C. (;1)  (2;)
D.  1;2
Większa z liczb spełniających równanie: x 2  6 x  8  0 to:
A. 2
242.
D.  1;3
Zbiorem rozwiązań nierówności: x  1x  2  0 jest zbiór:
A.  ;2  1;
241.
C. (;1    3;)
Równanie x 2  6 x  9  1
A. ma trzy pierwiastki
240.
D. nie ma rozwiązania
Równania i nierówności II stopnia z jedną niewiadomą
A.  1;3
239.
C. różnych znaków
B. ujemnych
B. 4
C. -2
D. -4
Do zbioru rozwiązań nierówności: 9  x 2 należy liczba
A. -2
B. 0
C. -3
D. 2
243.
Zbiór rozwiązań nierówności (x +1)(x −3) >0 przedstawiony jest na rysunku
244.
Do zbioru rozwiązań nierówności (x − 2)(x + 3) <0 należy liczba:
A. 9
245.
B. 7
C. 4
D. 1
Wskaż, który zbiór przedstawiony na osi liczbowej jest zbiorem liczb spełniających
jednocześnie następujące nierówności: 3(x −1)( x −5) ≤ 0 i x >1.
246.
Liczby x1 ; x2 są różnymi rozwiązaniami równania 2 x 2  3x  7  0 . Suma x1  x2 jest
równa:
7
7
3
3
A. 
B. 
C. 
D. 
2
4
2
4
247.
Zbiorem rozwiązań nierówności x(x + 6) < 0 jest:
B. 0;6
A.  6;0
248.
C.  ;6  0;
Liczby x1 ; x2 są pierwiastkami równania x 2  10 x  24  0  x1  x2 . Oblicz: 2x1  x2 .
A. -22
249.
B. -17
x  3x  5  0
1
1

 1
x1 x 2
B.
1
1
1


x1 x 2 4
1
1
1


x1 x 2 2
D.
C. 0,5 oraz 2
D. -2 oraz 2
B. -3
C. -2
D. -1
Zbiorem rozwiązań nierówności x 2  5 jest

 
5 ;


B.  ;  5 
5; 
C.
5;   
D. 5;  
Rozwiązaniem nierówności: m  52  0 jest zbiór:
B. 
A. R
C. {5}
D. {-5}
Rozwiązaniem nierówności  x  52  0 jest:
A. zbiór liczb rzeczywistych
256.
C.
Mniejszą z dwóch liczb spełniających równanie x 2  5 x  6  0 jest
A.  ; 5 
255.
1
1

0
x1 x 2
B. 0 oraz 0,5
A. -6
254.
1
2

x3 x5
Równanie: (2x – 1)(x – 2) = (1 – 2x)(x + 2) ma dwa rozwiązania. Są to liczby
A. -2 oraz 0,5
253.
x 2  2 x  15
0
x2  3
x 2  2 x  15
0
D.
x 2  25
Pierwiastki x1; x2 równania: 2(𝑥 + 2)(𝑥 − 2) = 0 spełniają warunek:
A.
252.
D. 13
B.
x2  9
C.
251.
C. 8
Wskaż równanie, którego rozwiązaniami są liczby: -3 oraz 5.
A.
250.
D.  ;0  6;
B. zbiór pusty
C. liczba -5
D. liczba 5
Różnica między większym i mniejszym rozwiązaniem równania ( x + 7)( x + 1) = 0
jest równa:
A. -8
B. -6
C. 6
D. 8
257.
Równanie x  1  x  1
x 1
A. ma dokładnie jedno rozwiązanie: x = 1; B. ma dokładnie jedno rozwiązanie: x = 0;
C. ma dokładnie jedno rozwiązanie: x = -1; D. ma dokładnie dwa rozwiązania: x = 0, x = 1
258. Równanie 2 x 2  11x  3  0
A. nie ma rozwiązań rzeczywistych; B. ma dokładnie jedno rozwiązanie rzeczywiste;
C. ma dwa dodatnie rozwiązania rzeczywiste; D. ma dwa ujemne rozwiązania rzeczywiste.
259.
Wśród podanych poniżej nierówności wskaż tę, której zbiorem rozwiązań jest
przedział  3,1 .
A. xx  2  3
260.
B. xx  4  1
C. xx  3  1
D. xx  1  3
Równanie  x 2  6 x  2  k ma trzy rozwiązania. Wynika stąd, że k jest równe:
A. 3
B. 2 11
C. 11
D.
11
2