Podstawy Elektrotechniki - Stany nieustalone
II. Metoda Operatorowa
Zadanie o.1
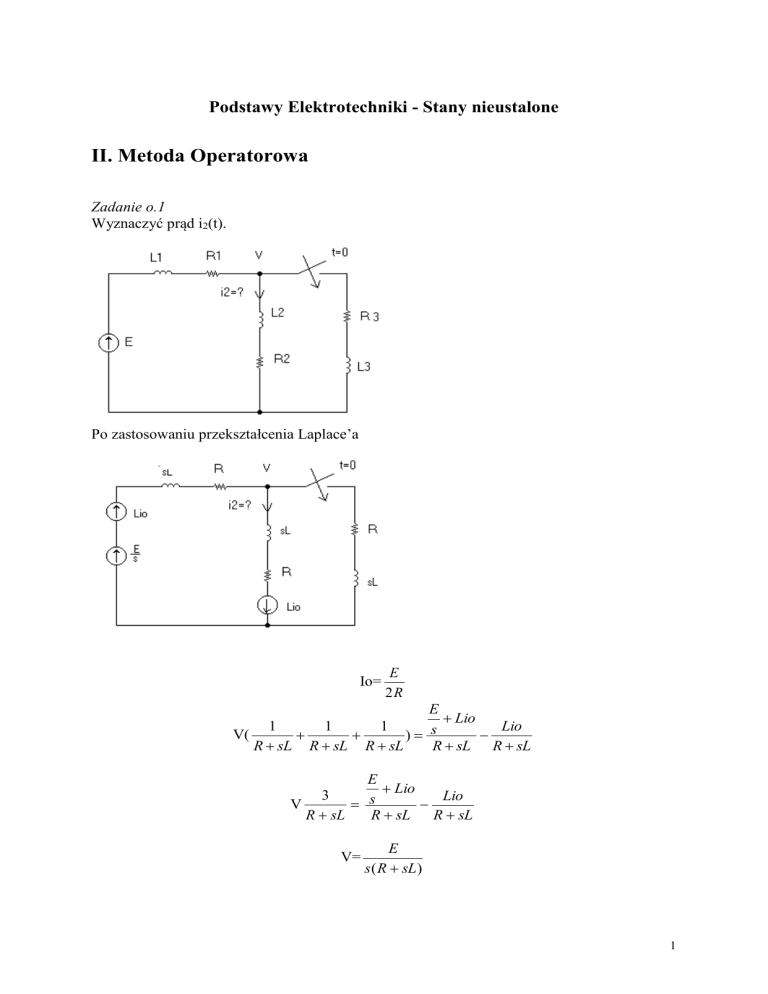
Wyznaczyć prąd i2(t).
Po zastosowaniu przekształcenia Laplace’a
Io=
E
2R
E
Lio
1
1
1
Lio
V(
) s
R sL R sL R sL
R sL R sL
E
Lio
3
Lio
s
V
R sL
R sL R sL
V=
E
s( R sL )
1
V
E
E
R sL 3s ( R sL ) 3Ls ( R s )
L
R
R
E
E Lt
E
E Lt
i 2 (t )
e
[
e ]
3R 3R
3R 3R
I 2 (s)=
Zadanie o.2
Obliczyć napięcie na zaciskach wyłącznika w chwili t=0 i napięcia na C1 i C2 w chwili t=T.
a) t=0:
E
s
E
EC3
EC3
E
1
s
J (s)
1
2 RC 3 s 1 2 RC 3 s 1
1
1
2R
2R
(s
)2 RC 3
(s
)
C3 s
2 RC 3
2 RC 3
C3 s
1
E 2 RC3 t
i (t ) L {J ( s)}
e
2R
1
t
1
1
U c 3 (t )
i (t )dt
C3 0
C3
1
t
1
t
E 2 RC3 t
1 E
2 RC3 t
e
dt
[
2
RC
e
]0
3
0 2R
C3 2R
1
1
E
[2 RC 3 e 2 RC3t 2 RC 3 ] E (1 e 2 RC3
C3 2R
1
1
t
E
E t
U R (t ) i (t ) R
Re 2 RC3 e 2 RC3
2R
2
U wyl (t ) U c3 (t ) U R (t ) E (1 e
1
2 RC3
1
1
1
t
E t
1 t
) e 2 RC3 E (1 e 2 RC3 e 2 RC3 )
2
2
b) t=T
J ( s)
E
s
1
R
s(C1 C2 )
E (C1 C2 )
Rs (C1 C2 ) 1
E (C1 C2 )
E
1
1
1
R
(s
s
RC (C1 C2 ) R(C1 C2 )
RC (C1 C2 )
1
t
E
J (t ) L {J ( s)} e R (C1 C2 )
R
Obliczamy napięcie na C1 i C2 pamiętając że: Cz=C1+C2
1
2
t
1
1
U c1 (t ) U c 2 (t )
i (t )dt
Cz 0
Cz
t
1
1
t
E R (C1 C2 ) t
E
RC ( C1 C2 ) t
e
dt
[
RC
(
C
C
)
e
]0
1
2
0 R
RC z
1
1
t
ER(C1 C 2 ) R (C1 C2 ) t ER(C1 C2 )
e
E (1 e R (C1 C2 ) )
R(C1 C2 )
R(C1 C2 )
Zadanie o.3
Wyznaczyć rozpływ prądów w układzie przedstawionym poniżej dla dwóch przypadków
zamykania i otwierania wyłącznika.
Dla obwodu przedstawionego na rysunku równania różniczkowe mają postać:
di
di
R1i1 L1 1 M 2 u1
dt
dt
di
di
M 1 R2 i2 L2 2 u 0
dt
dt
Te same równania w rachunku operatorowym:
(R1+sL1)I1(s)-sMI2(s)=U1(s)+L1i1(0)-Mi2(0)
-sMI1(s)+(R2+sL2)I2(s)=L2i2(0)-Mi1(0)
Przy zerowych warunkach początkowych równania powyższe upraszczają się do postaci
Z1(s)I1(s)-sMI2(s)=U1(s)
-sMI1(s)+Z2(s)I2(s)=0
przy czym:
Z1(s) – impedancja operatorowa obwodu 1;
Z2(s) – impedancja operatorowa obwodu 2.
1. Zamykanie wyłącznika.
U
Z równań przy U ( s )
otrzymujemy
S
Z 2 (s)
U
2
2
Z1 ( s ) Z 2 ( s ) s M s
M
I 2 ( s)
U
Z1 ( s ) Z 2 ( s ) s 2 M 2
I1 ( s )
3
Po podstawieniu: Z1(s)=R1+sL1; Z2(s)=R2+sL2; L1L2=M2 otrzymujemy
I1 ( s )
sL2 R2
U
s[ s ( L1 R2 L2 R1 ) R1 R2 ]
R2
UL2
L2
I1 ( s )
R
L1 R2 L2 R1
1 R2
s[ s
]
L1 R2 L2 R1
s
Rozkładamy na ułamki proste
I1 ( s )
UL2
L R L2 R1 1 L1 R2
[ 1 2
L1 R2 L2 R1
L2 R1
s L2 R1
I1 ( s )
Po podstawieniu
L1 R2
U 1
[
R1 s L1 R2 L2 R1
1
]
R1 R2
s
L1 R2 L2 R1
1
R1 R2
s
L1 R2 L2 R1
L1
L
1 , 2 2 otrzymujemy przebieg prądu
R1
R2
t
1
U
i (t ) [1
e 1 2 ]
R1
1 2
Prąd w obwodzie 2
I 2 ( s)
I 2 ( s)
MU
s ( L1 R2 L2 R1 ) R1 R2
MU
L1 R2 L2 R1
1
R1 R2
s
L1 R2 L2 R1
t
MU
i2 (t )
e 1 2
L1 R2 L2 R1
Prądy w stanie ustalonym:
i1u
U
; i2 u 0
R1
2. Otwieranie wyłącznika.
4
Po otwarciu wyłącznika obwód 1 zostaje przerwany, więc i1=0. Prąd może płynąć tylko w
obwodzie
2.
I1 ( s ) 0; i1 (0)
W
celu
jego
obliczenia
podstawimy
w
równaniach:
U
; i2 (0) 0 przyjmując, że przy zamkniętym wyłączniku został uprzednio
R1
osiągnięty stan ustalony.
I 2 ( s )( sL2 R2 ) Mi1 (0)
I 2 (s)
MU
L2 R1
MU
R1
1
R
s 2
L2
stąd
t
MU 2
i2 (t )
e
L2 R1
Zadanie o.4
W obwodzie jak na rysunku w chwili t=0 zamknięto wyłącznik W. Obliczyć przebiegi napięć
na obydwu kondensatorach, jeżeli wiemy, że u1(0) = u2(0) = 0.
T=0
R
R
W
C
C
E
=
const
U
1(t)
U
2(t)
Rozwiązanie:
Korzystając z metody potencjałów węzłowych otrzymujemy:
5
U 1 ( p)
E
pR
1
pC
R
1
R
E ( RCp 1)
p[( RC ) 2 p 2 3RCp 1]
1
pC
U 1 ( p)
1
E
2
2
1 pC p[( RC ) p 3RCp 1]
R
pC
Przy przejściu na postać czasową korzystamy z I wzoru Heaviside’a.
U 2 ( p)
Równanie ma postać: H(p)=(RC)2p2+3RCp+1=0 posiada dwa następujące pierwiastki:
3
3 2
1 2
1
p1, 2
(
) (
)
(1,5 1,118)
2 RC
2 RC
RC
RC
0,382
2,618
p1
p2
RC
RC
Po obliczeniach mamy:
RCp1 1
RCp 2 1
p1t
u1 (t ) E [1
e
e p2t ]
2
2
( RC ) p1 ( p1 p 2 )
( RC ) p 2 ( p 2 p1 )
E [1 0,723e
0 , 328t
RC
0,276e
2 , 618t
RC
] 1(t )
e p1t
e p2t
u 2 (t ) E [1
]
( RC ) 2 p1 ( p1 p 2 ) ( RC ) 2 p 2 ( p 2 p1 )
E [1 1,170 e
0 , 382t
RC
0,170 e
2 , 618t
RC
] 1(t )
Zadanie o.5
Wyznaczyć napięcia na kondensatorze.
6
1
E E
E
I 2 ( R )
I 1 ( s ) R
sC1
s 2s 2s
1
I1 ( R) 0
I 2 ( s ) R R
sC 2
I 1 ( s )RsC 1 1 I 2 ( s ) RsC 1 E
I 1 ( s ) RsC 2
C1
2
I 2 (s)
(2 RsC 2 1) 0
2
Wg
RsC 1 1 RsC 1
R 2 C1C 2 s 2 s ( RC 1 2 RC 2 ) 1
RsC 2 2 RsC 2 1
W I1
E
WI 2
C1
2
0
RsC 1
2 RsC 2 1
RsC 1 1 E
RsC 2
E
C1
(2 RsC 2 1)
2
C1
C1
RsC 2
2 E
2
0
E
C1C 2 Rs
2
I 2 ( s) 2
R C1C 2 s 2 ( RC 1 2 RC 2 ) s 1
E
C1 R
2
U C 2 (s) 2
R C1C 2 s 2 ( RC 1 2 RC 2 ) s 1
C1 C 2 C
M ( s ) s 2 C 2 R 2 s3RC 1
9( RC ) 2 4C 2 R 2 5( RC ) 2
r1, 2
3
5
2 RC 2 RC
0.76 0.38
2 RC
RC
3 2.24 2.62
s2
2 RC
RC
s1
7
E
E
1
1
r
t
r
t
2
U C 2 (s)
e1
e2
2.62 0.38
RC ( s s1 )( s s 2 ) 2 RC 0.38 2.62
RC
RC
RC
RC
E 1 r1t
1
U C 2 (t )
e
e r2t
2.24
2 RC 2.24
RC
RC
E 1
E
U C 2 (t )
e r1t e r2t
e r1t e r2t
2 2.24
4.48
Zadanie o.6
Wyznaczyć uc(t) dla wymuszenia przedstawionego na rys. o.6
Rys. o.6 Przebieg e(t) i jego rozkład na składowe e1, e2.
Przebieg e(t) można przedstawić jako sumę przebiegów e1(t) i e2(t).
8
e1 t
E
1
t
e2 t
E
et
E
1
1
t
t 1
E
1
t 1
Przechodząc na postać operatorową:
E s
E
E s 1
E
e
1 e s 1
2
2
2
1s 1s
1s
Napięcie na kondensatorze wyznaczamy następująco:
Es I s R U s Es U s I s R
1
E s U s 1
1
1
*
E s *
U s *
sC
R
sC
sRC
sRC
1
1
U s * 1
E s *
sRC
sRC
U s * sRC 1 E s
U s I s *
U s
E s
1 sRC
E s
1
RC s
RC
E
1 e s1
1s 2
E 1 e s1
E
U s
1
1 1 RC
2
RC s
1 s RC s
RC
RC
1
1
e s1
1
1
2
2
s s RC s s RC
Opierając się na zależności :
a2
at 1 e at
s 2 s a
Otrzymujemy:
9
2
1
E
RC
U s
2
1
1 RC
RC
1
1
e s 1
1
1
2
2
s s RC s s RC
2
1 2
1
E RC
RC
s 1
e
1 2
1
1
2
1
s
s
s
s
RC
RC
RC
Przechodząc na postać czasową otrzymujemy :
U t
1
1
1
t
t
ERC 1
t 1 1 e RC 1
t 1 e RC
1 RC
RC
Zadanie o.7
e(t)=E+E(t-τ)-2E(t-2τ)
E(s)=
E E s 2 E 2s
e
e
s s
s
10
E(s)=I(s)R+I(s)SL
E(s)=I(s)(R+SL)
I(s)=
1
1
E
S
[ S
e s
R
R
L
( S) ( S)
L
L
E (s)
I (s)
R
L( S )
L
2
E
1
e s
2e 2s
S
e 2s ] [
]
R
R
R
R
L
( S)
S (S ) S (S ) S (S )
L
L
L
L
Korzystając z zasady:
f(t)=
F1 ( s )
F2 ( s)
=Σ
F1 ( s k )
'
2
F (s k )
e st
otrzymujemy:
R
R
1
1 Lt
1
1 RL (t ) 1
E
1 L (t 2 )
e )(
i(t)= [(
e
)
e
) ]
R
R
R
R
R
R
L
L
L
L
L
L
L
R
i(t)=
R
R
R
R
R
t
( t )
( t 2 )
t
( t )
( t 2 )
E
E
[(1 e L ) (1 e L
) (1 e L
] [1 e L e L
e L
]
R
R
Zadanie o.8
W obwodzie przedstawionym na rysunku obliczyć napięcie na cewce.
11
Napięcie zasilające ma postać:
Poszczególne przebiegi wynoszą;
E
e (t) t 1(t)
1
T
E
e (t) t 1(t T)
2
T
E
e (t) t 1(t 2T)
3
T
E
e (t) t 1(t 3T)
4
T
e (t) 2E 1(t 4T)
5
Całkowity przebieg napięcia
e(t) e (t) e (t) e (t) e (t) e (t)
1
2
3
4
5
E
E
E
E
e(t) t 1(t) t 1(t T) t 1(t 2T) t 1(t 3T) 2E 1(t 4T)
T
T
T
T
czyli
E(s)
I(s)
E 1 E 1 sT E 1 s2T E 1 s3T
1
e
e
e
2E e s4T
T s2 T s2
T s2
T s2
s
E(s)
(3R sL)
Tym samym napięcie UL:
E(s)
U (s)
sL
L
(3R sL)
Po podstawieniu do wzoru na napięcie
12
E 1 E 1 sT E 1 s2T E 1 s3T
1
e
e
e
2E e s4T
T s2 T s2
T s2
T s2
s
U (s)
sL
L
3R sL
EL
ELe sT
ELe s2T
ELe s3T
2ELe s4T
U (s)
L
Ts(3R sL) Ts(3R sL) Ts(3R sL) Ts(3R sL)
(3R sL)
Obliczamy poszczególne człony
EL
EL
U1 (s)
L
Ts(3R sL) TL
1
3R
s(s
)
L
3R
3R
t
t
E L
E
u1 (t)
(1 e L )
(1 e L )
L
TL 3R
T3R
ELe sT
EL e sT
U 2 (s)
L
3R
Ts(3R sL) TL
s(s
)
L
3R
3R
(t T)
(t T)
E
L
E
u 2 (t)
1(t T) e L
1(t T)
1(t T) e L
1(t T)
L
TL 3R
T3R
ELe s2T
EL e s2T
U 3 (s)
L
3R
Ts(3R sL) TL
s(s
)
L
3R
(t 2T)
E
L
L
u 3 (t)
1(t 2T)
1(t 2T) e
L
TL 3R
ELe s3T
EL e s3T
U 4 (s)
L
3R
Ts(3R sL) TL
s(s
)
L
3R
(t 3T)
E
L
L
u 4 (t)
1(t 3T)
1(t 3T) e
L
TL 3R
3R
(t 2T)
E
L
1(t 2T)
1(t 2T) e
T3R
E
T3R
3R
(t 3T)
L
1(t 3T)
1(t 3T) e
13
2ELe s4T
e s4T
U 5 (s)
2E
L
3R
(3R sL)
(s
)
L
3R
(t 4T)
u 5 (t) 2E e L
1(t 4T)
L
Napięcie na cewce wynosi
u (t) u1 (t) u 2 (t) u 3 (t) u 4 (t) u 5 (t)
L
L
L
L
L
L
E
u (t )
T3R
3R
3R
t
(t T)
1(t T)
(1 e L ) - 1(t T) e L
3R
3R
(t 2T)
(t 3T)
1(t 2T) e L
1(t 2T) 1(t 3T) e L
1(t 3T)
3R
L (t 4T)
- 2Ee
1(t 4T)
Zadanie o.9
Obliczyć przebieg prądu w obwodzie jeżeli w układzie działa wymuszenie o przebiegu jak na
rysunku:
Rozkładamy podaną funkcję na składowe:
T
3
e(t ) E1(t ) E1(t ) E1(t T ) E1(t T ) E1(t 2T ) ...
2
2
dokonujemy przekształcenia Laplace’a
14
T
3
E ( s ) L[ E1(t ) E1(t ) E1(t T ) E1(t T ) E1(t 2T ) ...]
2
2
T
3
E E s
E
E sT E
E ( s ) e 2 e sT e 2 e 2T ...
s s
s
s
s
sT
3
sT
E
E ( s ) (1 e 2 e sT e 2 e 2 sT ...)
s
Wyrażenie w nawiasie jest ciągiem geometrycznym więc:
E
1
E ( s) (
)
sT
s
1 e 2
Obliczamy prąd w obwodzie:
T
3
s
sT
E
sT
3
sT
Cs(1 e 2 e sT e 2 ...)
E ( s)
E ( s ) * Cs s
E 1 e 2 e sT e 2 ...
J (s)
*
1
1
1
RsC 1
s
R
(s
) RC
(s
)
sC
RC
RC
Dokonujemy odwrotnego przekształcenia Laplace’a
1
i (t ) L1{J ( s)}
1
T
1
t
(t )
( t T )
E
T
* [e RC *1(t ) e RC 2 *1(t ) e RC
*1(t T )...]
R
2
Zadanie o.10
Określić odpowiedź u(t) układu RL na napięcie wymuszające e(t) jak na rysunku
R
e(t)
L
UL
e(t)
2E
E
T
t
15
Zadanie o.11
Wyznaczyć napięcie na kondensatorze dla wymuszenia przedstawionego poniżej.
16
T
e(t ) E m sin t 1(t ) 2 E m sin t 1 t E m sin t 1t T
2
E (s) 1
U C ( s)
1 sC
R
sC
E (s)
U C ( s)
1 sRC
T
T T
e(t ) E m sin t 1(t ) 2 E m sin t 1 t E m sin t T T 1(t T )
2
2
2
j
1
E ( s) E m
2Em e
s j
2
gdzie :
T
U C ( s)
T
2
e
T
s
2
1
1
E m e jT e Ts
s j
s j
T
s
E
E (s)
1
1
m 1 2e j e 2 e 2 Ts
1 sC RC
( s j ) s 1
R
sC
RC
1
T
1
t
t
j T2 jt
Em
1
T
j t
RC
2 RC
RC
U C (t )
2
e
e
1
(
t
)
2
e
e
e
e
1 t
RC 1
2
j
RC
T
1
t
j T j t
RC
RC
e e e e
1(t T )
Zadanie o.12
Wyznaczyć UL(t) dla napięcia zasilania e(t) jak na wykresie.
17
Napięcie wymuszające:
e(t ) E m sin t1(t ) E m sin t1(t
T
)
2
T
E ( s) E m
s
1
1
Em e 2
s j
s j
Odpowiedź układu:
T
s
E ( s)
U L ( s)
sL E m 1 e 2
R sL
s
s
( s j )( s R )
L
A
B
sa sb
R
)
L
A( s b) B( s a)
s
( s a)( s b)
( s a)( s b)
As Bs Ab Ba s
( s j )( s
A B 1
Ab Ba 0
A 1 B
b(1 B) Ba 0
b B(b a ) 0
b
B
ba
a
A
ba
T
at
bt
1
(
t
)
1
(
t
)
(
Ae
Be
)
R
2
( j )
L
Po podstawieniach otrzymamy:
L
L
R
j (t ar ctg )
jar ctg
t
Em
R
R
U L (t )
Re
e L 1(t )
Le
2
2
( R (L)
U L (t ) E m
1
L
L
RT
R
j (t ar ctg )
ar ctg
t
T
R
R
2L
Le
Re
e e L 1(t )
2
R 2 (L) 2
Em
Przyjmijmy oznaczenie:
ar ctg
L
R
u L (t ) ( E m sin cos(t ) E m cos sin e
RT
( E m sin cos(t ) E m cos sin e 2 L e
R
t
L
R
t
L
)1(t )
T
)1(t )
2
Ostatecznie:
18
0
R
t
1
u L (t ) E m sin cos(t ) E m sin 2e L
2
RT
R
t
1
2L
L
E
sin
2
(
1
e
)
e
m
2
dla t 0
dla 0 t
dla t
T
2
T
2
Zadanie o.13
Wyznaczyć i(t) dla napięcia zasilania e(t) jak na wykresie.
Funkcję napięcia e(t) można rozłożyć na trzy składowe:
19
e( t )
e( s)
E
t
2E
(t )
E
(t 2 )
E 1 2 E 1 s E 1 2 s E 1
e
e
1 2e s e 2 s
s2 s2
s2
s2
Prąd w obwodzie obliczamy z :
I ( s)
Szukamy obrazu funkcji
e ( s)
e ( s)
E (1 2e s e 2 s )
R
R sL L( s R )
s 2L( s )
L
L
1
s (s a)
2
gdzie a=
R
L
1
As B
C
( As B)( s a ) C ( s) 2 As 2 Bs Aas Ba Cs2
s2 (s a)
s2
sa
s2 (s a)
s2 (s a)
Porównujemy współczynniki:
A+C=0
B+Aa=0
aB=1 B=
1
a
A=
1
a2
C=
1
a2
Podstawiamy A B C
1
1
1
2
2
1
1 1 1 1 1
a 2s a2 a 2 * * 2 2 *
s
s
sa a s a s a sa
Przechodząc na postać czasową:
1
1
1
1(t ) t 2 e at
2
a
a
a
Podstawiając
R
R
t
( t )
1
1
1
1
1
1
L
L
* 1(t )
R 1(t ) R t R e * 1(t ) 2 R 1(t ) R 1(t ) R e
( )2
( ) 2
( )2
( )2
E
L
L
L
L
L
L
I (t )
L
R
( t 2 )
1 1(t 2 ) 1 1(t 2 ) 1 e L
* 1(t 2 )
R
R 2
R 2
(
)
(
)
L
L
L
20
