Wzory z matrematyki

Wzory z matematyki
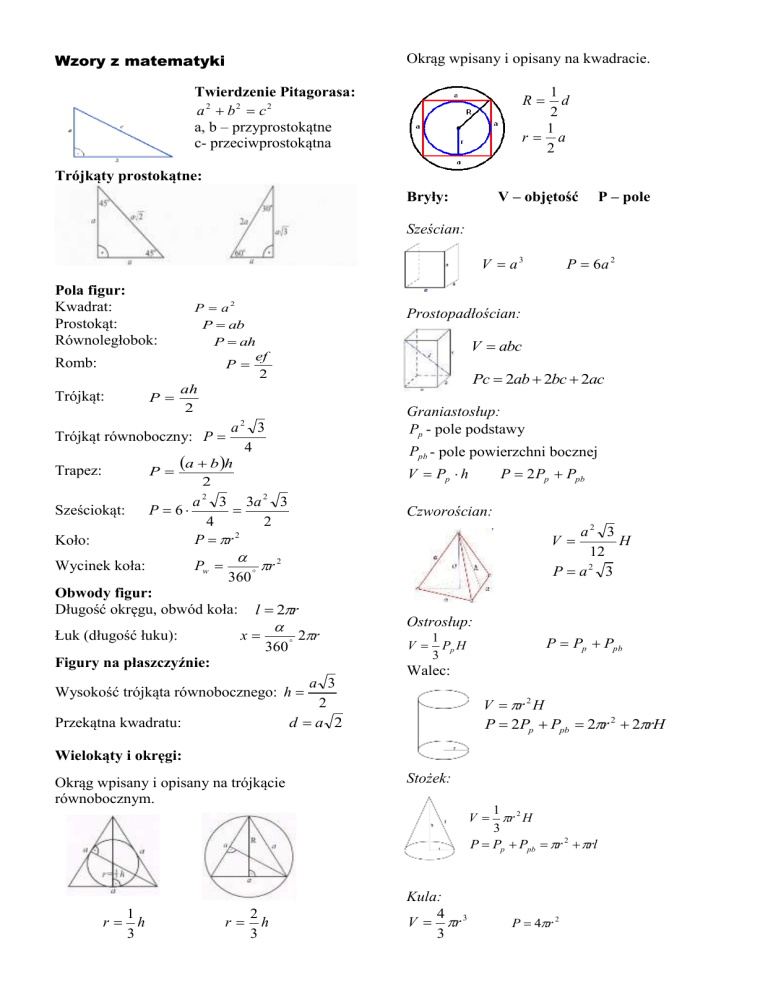
Okrąg wpisany i opisany na kwadracie.
1
d
2
1
r a
2
Twierdzenie Pitagorasa:
a 2  b2  c 2
a, b – przyprostokątne
c- przeciwprostokątna
R
Trójkąty prostokątne:
Bryły:
V – objętość
P – pole
Sześcian:
V  a3
Pola figur:
Kwadrat:
Prostokąt:
Równoległobok:
P  a2
P  ab
P  ah
Prostopadłościan:
V  abc
ef
P
2
Romb:
Trójkąt:
ah
P
2
a2 3
Trójkąt równoboczny: P 
4
a  b h
P
Trapez:
Koło:
a 2 3 3a 2 3
P  6

4
2
2
P  r
Wycinek koła:
Pw 
Pc  2ab  2bc  2ac
Graniastosłup:
Pp - pole podstawy
Ppb - pole powierzchni bocznej
V  Pp  h
2
Sześciokąt:


P  6a 2
P  2 Pp  Ppb
Czworościan:
a2 3
H
12
P  a2 3
V 
r 2
360
Obwody figur:
Długość okręgu, obwód koła: l  2r

x
2r
Łuk (długość łuku):
360 
Figury na płaszczyźnie:
a 3
Wysokość trójkąta równobocznego: h 
2
Przekątna kwadratu:
d a 2
Ostrosłup:
V
1
Pp H
3
P  Pp  Ppb
Walec:
V  r 2 H
P  2Pp  Ppb  2r 2  2rH
Wielokąty i okręgi:
Okrąg wpisany i opisany na trójkącie
równobocznym.
1
r h
3
r
2
h
3
Stożek:
1
V  r 2 H
3
P  Pp  Ppb  r 2  rl
Kula:
4
V  r 3
3
P  4r 2
Procenty (symbol - %):
Promile (symbol - ‰)
1% 
1‰ 
1
 0,01
100
Suma kątów wewnętrznych trójkąta jest równa
1800.
1
 0,001
1000
α + β + γ = 180O
Potęgi:
a 1
0
a
n
1
 n
a
1
n
a n a
Iloczyn potęg o tych samych podstawach
a m  a n  a mn
Trójkąt równoboczny:
Wszystkie boki są równe.
Wszystkie kąty są równe.
Iloraz potęg o tych samych podstawach
am
a m : a n  n  a m n
a
(a m ) n  a mn
Potęga potęgi:
Iloczyn potęg o tym samym wykładniku:
a n  b n  (ab) n
W trójkącie suma długości dwóch dowolnych
boków jest większa od długości trzeciego boku.
a+b>c
a+c>b
b+c>a
Iloraz potęg o tym samym wykładniku:
an  a 
a :b  n  
b
b
n
n
n
Pierwiastki:
a  b....bo....b 2  a
np.
4  2 bo 22 = 4
ab  n a  n b
np.
12  4  3  4  3  2 3
2  18  2  18  36  6
Twierdzenie Talesa:
Jeżeli ramiona kąta przetniemy kilkoma
prostymi równoległymi, to odcinki wyznaczone
przez te proste na jednym ramieniu kąta są
proporcjonalne do odpowiednich odcinków na
drugim ramieniu kąta.
a c

b d
n
Kąty:
Kąt środkowy jest dwa razy większy od kąta
wpisanego opartego na tym
samym łuku.
S – środek okręgu
α – kąt środkowy
β – kąt wpisany
α = 2β
Kąty wierzchołkowe są równe.
a b

c d
W figurach podobnych stosunki odpowiednich
boków są równe.
F’ ~ F – czytamy: figura F’ jest podobna do
figury F
a ' b' c ' d '
  
a b c d