PODOBIEŃSTWO FIGUR. TWIERDZENIE TALESA KLASA II

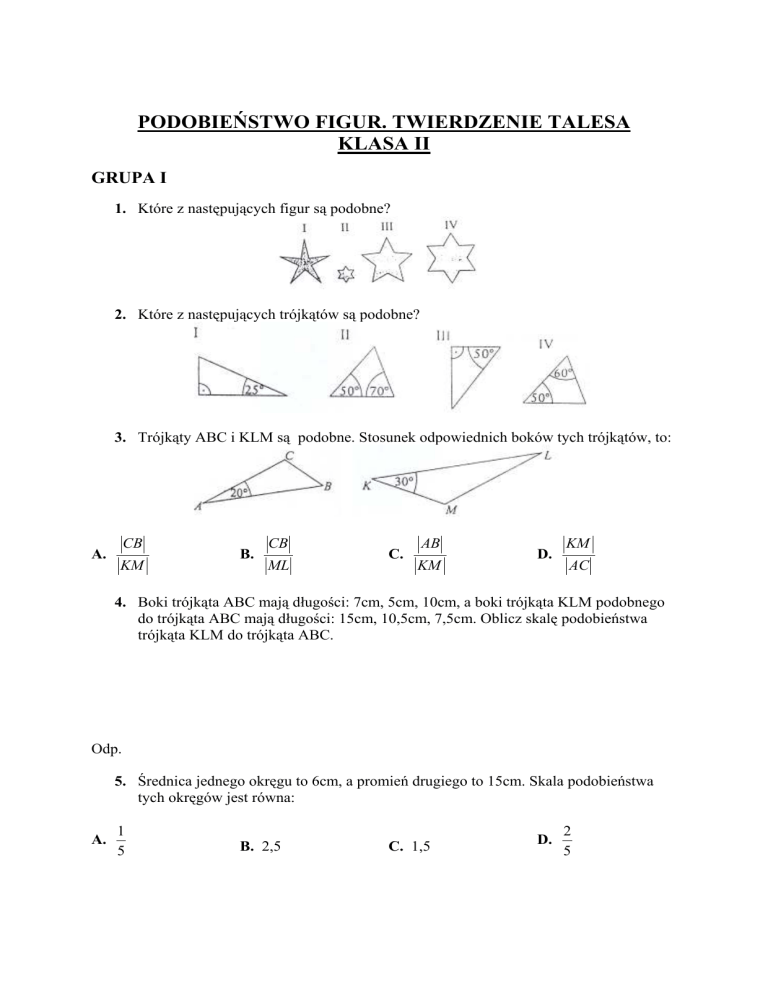
PODOBIEŃSTWO FIGUR. TWIERDZENIE TALESA
KLASA II
GRUPA I
1. Które z następujących figur są podobne?
2. Które z następujących trójkątów są podobne?
3. Trójkąty ABC i KLM są podobne. Stosunek odpowiednich boków tych trójkątów, to:
CB
A.
CB
B.
KM
AB
C.
ML
KM
D.
KM
AC
4. Boki trójkąta ABC mają długości: 7cm, 5cm, 10cm, a boki trójkąta KLM podobnego
do trójkąta ABC mają długości: 15cm, 10,5cm, 7,5cm. Oblicz skalę podobieństwa
trójkąta KLM do trójkąta ABC.
Odp.
5. Średnica jednego okręgu to 6cm, a promień drugiego to 15cm. Skala podobieństwa
tych okręgów jest równa:
A.
1
5
B. 2,5
C. 1,5
D.
2
5
6.
A.
B.
C.
D.
Dwa romby są zawsze podobne, jeśli:
sumy miar dwóch kątów wewnętrznych tych rombów są równe
kąt ostry jednego rombu jest równy 45o, a kąt rozwarty drugiego rombu ma miarę 115o
boki tych rombów są proporcjonalne
kąty rozwarte tych rombów są równe
7. Długości boków prostokąta są równe 2cm i 5cm. Oblicz wymiary prostokąta
podobnego, którego obwód jest równy 56cm.
8. W trójkącie ABC odcinek ED jest równoległy do boku CA(rys.). Oblicz długość
odcinka BE.
9. Sprawdź czy proste BD i CE są równoległe, jeżeli: /AB/ = 3,25cm, /AD/ = 6,5cm,
/BC/ = 0,25dm, /DE/ = 0,05m
10. W trójkącie ABC odcinek KL łączy środki boków AC i BC. Ile razy boki trójkąta
KLC są mniejsze od odpowiednich boków trójkąta ABC? Odpowiedź uzasadnij.