mgr inż. Barbara Tobiasz Prawa autorskie zastrzeżone

Karta pracy
IMIĘ I NAZWISKO……………………… KLASA….
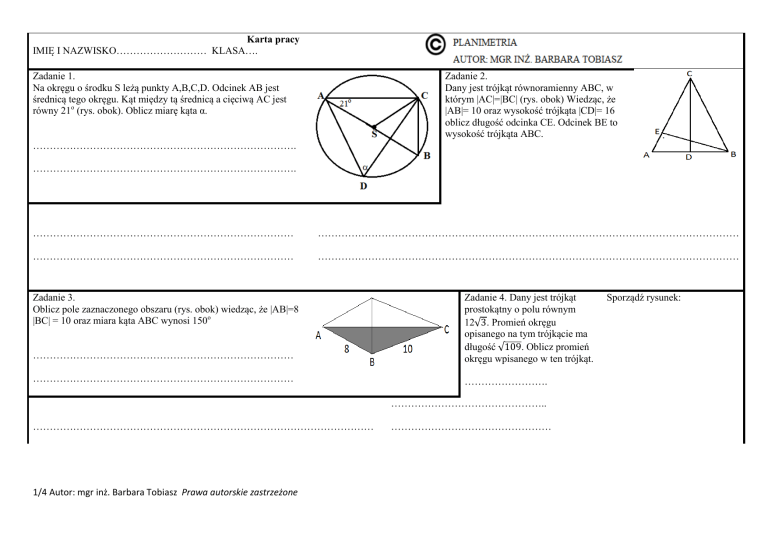
Zadanie 1.
Na okręgu o środku S leżą punkty A,B,C,D. Odcinek AB jest
średnicą tego okręgu. Kąt między tą średnicą a cięciwą AC jest
równy 21o (rys. obok). Oblicz miarę kąta α.
Zadanie 2.
Dany jest trójkąt równoramienny ABC, w
którym |AC|=|BC| (rys. obok) Wiedząc, że
|AB|= 10 oraz wysokość trójkąta |CD|= 16
oblicz długość odcinka CE. Odcinek BE to
wysokość trójkąta ABC.
…………………………………………………………………….
…………………………………………………………………….
……………………………………………………………………
………………………………………………………………………………………………………………
……………………………………………………………………
………………………………………………………………………………………………………………
Zadanie 3.
Oblicz pole zaznaczonego obszaru (rys. obok) wiedząc, że |AB|=8
|BC| = 10 oraz miara kąta ABC wynosi 150o
……………………………………………………………………
Zadanie 4. Dany jest trójkąt
prostokątny o polu równym
12 . Promień okręgu
opisanego na tym trójkącie ma
długość
. Oblicz promień
okręgu wpisanego w ten trójkąt.
……………………………………………………………………
…………………….
………………………………………..
…………………………………………………………………………………………
1/4 Autor: mgr inż. Barbara Tobiasz Prawa autorskie zastrzeżone
…………………………………………
Sporządź rysunek:
Zadanie 5. Oblicz promień okręgu opisanego na trójkącie równobocznym o boku długości 4
…………………
Sporządź rysunek:
………………………………………………………………………………………………………………………………..
…………………………………………………………………………………………………………………………………
Zadanie 6. Przez środek okręgu poprowadzono prostą k, która na okręgu wyznaczyła punkty A i B następnie odmierzono kąt BAC o mierze równej 58o . Przez wierzchołek C
poprowadzono styczną do okręgu przecinającą prostą k w punkcie D. Oblicz miary kątów trójkąta ACD.
Sporządź rysunek:
………………………………………………………………………………………………………………………………
Zadanie 7. Oblicz odległość środków okręgów stycznych
zewnętrznie wiedząc, że punkty A i B to punkty
styczności stycznej do obu okręgów oraz |AB|=12 i
promień mniejszego okręgu ma długość równą 4.(rys.)
Zadanie 8. Obwód rombu jest równy 4
a suma
długości jego przekątnych wynosi 22 . Oblicz długość
wysokości tego rombu.
Sporządź rysunek:
……………………
………………………………………………………….
…………………….
………………………………………………………….
................................
Zadanie 9. Punkt S jest środkiem okręgu opisanego na trójkącie
ostrokątnym ABC. Kąt ACS jest trzy razy większy od kąta BAS, a kąt
CBS jest dwa razy większy od kąta BAS. Oblicz miary kątów w trójkącie
ABC. (rys. obok)
……………………
……………………
……………………………………………………….
…………………………………………………………………………….
……………………………………………………….
…………………………………………………………………………….
……………………………………………………….
…………………………………………………………………………….
……………………………………………………….
2/4 Autor: mgr inż. Barbara Tobiasz Prawa autorskie zastrzeżone
Zadanie 10. W okrąg o promieniu 12 wpisano trójkąt prostokątny. Oblicz pole tego trójkąta, gdy sinus jednego z kątów jest równy 0,6.
Sporządź rysunek:
………………………………………………………………………………………………………………………….
………………………………………………………………………………………………………………………….
Zadanie 11. Oblicz pole trójkąta równobocznego, którego długość promienia
okręgu wpisanego w ten trójkąt jest równa 25
Sporządź rysunek:
……………………………………………………………………………………………………………………………..
……………………………………………………………………………………………………………………………..
Zadanie 12. Dany jest kwadrat ABCD. Oblicz miarę kąta  przedstawionego na
rysunku.
Zadanie 13. Przekątne równoległoboku o długościach
odpowiednio 12 i 8 przecinają się pod kątem 60. Oblicz
pole tego równoległoboku.
………………………………………………………………………………………………………………………
Sporządź rysunek:
…………………………………………
………………………………………………………………………………………………………………………
………………………………………..
…………………………………………
…………………………………………
Zadanie 14. W trapezie równoramiennym o obwodzie 56 cm przekątna jest
dwusieczną kąta ostrego, a stosunek długości krótszej podstawy do dłuższej jest
równy 1 : 2. Oblicz długości boków trapezu.
………………………………………………………………………………………………………………………….
3/4 Autor: mgr inż. Barbara Tobiasz Prawa autorskie zastrzeżone
Sporządź rysunek:
Zadanie 15. W okręgu o środku O dany jest kąt wpisany BAC o
mierze 29o. Styczne do okręgu w punktach B i C przecinają się w
punkcie D. Oblicz miarę kąta BDC.
Sporządź rysunek:
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
Zadanie 16. Dany jest okrąg o środku S (rys.)Oblicz miarę kąta 
przedstawionego na rysunku.
Zadanie 17. Dwa wielokąty są podobne w skali 1: 5. Pole jednego z nich
jest równe 17 cm2. Oblicz pole drugiego wielokąta.
…………………………………………………………………………………………………….
………………………………………………………………
…………………………………………………………………………………………………….
………………………………………………………………
Zadanie 18. Dany jest trapez równoramienny ABCD o podstawach
długości 18 i 14 i ramieniu długości 8. Punkt S to punkt przecięcia
przedłużonych ramion trapezu (rys.) Oblicz obwód trójkąta ABS.
…………………………………………………………………………………………………….
Zadanie 19. Stosunek pola trójkąta do pola koła wpisanego w ten trójkąt
jest równy 3:π. Wiedząc, że średnica koła ma długość 6 cm, oblicz obwód
trójkąta.
Sporządź rysunek:
…………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………….
Zadanie 20. Odcinek CD jest środkową w trójkącie ABC. Trójkąt DBC
ma pole równe 3 cm2. Oblicz pole trójkąta ABC.
………………………………………………………………………………………………………
4/4 Autor: mgr inż. Barbara Tobiasz Prawa autorskie zastrzeżone
Sporządź rysunek:
Zadanie 21. Kąt wpisany w koło ma miarę równą 30o i jest oparty na łuku
długości 4π. Oblicz pole wycinka koła, wyznaczonego przez ten sam łuk.
Sporządź rysunek:
…………………………………………………………