Teoria w pigu³ce Dlaczego s³uszne jest prawo Ohma

Dlaczego s³uszne jest prawo Ohma
Teoria w pigu³ce
Dlaczego s³uszne jest prawo Ohma
Karol Œwierc
U
W niniejszym numerze rozpoczynamy cykl problemów prezentowanych w nowej rubryce „Teoria w
pigu³ce”. Zgodnie z za³o¿eniem bêd¹ to krótkie problemy teoretyczne rozpatrzone z wiêksz¹ wnikliwoœci¹
ani¿eli czynimy to w artyku³ach prezentowanych w
naszym piœmie. Pomimo to, chcemy zachowaæ niewielk¹ i nie mêcz¹c¹ objêtoœæ tej rubryki. Problemy tu
rozpatrywane bêd¹ zatem sprecyzowane bardzo w¹sko.
E
I
vt
vu
l
Prawo Ohma. Czy istnieje prawo prostsze? Pr¹d proporcjonalny do napiêcia. Dlaczego mia³o by byæ inaczej dla najprostszych przewodników, dla rezystorów, materia³ów dobrze
lub gorzej przewodz¹cych pr¹d, ale liniowych? Jak siê bli¿ej
przyjrzeæ mechanizmowi przewodnictwa elektrycznego, okazuje siê, ¿e prawo Ohma nie jest bynajmniej oczywiste. Przyjrzyjmy siê zatem temu mechanizmowi.
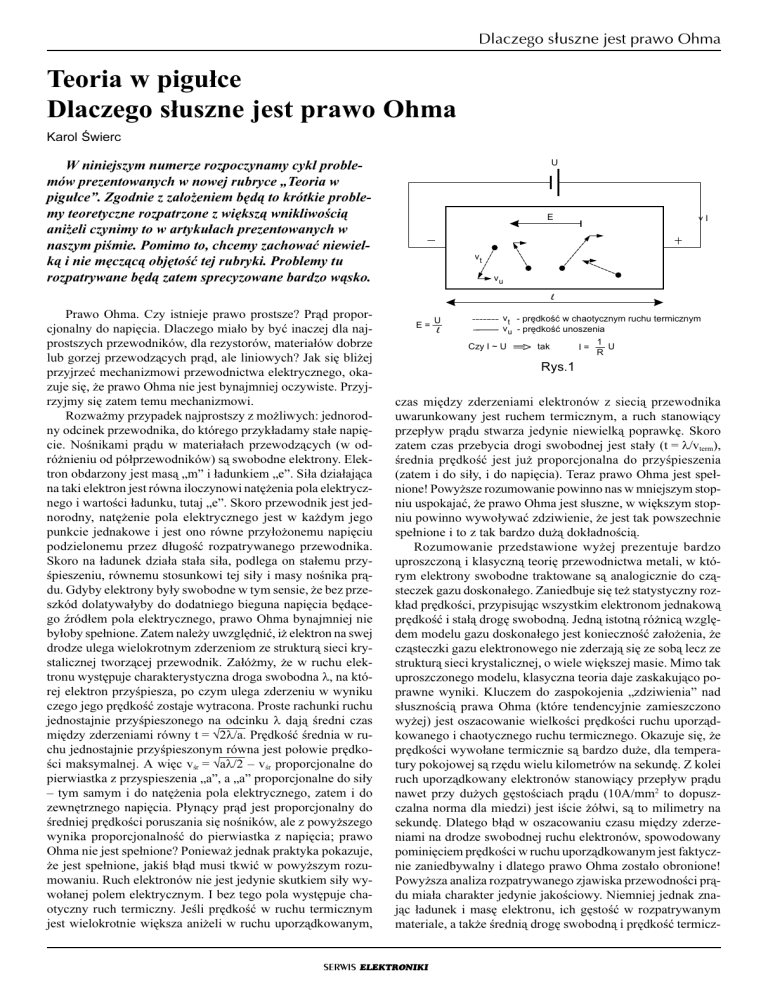
Rozwa¿my przypadek najprostszy z mo¿liwych: jednorodny odcinek przewodnika, do którego przyk³adamy sta³e napiêcie. Noœnikami pr¹du w materia³ach przewodz¹cych (w odró¿nieniu od pó³przewodników) s¹ swobodne elektrony. Elektron obdarzony jest mas¹ „m” i ³adunkiem „e”. Si³a dzia³aj¹ca
na taki elektron jest równa iloczynowi natê¿enia pola elektrycznego i wartoœci ³adunku, tutaj „e”. Skoro przewodnik jest jednorodny, natê¿enie pola elektrycznego jest w ka¿dym jego
punkcie jednakowe i jest ono równe przy³o¿onemu napiêciu
podzielonemu przez d³ugoœæ rozpatrywanego przewodnika.
Skoro na ³adunek dzia³a sta³a si³a, podlega on sta³emu przyœpieszeniu, równemu stosunkowi tej si³y i masy noœnika pr¹du. Gdyby elektrony by³y swobodne w tym sensie, ¿e bez przeszkód dolatywa³yby do dodatniego bieguna napiêcia bêd¹cego Ÿród³em pola elektrycznego, prawo Ohma bynajmniej nie
by³oby spe³nione. Zatem nale¿y uwzglêdniæ, i¿ elektron na swej
drodze ulega wielokrotnym zderzeniom ze struktur¹ sieci krystalicznej tworz¹cej przewodnik. Za³ó¿my, ¿e w ruchu elektronu wystêpuje charakterystyczna droga swobodna λ, na której elektron przyœpiesza, po czym ulega zderzeniu w wyniku
czego jego prêdkoœæ zostaje wytracona. Proste rachunki ruchu
jednostajnie przyœpieszonego na odcinku λ daj¹ œredni czas
miêdzy zderzeniami równy t = √2λ/a. Prêdkoœæ œrednia w ruchu jednostajnie przyœpieszonym równa jest po³owie prêdkoœci maksymalnej. A wiêc vœr = √aλ/2 – vœr proporcjonalne do
pierwiastka z przyspieszenia „a”, a „a” proporcjonalne do si³y
– tym samym i do natê¿enia pola elektrycznego, zatem i do
zewnêtrznego napiêcia. P³yn¹cy pr¹d jest proporcjonalny do
œredniej prêdkoœci poruszania siê noœników, ale z powy¿szego
wynika proporcjonalnoœæ do pierwiastka z napiêcia; prawo
Ohma nie jest spe³nione? Poniewa¿ jednak praktyka pokazuje,
¿e jest spe³nione, jakiœ b³¹d musi tkwiæ w powy¿szym rozumowaniu. Ruch elektronów nie jest jedynie skutkiem si³y wywo³anej polem elektrycznym. I bez tego pola wystêpuje chaotyczny ruch termiczny. Jeœli prêdkoœæ w ruchu termicznym
jest wielokrotnie wiêksza ani¿eli w ruchu uporz¹dkowanym,
E=
U
l
v t - prêdkoœæ w chaotycznym ruchu termicznym
v u - prêdkoœæ unoszenia
Czy I ~ U
tak
I=
1
U
R
Rys.1
czas miêdzy zderzeniami elektronów z sieci¹ przewodnika
uwarunkowany jest ruchem termicznym, a ruch stanowi¹cy
przep³yw pr¹du stwarza jedynie niewielk¹ poprawkê. Skoro
zatem czas przebycia drogi swobodnej jest sta³y (t = λ/vterm),
œrednia prêdkoœæ jest ju¿ proporcjonalna do przyœpieszenia
(zatem i do si³y, i do napiêcia). Teraz prawo Ohma jest spe³nione! Powy¿sze rozumowanie powinno nas w mniejszym stopniu uspokajaæ, ¿e prawo Ohma jest s³uszne, w wiêkszym stopniu powinno wywo³ywaæ zdziwienie, ¿e jest tak powszechnie
spe³nione i to z tak bardzo du¿¹ dok³adnoœci¹.
Rozumowanie przedstawione wy¿ej prezentuje bardzo
uproszczon¹ i klasyczn¹ teoriê przewodnictwa metali, w którym elektrony swobodne traktowane s¹ analogicznie do cz¹steczek gazu doskona³ego. Zaniedbuje siê te¿ statystyczny rozk³ad prêdkoœci, przypisuj¹c wszystkim elektronom jednakow¹
prêdkoœæ i sta³¹ drogê swobodn¹. Jedn¹ istotn¹ ró¿nic¹ wzglêdem modelu gazu doskona³ego jest koniecznoœæ za³o¿enia, ¿e
cz¹steczki gazu elektronowego nie zderzaj¹ siê ze sob¹ lecz ze
struktur¹ sieci krystalicznej, o wiele wiêkszej masie. Mimo tak
uproszczonego modelu, klasyczna teoria daje zaskakuj¹co poprawne wyniki. Kluczem do zaspokojenia „zdziwienia” nad
s³usznoœci¹ prawa Ohma (które tendencyjnie zamieszczono
wy¿ej) jest oszacowanie wielkoœci prêdkoœci ruchu uporz¹dkowanego i chaotycznego ruchu termicznego. Okazuje siê, ¿e
prêdkoœci wywo³ane termicznie s¹ bardzo du¿e, dla temperatury pokojowej s¹ rzêdu wielu kilometrów na sekundê. Z kolei
ruch uporz¹dkowany elektronów stanowi¹cy przep³yw pr¹du
nawet przy du¿ych gêstoœciach pr¹du (10A/mm2 to dopuszczalna norma dla miedzi) jest iœcie ¿ó³wi, s¹ to milimetry na
sekundê. Dlatego b³¹d w oszacowaniu czasu miêdzy zderzeniami na drodze swobodnej ruchu elektronów, spowodowany
pominiêciem prêdkoœci w ruchu uporz¹dkowanym jest faktycznie zaniedbywalny i dlatego prawo Ohma zosta³o obronione!
Powy¿sza analiza rozpatrywanego zjawiska przewodnoœci pr¹du mia³a charakter jedynie jakoœciowy. Niemniej jednak znaj¹c ³adunek i masê elektronu, ich gêstoœæ w rozpatrywanym
materiale, a tak¿e œredni¹ drogê swobodn¹ i prêdkoœæ termicz-
SERWIS ELEKTRONIKI
Dlaczego s³uszne jest prawo Ohma
n¹ „gazu elektronowego” mo¿na pokusiæ siê o obliczenie opornoœci w³aœciwej lub jak fizycy wol¹ przewodnoœci materia³u.
O dziwo, wyniki s¹ bardzo bliskie wartoœci potwierdzonych
doœwiadczalnie. Nale¿y jednak przyznaæ, ¿e s¹ odstêpstwa co
do zale¿noœci rezystancji w³aœciwej od temperatury. Tak¿e niektóre zgodnoœci teorii klasycznej s¹ jedynie dzie³em przypadku. Pe³ne wyjaœnienie zjawisk daje dopiero teoria kwantowa.
Niby elementarna sprawa, a zjawisko ciekawe. O wiele
bardziej zaskakuj¹ce s¹ inne zjawiska w po³¹czeniu z faktem,
¿e prêdkoœci (uporz¹dkowane) noœników pr¹du s¹ tak mizerne. W fizyce dobrze znane jest zjawisko, i¿ przep³yw pr¹du
wytwarza pole magnetyczne. Znane jest te¿ to, ¿e pole magnetyczne jest w istocie relatywistycznym efektem ruchu noœników pr¹du. Efekt relatywistyczny przy prêdkoœci ¿ó³wia lub
œlimaka? Okazuje siê, ¿e tak. Parê s³ów na uzasadnienie tego
nader ciekawego efektu podamy w innym numerze „SE” w
k¹ciku „Teoria w pigu³ce”.
}
SERWIS ELEKTRONIKI