Wykład III. Dyfrakcja promieni Rentgena
Oddziaływanie fali elektromagnetycznej z kryształem zależy od długości fali. Odległości pomiędzy
atomami w sieci krystalicznej wynoszą ok. 2- 3 Ǻ. Tego samego rzędu są też odległości pomiędzy
płaszczyznami sieciowymi. Jest to znacznie mniej niż wynosi długość fali światła widzialnego 4000-8000 Ǻ.
Powoduje to, że oddziaływanie światła z kryształem nie powinno zależeć bezpośrednio od struktury
krystalicznej. Mówiąc inaczej, ponieważ długość fali światła jest dużo większa niż odległości międzyatomowe
większość efektów, które obserwujemy przy przejściu światła przez kryształ nie jest związana bezpośrednio z
jego strukturą (np załamanie światła czy odbicie w ośrodkach izotropowych), zaś wielkości fizyczne, które
opisują taki proces są wielkościami makroskopowymi.
Inaczej jest gdy mamy do czynienia z bardzo krótkimi falami elektromagnetycznymi. Wówczas
periodyczność kryształu powoduje, że w stosunku do fali elektromagnetycznej o długości krótszej niż odległości
pomiędzy płaszczyznami sieciowymi, działa on podobnie jak siatka dyfrakcyjna dla światła widzialnego. Gdy
oświetlimy kryształ promieniami Rentgena, których długość fali jest ok 0.1 do 1 Ǻ, promienie te będą
interferować pomiędzy sobą tworząc po przejściu przez kryształ obraz dyfrakcyjny. Zjawisko to zostało
szeroko wykorzystane w krystalografii do określania własności geometrycznych sieci krystalicznych.
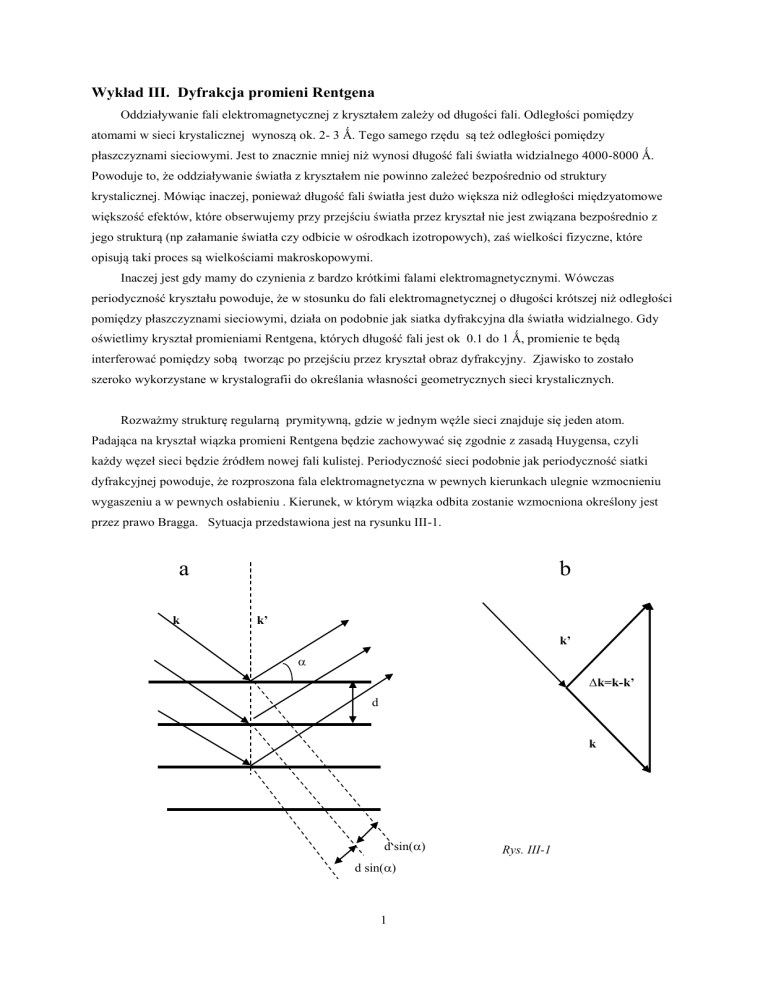
Rozważmy strukturę regularną prymitywną, gdzie w jednym węźle sieci znajduje się jeden atom.
Padająca na kryształ wiązka promieni Rentgena będzie zachowywać się zgodnie z zasadą Huygensa, czyli
każdy węzeł sieci będzie źródłem nowej fali kulistej. Periodyczność sieci podobnie jak periodyczność siatki
dyfrakcyjnej powoduje, że rozproszona fala elektromagnetyczna w pewnych kierunkach ulegnie wzmocnieniu
wygaszeniu a w pewnych osłabieniu . Kierunek, w którym wiązka odbita zostanie wzmocniona określony jest
przez prawo Bragga. Sytuacja przedstawiona jest na rysunku III-1.
a
k
b
k’
k’
Δk=k-k’
d
k
d sin()
d sin()
1
Rys. III-1
Promienie Rentgena padające na kryształ pod kątem ulegają odbiciu od poszczególnych płaszczyzn
sieciowych odległych od siebie o d. Jeśli różnica dróg optycznych będzie równa całkowitej wielokrotności
długości fali nastąpi wzmocnienie. Warunek ten można opisać wzorem, który nosi nazwę prawa Bargga:
2d sin n
(III-1)
d jest odległością pomiędzy płaszczyznami a długością fali.
Rys III-2 Różne płaszczyzny
sieciowe
Ze względów historycznych kąt ugięcia nie jest liczony względem normalnej a względem powierzchni
płaszczyzny sieciowej. Ponieważ w krysztale istnieje wiele płaszczyzn sieciowych rozpraszających
promieniowanie elektromagnetyczne wiązka padająca uginać się będzie pod różnymi kątami. Każdej wiązce
ugiętej odpowiadać będzie inna rodzina płaszczyzn. Ponieważ poszczególne wiązki są jednoznacznie
przyporządkowane płaszczyznom sieciowym można je identyfikować przy pomocy wskaźników Millera.
Prawo Bragga można przedstawić również w innej postaci. Rysunek III-1 b w sposób graficzny
przedstawia prawo zachowania pędu przy zjawisku odbicia promieniowania rentgenowskiego od kryształu.
Korzystając z faktu, że wektor falowy, k, jest związany z długością fali następującą relacją
k
2
(III-2)
oraz z relacji (III-1) zauważamy :
2 2
Δk=|k-k’| = 2 k sinα =
sinα
(III-3)
Wobec powyższego musi być spełniony warunek
k
2
d
(III-4)
2π/d jest długością wektora sieci odwrotnej, G. Relacje (III-3) i (III-4) prowadzą bezpośrednio do
następującego równania:
k-k’=G
(III-5)
gdzie G jest wektorem sieci odwrotnej , prostopadłym do rodziny płaszczyzn od której odbija się wiązka
promieni Rentgena. Równanie (III-5) jest całkowicie równoważne równaniu (III-1).
2
Warunek Bragga wyrażony przy pomocy relacji (III-1) lub (III-5) pozwala wyłącznie na jakościową
analizę dyfrakcji promieni Rentgena na kryształach, czyli dla danej struktury pozwala na określenie możliwych
kątów ugięcia. W krystalografii do określania struktury krystalicznej ważne jest także przewidywanie natężeń
poszczególnych wiązek. W celu analizy natężenia wiązki odbitej rozważmy rysunek. (III-3).
Rysunek III-3
k’
r
R
k
Na rysunku każdy punkt odpowiada węzłowi sieci krystalicznej. Linie przerywane to czoło fali
promieniowania rentgenowskiego. Zgodnie z zasadą Huygensa każdy węzeł sieci staje się źródłem nowej fali
kulistej . Zgodnie z zasadami elektrodynamiki klasycznej amplituda promieniowania rozproszonego na węźle ,
mierzona w odległości r od węzła jest równa:
F()= F0 exp(-ik)
exp( ik ' r )
r
(III-6)
W eksponencie, w mianowniku iloczyn skalarny k’r= k’r ponieważ fala ugięta jest fala kulistą. F0 jest amplitudą
fali padającej. Elementarne przekształcenia geometryczne ( patrz rysunek III-3) pozwalają na użycie
przybliżenia:
r |R-| = R 2 2 2R cos R cos
(III-7)
Podstawiając (III-7) do (III-6)
F()=F0
exp(-ikR)
exp{-i [k-k cos]}
R
(III-8)
Uwzględniając, że dla małych kryształów, gdy punkt obserwacji znajduje się daleko od kryształu, każdy wektor
r jest w przybliżeniu równoległy do R, definiuje się wektor k’, który jest wektorem falowym fali rozproszonej
(patrz rys III-3) taki że |k’|=k oraz
k cos = k’
(III-9)
i
3
F (ρ)=F0
exp(-ikR)
exp(-ikR)
exp{-i [k-k’]} = F0
exp{-i [∆k]}
R
R
(III-10)
Tak jest w przypadku sieci z bazą jednoatomową. Jeśli baza składa się z więcej niż jednego atomu musimy brać
pod uwagę sumę amplitud od wszystkich atomów w komórce elementarnej. Odpowiednia sumaryczna
amplituda w położeniu R, fal wyemitowanych w komórce, w położeniu , będzie równa;
F (ρ)= F0
= F0
exp(-ikR)
R
f
j
exp{-i [+rj]∆k}
j
exp(-ikR)
exp{-i [∆k]}
R
f
j
exp{-i rj∆k}
(III-11)
j
gdzie rj jest położeniem j-tego atomu w komórce elementarnej. Ostatnia suma we wzorze (III-11) nosi nazwę
czynnika struktury.
Dla każdego odbitego promienia czynnik strukturalny można obliczyć następująco.
Załóżmy , że odbicie następuje od płaszczyzny oznaczonej wskaźnikami Millera hkl. Wówczas
∆k=Ghkl=hg1+kg2+lg3. Położenie j-tego atomu w komórce jest określone przez wektor rj=uj a1+ vja2 +wja3,
gzie u ,v, w są zerami lub liczbami ułamkowymi. Łatwo obliczyć, że
rj*Ghkl=2π(ujh+vjk+wjl)
(III-12)
Korzystając z relacji (III-12) otrzymuje się następujące wyrażenie na czynnik struktury
hkl f j exp{ i 2 (u j h v j k w j l)}
(III-13)
j
We wzorach (III-11) i (III-13) fj jest czynnikiem atomowym, który zależy od zdolności rozpraszania
promieni rentgena przez dany atom. Zakładając, że to elektrony są odpowiedzialne za rozpraszanie promieni
rentgena jest on równy ilości elektronów w atomie. Istotna jest również gęstość atomów w danej płaszczyźnie
sieciowej. Czynnik atomowy powinien być proporcjonalny do tej wielkości.
Aby otrzymać całkowitą amplitudę w punkcie R należy posumować amplitudy (III-10) po wszystkich
komórkach elementarnych. Ponieważ czynnik struktury jest identyczny dla każdej komórki elementarnej
możemy wyłączyć go z sumowania. To samo dotyczy stałego czynnika zależnego od R.
Korzystając z faktu, że ρ jest wektorem translacji sieci prostej
ρ = na1+ma2 +pa3
(III-14)
sumowanie po komórkach elementarnych zastępujemy sumowaniem po n,m, p
4
F=
F (ρ) =
exp(-ikR)
{ exp [-in(a1∆k)]} { exp [-im(a2∆k)]} { exp [-ip(a3∆k)]} (IIIR
p
n
m
15)
Dla skończonych kryształów zawierających np. M komórek elementarnych , każda z powyższych sum jest
równa
M
exp [-in(a1∆k)]=
m 1
1 exp[ iM (a1k )]
1 exp[ i(a1k )]
(III-16)
Do tej pory obliczyliśmy wypadkowe amplitudy promieniowania rentgenowskiego rozproszonego na krysztale .
Pamiętać jednak należy, że to co na prawdę możemy zarejestrować to natężenie promieniowania, I.
Zgodnie z klasyczną definicją
I F * F
(III-17)
gdzie F* jest amplitudą sprzężoną do F. Korzystając z równości
1
sin 2 [ M (a 1 k )]
1 exp[ iM (a1k )] 1 exp[ iM (a1k )]
2
=
1
1 exp[ i(a1k )] 1 exp[ i(a1k )]
sin 2 ( a 1 k )
2
(III-18)
otrzymamy następujące wyrażenie na natężenie promienia odbitego od danej płaszczyzny
1
1
1
sin 2 [ M (a1k )] sin 2 [ M (a 2 k )] sin 2 [ M (a3k )]
2
2
2
I (k )
. (III-19)
1
1
R
2
2
2 1
sin ( a1k )
sin ( a 2 k )
sin ( a3k )
2
2
2
2
hkl
2
gdzie Λhkl jest czynnikiem struktury. Łatwo zauważyć, że poprzednie założenie że ∆k jest równe wektorowi
sieci odwrotnej, ∆k=Ghkl , pociągając za sobą :
aj Ghkl = n2π
(III-20)
8k
2 .
dla j=1,2,3 daje maksimum funkcji (III-19). Wykres (III-4) przedstawia funkcję
k
sin 2
2
sin 2
Łatwo zaważyć ,że główne maxima pojawiają się gdy wektor falowy jest wielokrotnością liczby . Wielkość
bocznych maksimów zmniejsza się bardzo gdy mamy do czynienia z większą liczbą węzłów. W praktyce są one
niewidoczne dla M większych od 100. W warunkach normalnych mamy do czynienia z kryształami
składającymi się z 1020 atomów.
5
Rys III-4. Obraz dyfrakcyjny
otrzymany dla sieci składającej się z
8 węzłów
Przykłady dyfrakcji.
Promieniowanie rentgenowskie jest promieniowaniem elektromagnetycznym o długości fal od 0.1 do kilku Å.
Do wytwarzania promieni rentgena służą specjalne lampy elektronowe, w których rozpędzone w polu
elektrostatycznym elektrony uderzają w metalową antykatodę. Podczas tych zderzeń elektron traci energię w
skutek dwóch niezależnych procesów. Pierwszy z nich to hamowanie w polu elektrycznym atomów antykatody .
Drugi to wzbudzenie elektronów rdzeni atomowych atomów antykatody. Oba procesy powodują pojawienie
się wysokoenergetycznych fotonów . Pierwszy to rodzaj promieniowania Czerenkowa dający ciągłe widmo
promieniowania ( promieniowanie hamowania). W drugim procesie pobudzone atomy wracając do stanu
podstawowego wysyłają kwanty promieniowania rentgenowskiego. Widmowy rozkład tych fotonów ma
charakter dyskretny i zależy od materiału antykatody. Promieniowanie to nosi nazwę promieniowania
charakterystycznego. Różne metody wykorzystują różne zakresy widma promieniowania rentgenowskiego.
1. Metoda Lauego
Wiązka promieniowania ciągłego pada na monokryształ. Ponieważ wiązka zawiera różne długości fal
otrzymamy wiele wiązek odbitych. Można założyć, że każda płaszczyzna znajdzie odpowiadającą jej długość
fali, która ulegnie wzmocnieniu dla danego kąta padania. Rysunek III. 5 a i III-5 b
6
Rys III.5
a
Każdemu odbiciu odpowiada
widmo ciągłe
inna długość fali
b
widmo ciągłe
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
λ120
(210)
λ210
(120)
λ110
(110)
W ten sposób refleksy otrzymane na ekranie będą odpowiadały wszystkim płaszczyznom sieciowym.
Przykładowy obraz dyfrakcji Lauego przedstawiony jest na rysunku. III-6
Rysunek III-6. Lauerogram kryształu krzemu.
Obraz jest w przybliżeniu niezmieniony przy
obrocie o kąt 2π/4. Wynika to z istnieniem osi
obrotu o kąt 2π/4 kryształu krzemu.( oś [100]) .
Uwaga : osie krystalograficzne oznaczmy wskaźnikami Millera w nawiasach kwadratowych
2. Metoda obracanego kryształu
7
W metodzie Lauego uzyskiwaliśmy odbicia od więcej niż jednej płaszczyzny krystalograficznej ponieważ
oświetlaliśmy kryształu wiązką o widmie ciągłym. W metodzie obracanego kryształu oświetlamy kryształ
wiązką monochromatyczną. W układzie takim odbicie otrzymuje się tylko od określonej płaszczyzny ( h k l )
dla której spełniony jest warunek Bragga,
2d hkl sin hkl .
(III-21)
Dlatego też, aby otrzymać więcej odbić, oświetlana próbka wprawiana jest w ruch obrotowy wokół osi
prostopadłej do wiązki. W ten sposób zmieniając kąt nachylenia płaszczyzny α możemy dla tej samej długości
fali spełnić warunek (III-21) dla kilku różnych płaszczyzn i otrzymać kilka wiązek odbitych pod różnymi
kontami. Aparatura do badania kryształów metodą obracanego kryształu przedstawiona jest na rysunku
III -7.
Rys III-7 komora do dyfrakcji metodą obracanego kryształu
W metodzie tej podobnie jak w metodzie Lauego każdej płaszczyźnie odpowiada refleks punktowy.
3. Metoda proszkowa.
Bardziej uniwersalna jest metoda proszkowa. I w tym przypadku używamy wiązki monochromatycznej .
Zamiast monokryształu stosuje się jednak proszek krystaliczny, który umieszcza się w rurce kapilarnej. Ziarna
proszku ustawione są zupełnie przypadkowo. Padająca wiązka odbija się tylko od tych ziaren , których
płaszczyzny sieciowe ustawione osą pod odpowiednim kątem. Ze względu na całkowicie przypadkowe
ustawienie kryształów w proszku ( w odróżnieniu od metody obracanego kryształu układ nie ma symetrii
osiowej, związanej z kryształem ) wiązki odbite mają kształt stożków. Dla sieci regularnej kąty tych stożków
zależą od stałej sieci a, wartości wskaźników Millera hkl oraz długości fali, λ, w następujący sposób
8
sin
h2 k 2 l 2
(III-22
2a
Komora do badania kryształów metodą proszkową przedstawiona jest na rysunku III –8
Rys. III-8 a) Komora proszkowa.,
b) rysunek schematyczny
9
We wszystkich wyżej wspomnianych przypadkach detekcja promieniowania odbitego może odbywać się
poprzez zaczernienie kliszy fotograficznej. Bardziej nowoczesna metoda polega na bezpośredniej detekcji
promieniowania rentgenowskiego. Ze względu na dużą przenikliwość promieniowania rentgenowskiego , jego
bezpośrednia detekcja nie jest wcale sprawą prostą Na ogół używa się do tego celu specjalnych detektorów,
działających w oparciu o zjawisko scyntylacji. Przykład detektor przedstawiony jest na rysunku III-9
Rysunek III-9 Układ detektora promieniowania rentgenowskiego
Promieniowanie
rentgenowskie
scyntyla
tor
fotopowielacz
Promieniowanie rentgena pochłaniane jest przez kryształ- scyntylator, który z kolei pod wpływem takiego
wzbudzenia emituje kwanty światła widzialnego ( proces ten nazywamy scyntylacją). Kwanty światła
rejestrowane są przez fotopowielacz lub inne urządzenie np. fotodiodę.
Inne metody analizy struktury krystalograficznej
Jak przedstawiono powyżej do badań struktury krystalograficznej można użyć promieniowania
elektromagnetycznego ( promieniowania rentgena). W ostatnich dziesięcioleciach rozwinęły się również inne
metody badań oparte na dyfrakcji elektronów , neutronów i lekkich atomów. Zjawisko dyfrakcji cząstek
materialnych na kryształach związane jest z falowa naturą materii. Zgodnie z zasadą pierwszej kwantyzacji
każdej cząstce przyporządkowuje się falę o długości:
2
p
(III.23)
gdzie p jest pędem cząstki a stałą Plancka podzieloną przez 2
.
Odpowiada to funkcji falowej cząstki
swobodnej będącej falą płaską daną wzorem:
e ikr
(III.24)
gdzie wektor falowy k związany jest z pędem cząstki następującą relacją: p k . Podobnie jak w przypadku
dyfrakcji promieni rentgena, aby zaszła dyfrakcja elektronów, neutronów lub atomów, fala materii musi spełniać
warunek Bragga (III.1) lub (III.5). Stosowane metody eksperymentalne są bardzo podobne lub analogiczne do
metod używanych w dyfrakcji promieni rentgena. Zależność długości fali od energii dla poszczególnych
cząstek przedstawia rysunek III.9
10
Rys III.9 Długość fali
deBroglie’a fotonów ,
elektronów , neutronów i
atomów helu w funkcji
energii. Strzałka wskazuje
energię termiczną cząstek
energia (keV)
1.
Dyfrakcja elektronów
. Technika doświadczalna dyfrakcji elektronów nosi skrótową nazwę LEED, od angielskiego terminu Low
Energy Electron Difraction. Do badania struktury krystalicznej używa się wiązki elektronów o energii od 10 do
1000 eV. Wiązka elektronów jest bardzo silnie rozpraszana przez ciało stałe, stąd głębokość penetracji nie
przekracza kilku lub kilkunastu stałych sieci. Ogranicza to stosowanie metody LEED tylko do badania wiązki
odbitej, zaś informacje uzyskane dotyczą tylko struktury warstwy powierzchniowej materiału. Duża trudność
doświadczalną stanowi konieczność uzyskania ultra wysokiej próżni, rzędu 10 -9 Tr , niezbędnej do zachowania
odpowiednio długiej drogi swobodnej elektronów w całym układzie pomiarowym. Schemat układu
doświadczalnego przedstawiony jest na rysunku (III.10). Uzyskiwane obrazy dyfrakcyjne są bardzo podobne do
tych otrzymanych w metodzie Lauego.
Rys.III 10 Schemat układu do
badania dyfrakcji elektronów
o niskiej energii (LEED).
11
2.
Wiązki neutronów
Skonstruowanie reaktorów jądrowych wytwarzających wiązki neutronów o dużym natężeniu pozwoliło na
ich wykorzystanie do badań struktury krystalicznej. Większość wytwarzanych w reaktorach neutronów to
tzw. neutrony termiczne, o energii kinetycznej odpowiadającej temperaturze T=400K Odpowiadająca im
długość fali wynosi kilka Å ( patrz rysunek III.9). Precyzyjne wyselekcjonowanie neutronów o dobrze
określonej energii odbywa się za pomocą monochromatora krystalicznego, którego działanie tak jest
analogiczne do działania siatki dyfrakcyjnej wobec promieniowania widzialnego. Otrzymane w ten sposób
monochromatyczne neutrony wykorzystuje się w neutronowej metodzie Debey’a -Sherrera lub w metodzie
obracanego kryształu. Wiązkę neutronów stosuje się przede wszystkim do badania uporządkowania
magnetycznego, badania przejść fazowych ( porządek- nieporządek) oraz położeń atomów wodoru w
ciałach stałych, cząsteczkach i układach biologicznych.
3.
Wiązki atomów.
Prowadzono również badania dyfrakcji atomów helu i cząsteczek wodoru na kryształach. Obiekty takie
praktycznie nie wchodzą do wnętrza materiału, dlatego też obrazy dyfrakcyjne otrzymywane metodą
wiązek atomowych odwzorowują strukturę powierzchni nie związaną z położeniami poszczególnych
atomów tylko z mniej lub bardziej regularnymi uskokami o wysokości jednej warstwy atomowej.
12










