Doświadczalnictwo leśne
Wydział Leśny SGGW
Studia II stopnia
Wykład 8
• Rozkłady statystyczne
– Rozkłady empiryczne
– Po co rozkłady?
– Typy zmiennych
– Przykładowe rozkłady
• Rozkład normalny
• Rozkład dwumianowy
Rozkłady empiryczne
• Graficzna reprezentacja danych w formie
rozkłady liczebnosci, wieloboku
liczebności, histogramu, itp.
Graficzna prezentacja danych
Histogram for dk
100
frequency
80
60
40
20
0
0
3
6
9
dk
12
15
18
Graficzna prezentacja danych
polygon
100
frequency
80
60
40
20
0
0
3
6
9
dk
12
15
18
Po co rozkłady?
• Niekiedy konieczne jest załoŜenie, Ŝe
badana cecha posiada określony rozkład
– np. moŜemy załoŜyć, Ŝe rozkład cechy
„gęstość drewna” jest zgodny z rozkładem
normalnym i wykorzystać później tę
informację do estymacji, testowania hipotez
lub modelowania
Po co rozkłady?
• Stwierdzenie zgodności cechy z danym
rozkładem pozwala na zrozumienie
zaleŜności istniejących w zbiorze danych
• W takiej sytuacji zwykle buduje się rozkład
teoretyczny na bazie danych pomiarowych
i porównuje otrzymane rozkłady
Po co rozkłady?
• Do dopasowania rozkładów stosuje się
zwykle metodę momentów lub metodę
największej wiarygodności
• Rozkłady teoretyczne są podstawą wielu
metod statystycznych (estymacji, testów,
...), stąd konieczne jest sprawdzenie, czy
dane mają rozkład zgodny np. z
rozkładem normalnym
Typy zmiennych
• Jakościowe (określające przynaleŜność do
określonej grupy lub kategorii, np. płeć,
kolor, gatunek drewna, ...0
• Ilościowe (moŜliwe do pomierzenia z
wykorzystaniem skali pomiarowych, dla
których moŜliwe jest dodawania czy
uśrednianie, np. miąŜszość kłody, gęstość
drewna, ...)
Zmienna a typ rozkładu
• JeŜeli zmienna ma postać skończonego
zbioru - jest to zmienna skokowa (np.
wiek, klasa grubości, ...) moŜliwa do
opisania rozkładem
prawdopodobieństwa
Zmienna a typ rozkładu
• JeŜeli zmienna moŜe przyjąć dowolna
wartość (lub dowolną wartość z
określonego przedziału) - mówimy o
zmiennej ciągłej (np. długość, grubość,
...) moŜliwej do opisania gęstością
prawdopodobieństwa
Zmienna a typ rozkładu
• W wielu przypadkach (z powodu
technicznych ograniczeń pomiarów lub z
powodów praktycznych) zmienne ciągłe
traktowane są ja dyskretne (np. kiedy
grubość mierzona jest z zaokrągleniem do
1mm czy długość do 1cm)
Przykładowe rozkłady
• Rozkład Beta uŜywany jest do
modelowania rozkładów wielkości
uporządkowanych, mających naturalny
limit dolny i górny
• Rozkład dwumianowy uŜywany jest do
opisu takich zjawisk, jak np. liczba K/M czy
liczba elementów wadliwych w próbie
złoŜonej z n elementów pobranych z
populacji
Przykładowe rozkłady
• Rozkład chi-kwadrat uŜywany jest do
modelowania zmiennych reprezentujących
częstości
• Rozkład wykładniczy uŜywany jest często
do modelowania czasu między
zdarzeniami
• Rozkład Poisson’a uŜywany jest do
modelowania zjawisk rzadkich
Przykładowe rozkłady
• Rozkład normalny jest najczęściej
stosowany w estymacji statystycznej
• Rozkład Weibull’a stosuje się często do
modelowania czasu, który mija do
momentu wystąpienia awarii
• ...
Rozkład normalny
• Najczęściej stosowany rozkład w
statystyce
• Podstawa wielu metod statystycznych:
estymacji, testów, regresji, korelacji,
analizy wariancji, ...
Rozkład normalny
• Opisuje zmienne, które mogą przybierać
postać nieskończonej liczby niezaleŜnych
zdarzeń losowych
• Przykład rozkładu zmiennej ciągłej
• Jego funkcję gęstości
prawdopodobieństwa moŜna opisać
następująco:
Rozkład normalny
• gdzie:
– x - zmienna
– µ - średnia arytmetyczna
– σ - odchylenie standardowe
Rozkład normalny
Własności (r-d normalny)
• Wartość funkcji gęstości rośnie dla x<µ i
maleje dla x>µ
• Funkcja gęstości ma maksimum w punkcie
x=µ
• Wartość oczekiwana zmiennej X wynosi
E(X)=µ
• Wariancja zmiennej X równa jest D2X =
σ2
Własności (r-d normalny)
• dla x = µ funkcja gęstości ma wartość
• rozkład ma 2 punkty przegięcia dla x=µ σix=µ+σ
• rozkład normalny jest symetryczny, a oś
symetrii zdefiniowana jest jako x = µ
Własności (r-d normalny)
• Im wariancja / odchylenie standardowe
jest mniejsze, tym funkcja gęstości jest
węŜsza
• funkcja prawdopodobieństwa jest całką z
funkcji gęstości prawdopodobieństwa
Własności (r-d normalny)
Standaryzowany r.n.
• KaŜdy rozkład normalny moŜe być
znormalizowany, tj. doprowadzony do
postaci rozkładu o średniej 0 i odchyleniu
standardowym 1: N(0,1).
• Wartość oczekiwana standaryzowanego rdu normalnego równa jest zero (EZ = 0) a
odchylenie standardowe równe jest 1 (D2Z
= 1).
Standaryzowany r.n.
• Standaryzacja to zamiana zmiennej x na
z, gdzie:
• Funkcja gęstości prawdopodobieństwa tej
funkcji:
Standaryzowany r.n.
Własności (r-d normalny)
• Pomiędzy µ - σ i µ + σ znajduje się około
68% wszystkich wartości zmiennej
• W przedziale od µ - 2*σ do µ + 2*σ jest
około 95% wszystkich wartości zmiennej
• W przedziale od µ - 3*σ do µ + 3*σ mamy
około 99,7% wszystkich obserwacji
Rozkład skumulowany
cumulative histogram
frequency
250
200
150
100
50
0
0
3
6
9
dk
12
15
18
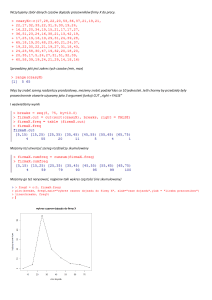
Rozkład skumulowany
Rozkład skumulowany
Rozkład skumulowany
Rozkład skumulowany
Rozkład dwumianowy
• Przykład funkcji rozkładu
prawdopodobieństwa
• Opisuje prawdopodobieństwo uzyskania k
sukcesów w n niezaleŜnych próbach,
gdzie prawdopodobieństwo sukcesu w
jednej próbie wynosi p
Rozkład dwumianowy
Rozkład dwumianowy
Własności (r-d dwum.)
• Wykres funkcji rozkładu jest symetryczny
dla p = 0.5
• dla p < 0.5 rozkład jest skośny dodatnio
• dla p > 0.5 rozkład jest skośny ujemnie
Własności (r-d dwum.)
• Wartość oczekiwana E(X) = n * p
• Wariancja D2X = n p q
• Odchylenie standardowe
Dziekuje za uwagę!