Wykład 1

Wykład 1
Pojęcie funkcji, nieskończone ciągi liczbowe, dziedzina funkcji, wykres funkcji, funkcje
elementarne, funkcje złożone, funkcje odwrotne.
1.1 Funkcje
Definicja 1.1.
Mówimy, że w zbiorze liczb X jest określona pewna funkcja f, (funkcja jednej zmiennej),
jeżeli każdej liczbie x ze zbioru X jest przyporządkowana dokładnie jedna liczba y pewnego
zbioru liczb Y. (rys. 1.1)
Przyporządkowanie to zapisujemy w postaci:
(l)
y= f (x).
 Zmienną x we wzorze (l) nazywamy
argumentem funkcji lub zmienną niezależną,
zmienną y - zmienną zależną.
 Określoną liczbę X0 ze zbioru X nazywamy
wartością argumentu funkcji f albo wartością
zmiennej niezależnej x a przyporządkowaną jej
liczbę y0 ze zbioru Y nazywamy wartością
funkcji f w punkcie X0.
 Zbiór X wartości argumentów funkcji f
nazywamy dziedziną funkcji f.
Rys. 1.1
Funkcja.
 Zbiór Y wartości funkcji f nazywamy zbiorem wartości funkcji f, lub
przeciwdziedziną tej funkcji.
Niekiedy, dla zaznaczenia, że funkcja f przekształca elementy zbioru X na elementy zbioru Y
używa się notacji:
f: X  Y
Każda funkcja jest przyporządkowaniem jednoznacznym, tzn. jednemu argumentowi funkcji
odpowiada jedna wartość. Jeśli ponadto każdej wartości odpowiada jeden argument, to taką
funkcję nazywamy wzajemnie jednoznaczną.
Przykłady funkcji:
f(x)=x2, f(x)= (x+1)/(x-2), f(x)=sin x. Określić ich dziedzinę i przeciwdziedzinę.
Przykłady przyporządkowań, które nie są funkcjami:
y2=x, y2+x2=25.
Przykłady:
Określić dziedzinę następujących funkcji:
y  x  3 , y  ln x  5
x  3x  2 są równe?
Czy funkcje y  x  3 i y 
x  2
1
Wykresem funkcji y = f(x) nazywamy
umieszczony w układzie współrzędnych
kartezjańskich zbiór punktów o
współrzędnych (x, f(x)).
Rysunek obok przedstawia wykres funkcji
f ( x)  x  1 .
D = 1, ∞).
1.2 Ciągi nieskończone.
Definicja 1.2.
Ciąg nieskończony jest funkcją, której dziedziną jest zbiór liczb naturalnych.
Dla wygody ciąg nieskończony będziemy nazywać po prostu ciągiem.
Jeśli f jest ciągiem nieskończonym, to każdej liczbie naturalnej n odpowiada liczba
rzeczywista f(n). Liczby te mogą być zapisane w sposób następujący:
f(1), f(2), f(3), …, f(n), …
f(n) nazywane jest n-tym wyrazem ciągu lub ogólnym wyrazem ciągu.
Niekiedy wygodnie jest zapisać ciąg w postaci sekwencji liczb rzeczywistych:
{an} = a1, a2, a3, … ,an, …
gdzie an = f(n).
Definicja 1.3.
Dwa ciągi:
a1, a2, a3, … ,an, …
oraz
b1, b2, b3, … ,bn, …
są równe wtedy i tylko wtedy, gdy ai = bi dla każdej dodatniej całkowitej liczby i.
Przykład 1.1
Napisać pierwsze cztery oraz dziesiąty wyraz ciągu o następującym wyrazie ogólnym:
n
n2
a) a n 
,
c) a n  ( 1) n 1
,
n 1
3n  1
b) a n  2  (0,1) n ,
d) an  4
2
Definicja 1.4.
Mówimy, że ciąg {an} ma granicę L , co zapisujemy w postaci
lim a n  L
n
jeśli dla każdej liczby rzeczywistej  > 0 istnieje dodatnia liczba naturalna N taka, że dla
każdego n > N zachodzi
an  L  
Jeśli lim a n nie istnieje w sensie
n
definicji 1.4., to mówimy, że ciąg
{an} nie ma granicy, lub że jest
rozbieżny.
Interpretacja geometryczna:
Każdy wyraz ciągu {an} może
być przedstawione w układzie
współrzędnych jako punkt o
współrzędnych (k, ak) k = 1, 2,
…. (rys. 1.2). Jeżeli lim a n  L ,
n
to dla każdego  > 0 możemy
Rys. 1.2
dobrać taką wartość n, że punkt
Interpretacja geometryczna ciągu zbieżnego.
(n, an) i wszystkie następne
punkty leżą pomiędzy liniami y = L +  i y = L - .
Definicja 1.5
Określenie lim a n   oznacza, że dla dowolnej liczby rzeczywistej P istnieje taka liczba
n 
naturalna N, że an > P dla każdego n > N .
Definicja 1.6
Określenie lim a n   oznacza, że dla dowolnej liczby rzeczywistej P istnieje taka liczba
n 
naturalna N, że an < P dla każdego n > N .
Twierdzenie 1.1
1. Jeśli r  1 , to lim r n  0
n
2. Jeśli r  1 , to lim r n   .
n 
3
Przykład 1.2
Napisać pierwsze cztery wyrazy i znaleźć granice, jeśli istnieją, ciągów:
 2  n 
1.    
 3  
2.
1,01 
n
Twierdzenie 1.2
Jeśli lim a n  L oraz lim bn  M , to:
n
n 
lim (a n  bn )  L  M ,
n 
lim a n bn  LM ,
n 
an
L
, jeśli M ≠ 0 i bn ≠ 0 dla każdego n.

n  b
M
n
lim
Twierdzenie 1.3
c
  .
n  a
n
Jeśli lim a n  0 to, dla dowolnej stałej c, lim
n 
c
0
n a
n
Jeśli lim a n   , to lim
n
Twierdzenie 1.4
Niech
Wn(x) = anxn + an-1xn-1 + … + a1x + a0,
Wm(x) = bmxm + bm-1xm-1 + … + b1x + b0
Wówczas
  gdy n  m
W ( x)  an
lim n

gdy n  m
n  W ( x )
m
 bm
 0 gdy n  m
Przykład 1.3
Znajdź granicę ciągu o wyrazie ogólnym an 
2n
.
5n  3
Przykład 1.4
Znajdź granicę ciągu o wyrazie ogólnym an  4n 2  5n  7  2n .
4
Twierdzenie 1.5
an

1
lim 1    e , przy czym lim a n   i an  0. Liczba e jest podstawą logarytmu
n 
n
 an 
naturalnego, e  2,71828.
Przykład 1.5
n
 4
Obliczyć lim 1   .
n
 n
Rozwiązanie
4
n


4
1
 4


4

lim 1    lim 1 
  e
n
n

 n / 4  
 n


n
5
Funkcje elementarne.
1. Funkcja wielomianowa.
y = anxn + an-1xn-1 + … + a3x3 + a2x2 + a1x
+ a0
D=R
Zbiór wartości Y zależy od stopnia
wielomianu.
Przykłady:
y=a
funkcja stała
Y = {a}
y = a1x +a0
funkcja liniowa
Y=R
6
y = a2x2 + a1x + a0
Funkcja kwadratowa
D=R
  yw , ), a2  0
Y 
(, yw , a2  0
2. Funkcja wymierna
an x n  an1 x n1  ...  a2 x 2  a1 x  a0
bm x m  bm1 x m1  ...  b2 x 2  b1 x  b0
D – wszystkie liczby rzeczywiste, które
nie są pierwiastkami mianownika.
Y zależy od postaci funkcji wymiernej.
y
7
3. Funkcja wykładnicza
y = ax a>0 a ≠ 1
Y = (0, ∞)
Jeśli a > 1, to funkcja jest rosnąca,
Jeśli a < 1, to funkcja jest malejąca.
4. Funkcja logarytmiczna
y = loga x D = (0, ∞), Y = R
a  (0, 1) (1, )
Jeśli a > 1, to funkcja jest rosnąca,
Jeśli a < 1, to funkcja jest malejąca.
8
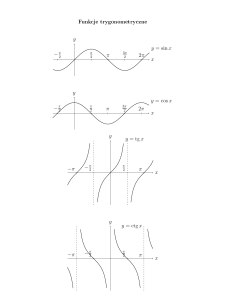
5. Funkcje trygonometryczne.
y = sin x D = R, Y = -1, 1
y = cos x D = R, Y = -1, 1
y = tg x D = {x: x  R i x ≠ k /2, k = ±1, ±2, …} , Y = R
9
y = ctg x D = {x: x  R i x ≠ k , k = ±1, ±2, …} , Y = R
Funkcja złożona
Niech dane będą dwie funkcje: g: A → B i f: B → C
Funkcję h określoną wzorem
h(x)= f(g(x)) nazywamy funkcja złożoną. Jej dziedziną jest dziedzina funkcji g,
natomiast zbiorem wartości jest zbiór wartości funkcji f.
Możemy zatem napisać h: A → C.
Funkcję g(x) nazywamy funkcją wewnętrzną a f(x) funkcją zewnętrzną.
Przykłady funkcji złożonych:
3
1
y  x  3 , y  sin x 2  5 , y  sin x 2 , y  sin 2 x , y 
, y  x2  5
3x  2




10
Funkcja odwrotna
Jeżeli funkcja f: X → Y jest wzajemnie jednoznaczna, tzn. każdej wartości odpowiada
dokładnie jeden argument, to istnieje wzajemnie jednoznaczna funkcja g odwrotna do
f, tzn. taka, że:
g: Y → X
oraz dla każdej pary liczb aX i bY jeżeli b = f(a), to a = g(b).
Funkcję odwrotną do y = f(x) oznaczamy symbolem y = f -1(x).
Jeśli dany jest wzór funkcji f, to aby otrzymać wzór funkcji f -1 wystarczy wyliczyć x
w zależności od y i zamienić nazwy zmiennych.
Przykłady:
Znaleźć funkcje odwrotne do:
1. y = x2 dla x ≥ 0
2.
y = 3x +5
Rozwiązanie
1. y  x 2  x 
y
Zamieniamy nazwy zmiennych i otrzymujemy wzór funkcji odwrotnej w
postaci y  x .
y 5
2. y  3x  5  y  5  3x  x 
3
Zamieniamy nazwy zmiennych i otrzymujemy wzór funkcji odwrotnej w
x5
postaci y 
.
3
Wykres funkcji odwrotnej otrzymujemy z
wykresu funkcji danej przez symetrię
względem prostej y = x.
Przykłady cd.
Funkcją odwrotną do y = ex , D = R, Y = (0,
y = lnx, D = (0, ∞), Y = R.
∞),
11
12
2.00
Funkcje cyklometryczne
y=arcsinx
Funkcją odwrotną do y = sin x, w
przedziale -/2, /2 jest
y = arcsin x,
D = -1, 1, Y = -/2, /2
1.00
y=sinx
0.00
-2.00
Funkcją odwrotną do y = cos x, w
przedziale 0,  jest
y = arccos x,
D = -1, 1, Y = 0, 
-1.00
0.00
1.00
2.00
4.00
-1.00
3.00
y=arccos x
-2.00
2.00
1.00
Funkcją
odwrotną
do y = tg
x, w
0.00
przedziale -1.00
0.00
(-/2, /2)
jest y =
-1.00
arctg x,
D = (-∞, ∞), Y = (-/2, /2)
10.00
y=tg x
5.00
y=arctg x
0.00
-10.00
-5.00
0.00
-5.00
5.00
1.00
2.00
3.00
4.00
y=cos x
10.00
Funkcją odwrotną do y = ctg x, w przedziale (0, )
jest y = arcctg x,
D = (-∞, ∞), Y = (0, )
-10.00
13